大二上 数据结构与算法 课堂模板算法 20241225
数据结构与算法
笔记主体部分来源于戚俊涵先生,在此表示感谢!
1-基本数据结构
2-分治策略
3-堆
4-排序
5-选择 & 树
6-搜索树 & 散列表 & 并查集
6.1-搜索树
6.2-散列表
unordered_map 是 C++ 标准模板库(STL)中的一个关联容器,它存储键值对(Key-Value Pair),并且基于哈希表实现。与 map 不同,unordered_map 不保证元素的顺序,但通常能提供更快的查找速度。下面我将结合简单例子为你讲解 unordered_map 的使用。
1. 包含头文件
要使用 unordered_map,首先需要包含对应的头文件:
#include <unordered_map>
2. 声明和初始化
unordered_map 可以存储任意类型的键和值,但键必须是唯一的。下面是一个简单的声明和初始化的例子:
#include <iostream>
#include <unordered_map>
using namespace std;
int main() {
// 声明一个unordered_map,键为string,值为int
unordered_map<string, int> ageMap;
// 插入键值对
ageMap["Alice"] = 30;
ageMap["Bob"] = 25;
ageMap["Charlie"] = 35;
// 使用insert方法插入键值对
ageMap.insert(make_pair("David", 40));
// 初始化时直接插入多个键值对
unordered_map<string, int> anotherMap = {
{"Eve", 28},
{"Frank", 22}
};
return 0;
}
3. 查找元素
可以使用 find 方法查找特定键的元素,如果找到,返回指向该元素的迭代器;如果未找到,返回指向 unordered_map 结尾的迭代器。也可以直接使用下标运算符 [] 访问元素,如果键不存在,会自动插入一个默认值的键值对。
#include <iostream>
#include <unordered_map>
using namespace std;
int main() {
unordered_map<string, int> ageMap = {
{"Alice", 30},
{"Bob", 25},
{"Charlie", 35}
};
// 使用find方法查找
auto it = ageMap.find("Bob");
if (it != ageMap.end()) {
cout << "Bob's age is " << it->second << endl;
} else {
cout << "Bob not found" << endl;
}
// 使用下标运算符访问
cout << "Alice's age is " << ageMap["Alice"] << endl;
// 如果键不存在,会插入一个默认值的键值对
cout << "New person's age is " << ageMap["New person"] << endl; // 默认值为0
return 0;
}
4. 遍历元素
可以使用范围基于的 for 循环(C++11 及以后版本)或迭代器来遍历 unordered_map 中的所有元素。
#include <iostream>
#include <unordered_map>
using namespace std;
int main() {
unordered_map<string, int> ageMap = {
{"Alice", 30},
{"Bob", 25},
{"Charlie", 35}
};
// 使用范围基于的for循环遍历
for (const auto& pair : ageMap) {
cout << pair.first << " is " << pair.second << " years old" << endl;
}
// 使用迭代器遍历
for (auto it = ageMap.begin(); it != ageMap.end(); ++it) {
cout << it->first << " is " << it->second << " years old" << endl;
}
return 0;
}
5. 删除元素
可以使用 erase 方法删除特定键的元素,也可以删除迭代器指向的元素。
#include <iostream>
#include <unordered_map>
using namespace std;
int main() {
unordered_map<string, int> ageMap = {
{"Alice", 30},
{"Bob", 25},
{"Charlie", 35}
};
// 删除特定键的元素
ageMap.erase("Bob");
// 使用迭代器删除元素
auto it = ageMap.find("Charlie");
if (it != ageMap.end()) {
ageMap.erase(it);
}
// 遍历剩余元素
for (const auto& pair : ageMap) {
cout << pair.first << " is " << pair.second << " years old" << endl;
}
return 0;
}
6. 统计元素数量
可以使用 size 方法获取 unordered_map 中的元素数量,使用 empty 方法判断是否为空。
#include <iostream>
#include <unordered_map>
using namespace std;
int main() {
unordered_map<string, int> ageMap = {
{"Alice", 30},
{"Bob", 25},
{"Charlie", 35}
};
cout << "Number of elements: " << ageMap.size() << endl;
ageMap.clear(); // 清空unordered_map
if (ageMap.empty()) {
cout << "The map is empty" << endl;
}
return 0;
}
总结
unordered_map 是一个非常有用的容器,适用于需要快速查找、插入和删除元素的场景。通过上述例子,你可以看到如何声明、初始化、查找、遍历、删除和统计 unordered_map 中的元素。
6.3-并查集
int find(int x) //查找父节点
{
if(pre[x] == x) return x;
return pre[x] = find(pre[x]);
}
void join(int x,int y) //合并
{
int fx=find(x), fy=find(y);
if(fx != fy)
pre[fx]=fy;
}
7-图
7.1-BFS(邻接表)
vector<vector<int>> graph; // 图的邻接表表示
vector<int> color; // 访问标记数组
void BFS(int start)
{
queue<int> q; // BFS队列
q.push(start); // 将起始节点加入队列
color[start] = 1; // 标记起始节点为已访问
while (!q.empty())
{
int current = q.front(); // 取出队列的第一个元素
q.pop(); // 将该元素从队列中移除
color[current] = 2;
// 遍历当前节点的所有邻接节点
for (auto &neighbour:graph[current])
{
color[neighbour] = 1;
q.push(neighbour);
}
}
}
7.2-DFS(邻接表)
vector<vector<int>> graph; // 图的邻接表表示
vector<int> color; // 访问标记数组
void DFS(int node)
{
color[node] = 1;
for (auto &neighbour : graph[node])
{
if (color[neighbour]==0)
{
DFS(neighbour);
}
}
color[node] = 2;
}
8-深度优先算法&生成树
- DAG:有向无环图
- (S)CC:(强)连通图
- MST:最小生成树
8.1-Topological Sort(DAG)
//拓扑序:DAG中的所有顶点的线性序列,且满足每个顶点出现且只出现一次;若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面
int V; //顶点个数
vector<vector<int>> graph;
vector<int> indegree;
queue<int> q; // 维护一个入度为0的顶点的集合
bool topological_sort()
{
for(int i=0; i<V; ++i)
if(indegree[i] == 0)
q.push(i); // 将所有入度为0的顶点入队
int count = 0; // 计数,记录当前已经输出的顶点数
while(!q.empty())
{
int current = q.front(); // 从队列中取出一个顶点
q.pop();
cout << current << " "; // 输出该顶点
count++;
// 将所有current指向的顶点的入度减1,并将入度减为0的顶点入栈
for(auto &node:graph[current])
{
indegree[node]--;
if(indegree[node]==0)
q.push(node);
}
}
if(count < V)
return false; // 没有输出全部顶点,有向图中有回路
else
return true; // 拓扑排序成功
}
8.2-Minimum Spanning Trees
8.2.1-Kruskal算法
int V; //顶点个数
int parent[MAX]; //定义parent数组用来判断边与边是否形成环路
struct Edge
{
int u,v,w;
};
vector<Edge> edges;
bool cmp(Edge a,Edge b)
{
return a.w < b.w;
}
int Find(int x)
{
return parent[x]==x ? x : parent[x] = find(parent[x]);
}
void Kruskal()
{
sort(edges.begin(),edges.end(),cmp); //把图中的所有边按代价从小到大排序
for(int i=0;i<V;i++) //把图中的n个顶点看成独立的n棵树组成的森林
parent[i] = i;
for(int i=0;i<edges.size();i++)
{
int u=edges[i].u,v=edges[i].v;
if(Find(u)!=Find(v)) //如果Find(u)=Find(v),则形成环路
//将此边的结尾顶点放入下标为起点的parent数组中,表示此顶点已经在生成树集合中
parent[Find(u)] = Find(v);
}
}
8.2.2-Prim算法
#define inf INT_MAX
int n; //顶点个数
int res; //结果
vector<vector<int>> ma(n+1,vector<int>(n+1,inf)); //邻接矩阵,存边权,初始化为正无穷
vector<int> dist(n+1,inf); //dist[]储存到生成树的距离
vector<bool> book(n+1,false); //用book数组记录某个点是否加入到生成树中
void prim()
{
dist[1] = 0;
book[1] = true;
for(int i = 2; i <= n; i++)
dist[i] = min(dist[i],ma[1][i]);//用点1去更新dist[]
for(int i = 2; i <= n; i++)
{
int temp = inf;//初始化距离
int t = -1; //接下来去寻找离生成树点集最近的点加入到集合中,用t记录这个点的下标。
for(int j = 2 ; j <= n; j++)
{
if(!book[j] && dist[j]<temp)
{
temp = dist[j];
t = j;
}
}
//如果t==-1,意味着在集合V找不到边连向集合S,生成树构建失败,将res赋值正无穷表示构建失败
if(t==-1)
{
res = INF;
return;
}
book[t] = true;//如果找到了这个点,就把它加入集合S
res += dist[t];//加上这个点到集合S的距离
for(int j = 2 ; j <= n ; j++)
dist[j] = min(dist[j],ma[t][j]);//用新加入的点更新dist[]
}
8.2.3-Borůvka算法
int N,M;//N:点个数,M:边条数
struct Edge
{
int u,v,w;
}
vector<Edge> edges;
vector<bool> visited(M+1,0);
vector<int> parent(N+1,0),dist(M+1,0),e(M+1,0);
int find(int x)
{
return parent[x] == x ? x : parent[x] = find(parent[x]);
}
bool cmp(Edge a,Edge b)
{
return a.w < b.w;
}
int boruvka()
{
int cnt = 0,sum = 0;
for(int i = 1;i <= N; i++)
parent[i] = i;
while (1)
{
int cnt_tmp=0;
memset(dist,inf,sizeof(dist)); //初始化dist数组
for (int i = 1; i <= M; i++) //每个边都计算一下dist
{
int f1 = find(edges[i].u),f2 = find(edges[i].v);//用并查集找到根
if (f1 == f2 || visited[i]) //如果一棵树或者拓展过这个边
continue;
cnt_tmp++; //记录一下看下有没有边可以拓展
if (edges[i].w < d[f1])
dist[f1] = edges[i].w,e[f1] = i; //更新,e数组表示dist数组对应的边
if (edges[i].w < d[f2])
dist[f2] = edges[i].w,e[f2] = i;
}
if (cnt_tmp == 0 || cnt == n - 1)
break;
for (int i = 1; i <= N; i++) //扫描每棵树
{
int f1 = find(edges[e[i]].u),f2 = find(edges[e[i]].v);
if(dist[i] == inf || f1 == f2 || visited[e[i]])
continue;
visited[e[i]] = 1; //加入最小生成树集合
parent[f1] = f2;
sum += edges[e[i]].w;
cnt++;
}
}
}
9-贪心
略
10-最短路
10.1-Floyd算法
1,从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
2,对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是更新它。
把图用邻接矩阵G表示出来,如果从Vi到Vj有路可达,则G[i][j]=d,d表示该路的长度;否则G[i][j]=无穷大。定义一个矩阵D用来记录所插入点的信息,D[i][j]表示从Vi到Vj需要经过的点,初始化D[i][j]=j。把各个顶点插入图中,比较插点后的距离与原来的距离,G[i][j] = min( G[i][j], G[i][k]+G[k][j] ),如果G[i][j]的值变小,则D[i][j]=k。在G中包含有两点之间最短道路的信息,而在D中则包含了最短通路径的信息。
比如,要寻找从V5到V1的路径。根据D,假如D(5,1)=3则说明从V5到V1经过V3,路径为{V5,V3,V1},如果D(5,3)=3,说明V5与V3直接相连,如果D(3,1)=1,说明V3与V1直接相连。
int N; //顶点个数
vector<vector<int>> ma;//邻接矩阵,存储i到j的边权
void Floyd()
{
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
for (int k = 0; k < N; k++)
{
if (ma[j][k] > ma[j][i] + ma[i][k]) //若j到k间存在更短的通路,则更新
ma[j][k] = ma[j][i] + ma[i][k];
}
}
}
}
10.2-Dijkstra算法
#define inf INT_MAX
template <typename T>
using min_priority_queue = priority_queue<T, vector<T>, greater<T>>;
class node
{
public:
int dist = inf;
vector<pair<node *, int>> edges;
bool operator>(node *&n) { return dist > n->dist; }
};
min_priority_queue<node *> Q;
void Dijkstra(vector<node *> &nodes, int s)
{
nodes[s]->dist = 0;
Q.push(nodes[s]);
while (!Q.empty())
{
node *u = Q.top();
Q.pop();
for (auto tmp : u->edges)
{
node *v = tmp.first;
if (v->dist > u->dist + tmp.second)
{
v->dist = u->dist + tmp.second;
Q.push(v);
}
}
}
}
10.3-Bellman-Ford算法
//用于判断图中是否存在负权环
#define inf INT_MAX
int N,M;//N:顶点个数,M:边条数
struct Edge
{
int u, v, w;
};
vector<Edge> edges(M+1);
vector<int> dist(N+1,inf);
bool Bellman_Ford()
{
for (int i = 1; i <= N; i++) //将dist数组更新一次,存储i节点所在环的权
{
for (int j = 1; j <= M; j++)
{
int u = edges[j].u, v = edges[j].v, w = edges[j].w;
if (dist[v] > dist[u] + w)
dist[v] = dist[u] + w;
}
}
for (int i = 1; i <= M; i++) //再次更新dist数组,若权值改变,则图中存在负权环
{
if (dis[edges[i].v] > dis[edges[i].u] + edges[i].w)
return 1;
}
return 0;
}
11-动态规划
11.1钢材切割问题
一种解决该问题的dp算法如下:
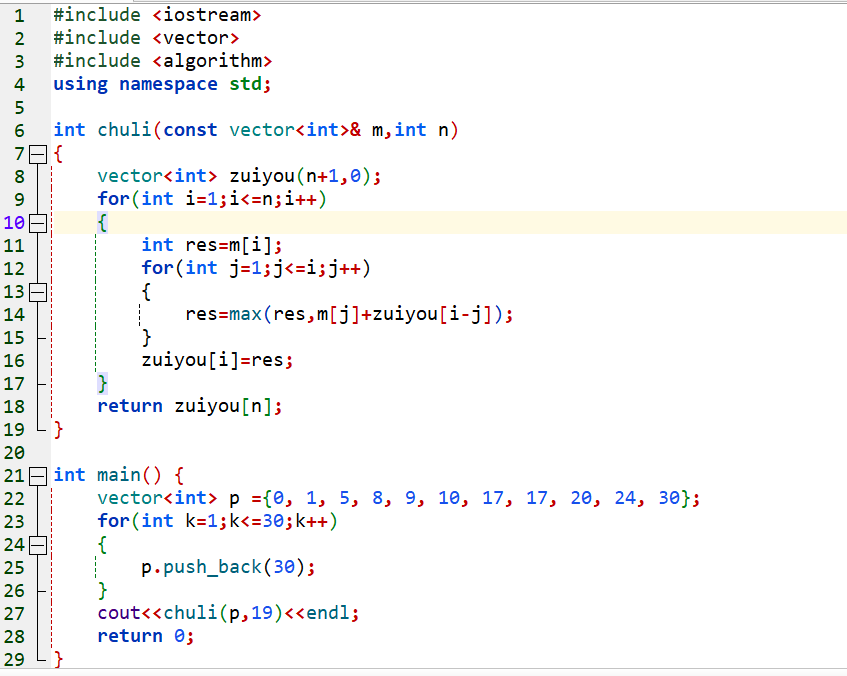
//对于一段长度为n的绳子,有一个数组vector
include <bits/stdc++.h>
using namespace std;
int main(){
vector
vector
//dp可以看作是一种自下而上的思考方式,计算出最优子结构,然后把最优子结构结合起来,就会成为整体最优.
//因而,很多dp的计算就是,先求出基础情况,如dp[0],dp[i][0],然后用0求1,用1求2,用n-1求n.
//这个求的方程,我们叫做动态转移方程,这里指的就是dp[i]=max(value[j]+dp[i-j],0<=j<=i)
dp[0]=0;
for(int i=1;i<value.size();i++){
int maxValue=value[i];
for(int j=0;j<=i;j++)
maxValue=max(maxValue,value[j]+dp[i-j]);
dp[i]=maxValue;
}
cout<<dp[value.size()-1];
}
11.2最小编辑距离
//最小编辑距离
//这个挺经典的.leetcode72,或者去看【ACM 金牌选手教你动态规划的本质。力扣 No.72 编辑距离,真·动画教编程,适合语言初学者或编程新人。】 https://www.bilibili.com/video/BV1FJ4m1M7RJ/?share_source=copy_web&vd_source=3ce6749836b98dddde11ab8e5277b8ea
include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int minDistance(string word1, string word2) {
vector<vector
for(int i=0;i<=word1.size();i++)
dp[i][0]=i;
for(int i=0;i<=word2.size();i++)
dp[0][i]=i;
for(int i=1;i<=word1.size();i++){
for(int j=1;j<=word2.size();j++){
if(word1[i-1]!=word2[j-1]){
int minIndex=min(dp[i-1][j],dp[i][j-1]);
dp[i][j]=min(minIndex,dp[i-1][j-1])+1;
} else
dp[i][j]=dp[i-1][j-1];
}
}
return dp[word1.size()][word2.size()];
}
};
11.3矩阵相乘问题
include <bits/stdc++.h>
using namespace std;
//对于给定的n个矩阵进行相乘,求花销最小的结合方式.
//意思是:比方说矩阵A1,是q1q2的长和宽,A2是q2q3的长和宽,A3是q3q4的长和宽,每次相乘(例如An-1An)的花销是qn-1qnqn+1,矩阵的乘法满足结合律,这里的计算就是,如何通过结合律,求出最小的开销.
int main(){
vector
int n=cost.size()-1;
vector<vector
for(int i=0;i<n;i++)
dp[i][i]=0;
for(int i=0;i<n;i++){
for(int j=i+1;j<n;j++){
dp[i][j]=cost[i]cost[i+1]*cost[i+2];
}
}//dp基础状态的标记
//接下来就是要求动态转移方程
//应该去想的是,求出Ai*Ai+1*...*Aj的最小花费,就是求Ai*Ai+1*...*Ak的花费+Ak+1*Ak+2*...*Aj的花费+cost[i]*cost[k+1]*cost[j+1]的最小花费(为什么?就是把一个比较大的乘法在k处拆分成两个乘法.)
//所以就可以求出动态转移方程.
//按照我们自下而上,先求最优子结构的角度来考虑,首先要计算的,肯定是Ai*Ai+1的最小花费,然后再求每三个一结合的最小花费,再求多个的.
//因而dp的求的顺序如下:
for (int l=1;l<n;l++) {
for(int i=0;i+l<n;i++){
int minCost=INT_MAX;
for(int k=i;k<i+l;k++)
minCost=min(minCost,dp[i][k]+dp[k+1][i+l]+cost[i]*cost[k+1]*cost[i+l+1]);
dp[i][i+l]=minCost;
}
}
for(int i=0;i<n;i++){
for(int j=i;j<n;j++)
cout<<dp[i][j]<<' ';
cout<<endl;
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号