[dp 记录] CF856D Masha and Cactus

\(\texttt{link}\)

首先对于一条边 \((u,v,w)\)，记 \(l = lca(u,v)\)，若选择了这条边，则树上 \(u\rightarrow v\) 的路径上的边都不可以再出现在选的其他边的路径上。

记 \(dp(u)\) 为子树 \(u\) 内合法选边且所选的路径均在子树 \(u\) 内的最大权值，则：

• 不选 \(lca = u\) 的边，则 \(dp(u) = \sum\limits_{fa_v = u}dp(v)\) ;

• 若选择了一条 \(lca = u\) 的边，则：

  

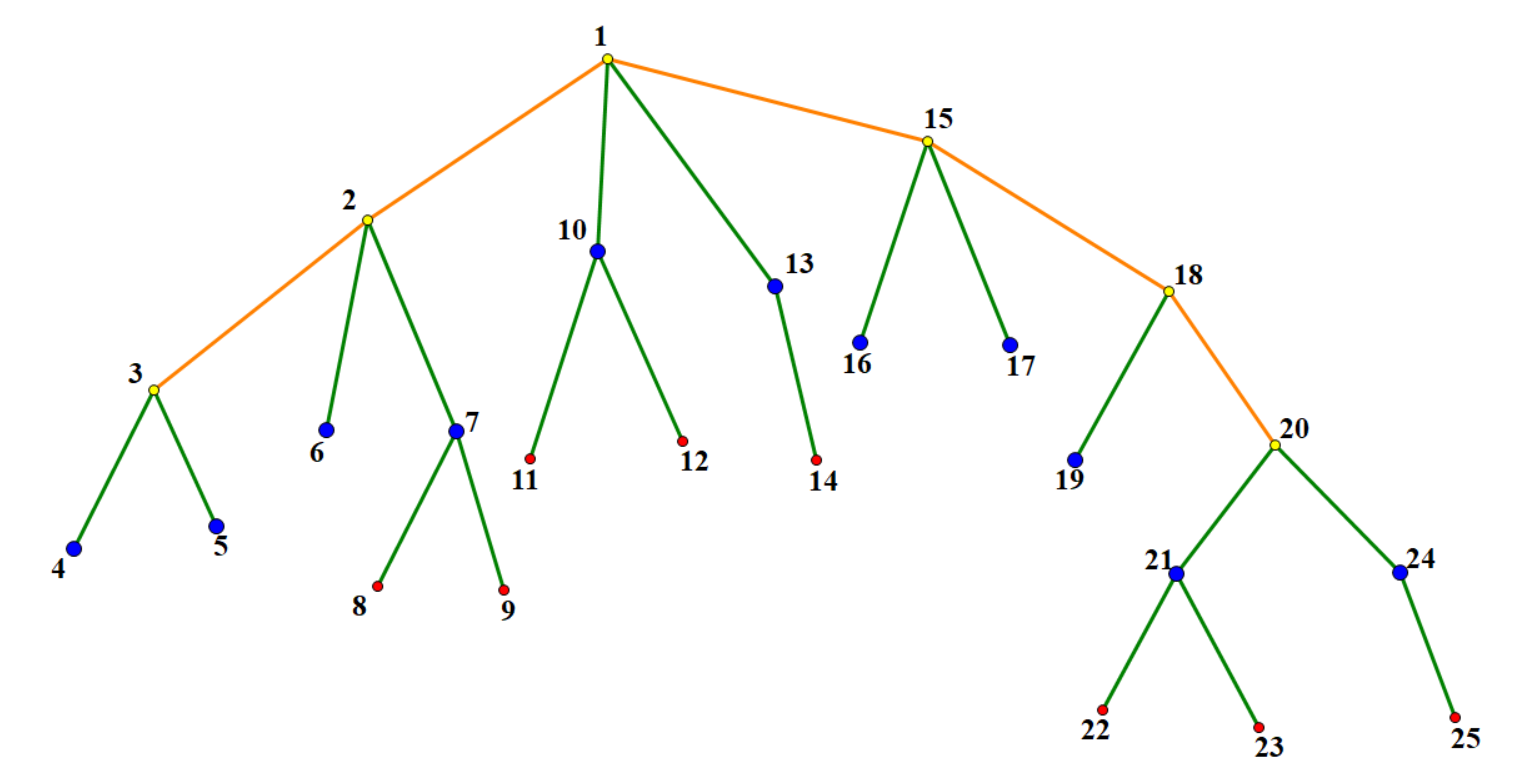
  (图源 https://www.cnblogs.com/ET2006/p/Codeforces-856D.html，侵删)

  \(dp(u) = \sum dp(\text{蓝色点}) + w\)，直接暴力求是 \(O(n^2)\) 的，（也许巧妙地）考虑记 \(g(u) = -dp(u) + \sum\limits_{fa_v = u}dp(v)\)，则有

  \[dp(u) = \sum g(\text{除 u 外路径上的点}) + \sum\limits_{fa_v = u}dp(v) + w \]

于是搞个线段树维护一下 \(\sum g(\text{除 u 外路径上的点})\) 就做完了。

\(\texttt{Code:}\)

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5;
int n, m; vector<int> G[maxn];
int depth[maxn], s[maxn], fa[maxn], son[maxn], top[maxn], tot, id[maxn];
void dfs1(int u) {
    s[u] = 1; depth[u] = depth[fa[u]] + 1;
    for (int v : G[u]) {
        fa[v] = u; dfs1(v); s[u] += s[v];
        if (s[v] > s[son[u]]) son[u] = v;
    }
}
void dfs2(int u, int Top) {
    top[u] = Top; id[u] = ++tot;
    if (!son[u]) return;
    dfs2(son[u], Top);
    for (int v : G[u]) if (v ^ son[u]) dfs2(v, v);
}
int lca(int a, int b) {
    while (top[a] ^ top[b]) {
        if (depth[top[a]] < depth[top[b]]) swap(a, b);
        a = fa[top[a]];
    }return depth[a] < depth[b] ? a : b;
}
struct Edge {int u, v, w;};
vector<Edge> e[maxn];
int dp[maxn], t[maxn << 2];
void modify(int now, int l, int r, int x, int y) {
    t[now] += y;
    if (l == r) return;
    int mid = (l + r) >> 1;
    if (x <= mid) modify(now << 1, l, mid, x, y);
        else modify(now << 1 | 1, mid + 1, r, x, y);
}
int query(int now, int l, int r, int x, int y) {
    if (x <= l && r <= y) return t[now];
    int mid = (l + r) >> 1, res = 0;
    if (x <= mid) res = query(now << 1, l, mid, x, y);
    if (y > mid) res += query(now << 1 | 1, mid + 1, r, x, y);
    return res;
}
int ask(int a, int b) {
    int res = 0;
    while (top[a] ^ top[b]) {
        if (depth[top[a]] < depth[top[b]]) swap(a, b);
        res += query(1, 1, n, id[top[a]], id[a]);
        a = fa[top[a]];
    }if (depth[a] > depth[b]) swap(a, b);
    return res + query(1, 1, n, id[a], id[b]);
}
void dfs(int u) {
    for (int v : G[u]) dfs(v), dp[u] += dp[v];
    int mx = 0;
    for (Edge cur : e[u]) {
        mx = max(mx, ask(cur.u, cur.v) + cur.w);
    }dp[u] += mx; modify(1, 1, n, id[u], -mx);
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 2; i <= n; i++) {
        int u; scanf("%d", &u);
        G[u].push_back(i);
    }dfs1(1); dfs2(1, 1);
    for (int i = 1; i <= m; i++) {
        int u, v, w; scanf("%d%d%d", &u, &v, &w);
        e[lca(u, v)].push_back((Edge){u, v, w});
    }dfs(1); printf("%d", dp[1]);
    return 0;
}