做题记录

\(\bullet\) \(\texttt{ AGC006C Rabbit Exercise}\)

首先，对于操作 \(a_i=p\)，操作后 \(p\) 的期望坐标 \(x_p = \frac 1 2(2x_{p-1} - x_p) + \frac 1 2(2x_{p+1} - x_p) = x_{p-1} + x_{p+1} - x_p\)。

考虑差分，令 \(d_i = x_i - x{i - 1}\)，则操作完 \(a_i = p\)后，改变的 \(d\) 有：

\(\small\odot\) \(d_p = x_p - x_{p-1} = x_{p-1} + x_{p+1} - x_p - x_{p-1} = x_{p+1} - x_p = d_{p+1}\)

\(\small\odot\) \(d_{p+1} = x_{p+1} - (x_{p-1} + x_{p+1} - x_p) = x_p - x_{p-1} = d_p\)

实际效果为交换 \(d_p\) 和 \(d_{p+1}\)，于是就可以先做一轮 \(m\) 个操作，并将映射快速幂做 \(k\) 次即可。

时间复杂度 \(O(n \log k)\)

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ AGC044C Strange Dance}\)

考虑从低位到高位建一棵 0/1/2 trie。

对于 S 操作，在根节点打上 lazy tag，表示交换 1.2 这两棵子树；

对于 R 操作，从根节点出发，将 0 子树变成 1 子树，1 子树变成 2 子树，原先的 2 子树变成 0 子树，并递归新的 0 子树，这样的复杂度是 \(O(n)\) 的。

总复杂度 \(O(n |T|)\)。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ARC072E Alice in linear land}\)

对于 \(\forall i\in[1,n)\) ，先预处理出做=执行完 \([1,i]\) 的操作后与 \(D\) 的距离，记作 \(X_i\)。

对于询问 \(i\)，我们可以将 \(X_{q_i - 1}\) 修改成 \((0,X_{q_i - 1}]\)，问题就变成了：

是否存在一个数 \(x \in (0,X_{q_i - 1}]\) ，使得执行完 \((q_i + 1,n]\) 操作后 \(x\) 变成 \(0\)。

记 \(dp(i,x)\) 表示 \(x\) 执行完 \([i,n]\) 操作后能否变成 \(0\)，则有转移：

\[dp(i,x)=\begin{cases}dp(i+1,x) &x < \dfrac{d_i} 2 \\ dp(i+1,d_i - x) &\dfrac{d_i} 2\le x \le d_i \\ dp(i+1,x-d_i) &x > d_i \end{cases} \]

这样做是 \(O(nD)\) 的，无法通过。

由于我们要求的是“是否存在一个数 \(x \in (0,X_{q_i - 1}]\) ，使得执行完 \((q_i + 1,n]\) 操作后 \(x\) 变成 \(0\)” ，我们只需要求出最小的那个即可判断，于是改成：

\(dp_i\) 表示最小的 \(x\) ，使得执行完 \([i,n]\) 操作后 \(x\) 不能变成 \(0\)。

转移：

\[dp_i = \begin{cases}dp_{i+1} & dp_{i+1}\le \dfrac{d_i}2 \\ dp_{i+1}+d_i & dp_{i+1} > \dfrac {d_i} 2 \end{cases} \]

时间复杂度 \(O(n)\)。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ARC121D 1 or 2}\)

\(\text{wzxx : “很蠢的，你们是不是降智了?”}\)

单独一组可以看成和 \(0\) 配对，于是可以枚举添加多少个 \(0\)，最优策略一定是头尾配对，取最小值即可。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ARC099F Eating Symbols Hard}\)

用哈希值 \(h_i\) 表示执行完 \(S_{(0,i]}\) 的操作后的序列 \(A\) ：

\[h_i = \sum\limits_{j=-\infty}^{\infty}A_j{Base}^j\pmod {M} \]

对于四个操作：

\[+ \longrightarrow h = h+{Base}^p \]

\[- \longrightarrow h = h - {Base}^p \]

\[> \longrightarrow p = p+1 \]

\[< \longrightarrow p = p-1 \]

记 \(p_i\) 为执行完 \(S_{(0,i]}\) 的操作后 \(P\) 的位置，

考虑只执行 \((l,r]\) 的操作后 \(A\) 的哈希值：

\[h_{(l,r]} = \dfrac {(h_r-h_l)}{{Base}^{p_l}} \]

若合法，则有： \(\dfrac {(h_r-h_l)}{{Base}^{p_l}} = h_n\)

移项得到 \(h_r = h_l + h_n{Base}^{p_l}\)

枚举 \(l\) 数有多少 \(r\) 即可，时间复杂度 \(O(n \log n)\)。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ARC102E Stop. Otherwise...}\)

考虑 \(OGF\) 。

对于 \(ans_i\)，有三种点数：

任意选的，记数量为 \(a\)，\(OGF\) 为 \(\dfrac 1 {1-x}\)；
成对且和为 \(i\) 的数，记数量 \(b\)，\(OGF\) 为 \(\dfrac {1 + x} {1-x}\)；
\(i/2\)，只能取一个，\(OGF\) 为 \(1 + x\)。

则 \(ans_i = \sum\limits_{j=0}^{\infty}[x^j]\dfrac {(1+x)^{b}} {(1-x)^{a+b}}(i\&1 ?1:(1+x))\)

将其简化，变成求 \([x^n]\dfrac {(1+x)^a}{(1-x)^b}\)，推一下：

\[\begin{aligned}[x^n]\dfrac {(1+x)^a}{(1-x)^b}&=[x^n](1+x)^a(1-x)^{-b}\\&=\sum\limits_{i=0}^n[x^i](1+x)^a[x^{n-i}](1-x)^{-b}\\&=\sum\limits_{i=0}^n\dbinom{a}{i}\dbinom{b+(n-i)-1}{n-i}\end{aligned} \]

直接计算，时间复杂度 \(O(nk)\) 。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ AGC013E Placing Squares}\)

先不考虑 \(m\) 个点的限制，记 \(dp_i\) 表示覆盖了前 \(i\) 块的总和，则有：

\[dp_{i+1}=\sum\limits_{j=0}^{i}dp_j(i+1-j)^2 \]

直接做是 \(n^2\) 的。

考虑把 \((i+1-j)^2\) 展开，得到：

\[dp_{i+1}=\sum\limits_{j=0}^idp_j(i-j)^2 + 2\sum\limits_{j=0}^idp_j(i-j)+\sum\limits_{j=0}^idp_j \]

记 \(A_i = \sum\limits_{j=0}^{i-1}dp_j(i-j)^2,B_i = \sum\limits_{j=0}^{i-1}dp_j(i-j),C_i = \sum\limits_{j=0}^{i-1}dp_j\)，则 \(dp_{i+1} = A_{i+1} + B_{i+1} + C_{i+1}\)。

观察到 \(n\) 很大，但是 \(m \le 10^5\)，实际上可以分成 \(O(m)\) 段没有限制的区间，使用前面的 \(dp\) 转移，考虑矩阵快速幂：

假设已经知道 \(\begin{bmatrix}A_i & B_i &C_i\end{bmatrix}\)，求 \(\begin{bmatrix}A_{i+1}&B_{i+1}&C_{i+1}\end{bmatrix}\)。

\(dp_{i} = A_i\)
\(A_{i+1} = A_i + 2B_i + C_i + dp_i = 2A_i + 2B_i + C_i\)
\(B_{i+1} = B_i + C_i + dp_i = A_i + B_i + C_i\)
\(C_{i+1} = C_i + dp_i = A_i + C_i\)

则转移矩阵为：

\[\begin{bmatrix}2&1&1 \\2&1&0\\1&1&1\end{bmatrix} \]

若 \(i\) 点为星星，则转移矩阵为：

\[\begin{bmatrix}1&0&0\\2&1&0\\1&1&1\end{bmatrix} \]

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ARC066E Addition and Subtraction Hard}\)

性质题：

括号只加在减号后面
加了括号后，括号里面的数前面如果有减号，那么一定可以对答案贡献正数

于是直接枚举最外层的左括号，取最大值即可。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ARC060F Best Representation}\)

首先考虑整个串是否有循环节，这个可以使用 \(kmp\) 解决。

若没有循环节，则答案一定为 \(1,1\)；

否则，分类考虑：

循环节是 \(1\)：答案一定为 \(n,1\)；
循环节 \(>1\)：可以发现，\(s_{1..n-1}\) 和 \(s_n\) 可以构成一组合法的解，则最优方案一定是分成两段，于是可以枚举断点数一下有多少合法方案， \(\bmod 1e9+7\) 是唬人的。。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ AGC009C Division into Two}\)

\(\color{black}l\color{red}{bylby}\) ：预测性 dp

记 \(f(i,0/1)\) 表示第 i 个数放入集合 0/1，第 i+1 个数放入集合 1/0 的方案数。

可以得到 \(O(n^2)\) 的暴力，然后发现转移是一段区间，维护一下可以做到 \(O(n)\) 。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ABC213G Connectivity 2}\)

dp 小 trick：钦定某个元素一定出现在某个集合，这样可以不重不漏地计数。

记 cnt(S) 为集合 S 内元素间的总边数， f(S) 为使得集合 S 中的所有点联通的选边方案数，则有：

\[\large f(S) = 2^{cnt(S)} - \sum\limits_{T\subsetneqq S} f(T) 2^{cnt(S/T)} \]

但是这样会算重，可以考虑钦定一个点 u 没有和 S 联通，转移变成：

\[\large f(S) = 2^{cnt(S)} - \sum\limits_{T\subsetneqq S,u\in T}f(T)2^{cnt(S/T)} \]

于是就做完了。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ARC066D Xor Sum}\)

假设已有一对 \(a,b \Longrightarrow u,v\) 合法：

若将 \(a,b\) 各自左移一位，可以得到 \(2a,2b \Longrightarrow 2u, 2v\)。
若左移后 \(a,b\) 其中一方加 \(1\)，得到 \(2a+1,2b \Longrightarrow 2u+1,2v+1\)
若左移后 \(a,b\) 分别都加 \(1\)，得到 \(2a+1,2b+1 \Longrightarrow 2u,2v+2\)

记 \(f(n)\) 为 \(u,v,a,b \le n\) 时的答案，则：

若 \(n\) 为奇数，则 \(f(n) = f(n/2) + f(n/2) + f(n/2-1)=2f(n/2)+f(n/2-1)\)
若 \(n\) 为偶数，则 \(f(n) = f(n/2) + f(n/2-1) + f(n/2-1) = f(n/2) + 2f(n/2-1)\)

时间复杂度 \(O(\log n)\)。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ABC217G Groups}\)

记 \(f_n\) 表示恰好被分成 \(n\) 个不区分的非空集合的方案数，\(g_n\) 表示被分成 \(n\) 个区分集合的方案数。

则有：

\[\large g_n=\sum_{i = 1}^n\dbinom n if_i i!=\prod_{i=0}^{m-1}\dbinom n {cnt_i}cnt_i! \]

二项式反演得到：

\[\large n!f_n = \sum_{i=1}^n(-1)^{n-i}\dbinom n i g_i \]

直接计算即可做到 \(O(n^2)\) 。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ ABC141F Xor Sum 3}\)

可以发现，若二进制下第 \(i\) 位出现了奇数次，无论怎么划分都会答案贡献 \(2^i\)，那么就可以考虑先把出现次数为奇数次的位去掉。

对于出现次数为偶数的位，对答案的贡献要么是 \(2^{i+1}\)，要么是 \(0\)。

假如集合 \(s_1\) 的第 \(i\) 位为 \(1\)，那么 \(s_2\) 的第 \(i\) 位也为一，所以说 \(s_1\) 和 \(s_2\) 只考虑出现次数为偶数的位是相等的，因此用线性基求个最大值即可，时间复杂度 \(O(n \log n)\)。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{「JOISC 2018 Day 3」比太郎的聚会}\)

先建反图，然后考虑根号分治：

\(\odot\) 若 \(y < \sqrt n\)：可以一开始预处理出从每个点出发能到达的 \(k(\le \sqrt n)\) 远点，直接查询即可；

\(\odot\) 若 \(y \ge \sqrt n\)：直接跑最长路，这样的情况最多出现 \(\dfrac q {\sqrt n}\) 次。

总复杂度 \(O(n \sqrt n)\)。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ CF1418G Three Occurrences}\)

这个题可以做到出现恰好 \(k\) 次。（本题 \(k = 3\)）

首先记 \(c(i,j)\) 表示序列前 \(i\) 个数中，\(j\) 出现的次数模 \(k\) 的值。

那么一个合法的区间 \([l,r]\) 满足 \(cnt(l - 1) = cnt(r)\) （整行相同），这个可以哈希做。

但是这样求出来的只满足出现 \(k\) 的倍数次，考虑从前往后扫的时候计算当前右端点能匹配的左端点的最小值 \(lim\)，具体的说：令 \(lim \longleftarrow max(lim, pos(a_i,k+1))\) ，其中 \(pos(a_i,k+1)\) 表示数 \(a_i\) 从 \(i\) 往前数出现的第 \(k + 1\) 次的位置，那么查询的时候只需要确保 \(lim < l\) 即可。

时间复杂度 \(O(n \log n)\) 。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ [JLOI2012]时间流逝}\)

设 \(f_{sum,mn}\) 表示能量和为 \(sum\)，能量最小的能量圈为 \(mn\) 时，使得总和 \(> t\) 的期望步数，记该状态的前驱为 \(pre\)（只有一个），后继为 \(suc\)（可能有多个，为一个集合），则有：

\[f_{sum,mn} = 1 + p * f(pre) + \dfrac {1-p} {|suc|}\sum\limits_{i\in suc}f(i) \]

将前驱记作父亲，后继记作儿子，这个关系就形成了一棵树，\(\color{red}{\text{树上高斯消元}}\) 即可解决这个问题。

主要原理：将每个 \(u\) 写成 \(f(u)=kf(father) + b\) 的形式，从下往上推 \(k,b\) ，根没有父亲，可以直接求出 \(f\) ，由此得到整棵树的 \(f\)。

为了方便，将当前状态记作 \(u\)，先将常数项移到右边，未知项移到左边：

\[f(u)-pf(pre)-\dfrac{1-p}{|suc|}\sum\limits_{i\in suc}f(i)=1 \]

\(\dfrac {1-p} {|suc|}\) 是常数，记作 \(C\)。

由于儿子的形式已经变成了 \(kx+b\) 的形式，记作 \(f(i)=k_if(u)+b_i\)，则：

\[f(u)-pf(pre)-C\sum\limits_{i\in suc}k_if(u)-C\sum\limits_{i\in suc}b_i=1 \]

写成 \(kx+b\) 的形式：

\[f(u)=\dfrac {pf(pre)}{1-C\sum\limits_{i\in suc}k_i}+ \dfrac {C\sum\limits_{i\in suc}b_i + 1}{1-C\sum\limits_{i\in suc}k_i} \]

推到根，\(b\) 就是 \(ans\)。（注：根的 \(c\) 为 \(\dfrac 1 {mn}\)）

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ CF1295F Good Contest}\)

考虑将 \(n\) 个区间划分为若干个不相交的区间，记 \(f_{i,j}\) 表示填完前 \(i\) 个数，第 \(i\) 个数在 \([l_j, r_j)\) 区间内的方案数，直接转移即可，时间复杂度 \(O(n^4)\) 。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ CF878D Magic Breeding}\)

每一位可以单独考虑。

由于每个生物的每个值都来源于起初的 \(k\) 个生物，记 \(f_{i,S}\) 表示第 \(i\) 个生物所有值的来源能否都是 \(S\) 中的生物，\(S\) 代表的是起初的 \(k\) 个生物，这可以表示为 \(ans_i \ge \min\limits_{j \in S} a_j\)。

设添加的生物为 \(cur\)：

对于取 \(\max\) 操作： \(f_{cur,S} = 1\) 满足 \(ans_{x}\ge \min\limits_{j \in S}a_j\) 或 \(ans_y \ge \min\limits_{j \in S} a_j\)，即 \(f_{cur,S} = f_{x,S} | f_{y,S}\)；
对于取 \(\min\) 操作： \(f_{cur,S} = 1\) 满足 \(ans_{x}\ge \min\limits_{j \in S}a_j\) 且 \(ans_y\ge \min\limits_{j \in S} a_j\)，即 \(f_{cur,S} = f_{x,S} \& f_{y,S}\)；
对于询问，将 \(k\) 个生物的第 \(y\) 个值从大到小考虑，若加入第 \(i\) 个生物后使得 \(f_{x,S}\) 的值为 \(1\)，则答案为 \(a_{i,y}\)。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ 三千世界 }\)

考虑转化为求期望，答案乘上 \(2^{n^2}\)。

记 \(f(u,k)\) 表示考虑到点 \(u\)，子树内还有 \(k\) 个点未被覆盖且与 \(u\) 相连（不经过被覆盖的点）的概率。

考虑加入一棵子树 \(f(v,k')\)，有 \(2^{-2kk'}\) 的概率使得 \(k \longrightarrow k+k'\)，剩下的概率使得 \(k \longrightarrow 0\)，树上背包的转移为 \(O(n^2)\) 的，可以通过。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ 「ICPC World Finals 2017」Money for Nothing}\)

\(\color{red}{\texttt{Tag: 决策单调性}}\)

首先可以将问题转化为：

平面内有两种点，求两两之间的矩形面积的最大值

首先排除掉无用的点，使得第一类点 \(x\) 单调递增， \(y\) 单调递减。

考虑以下决策：

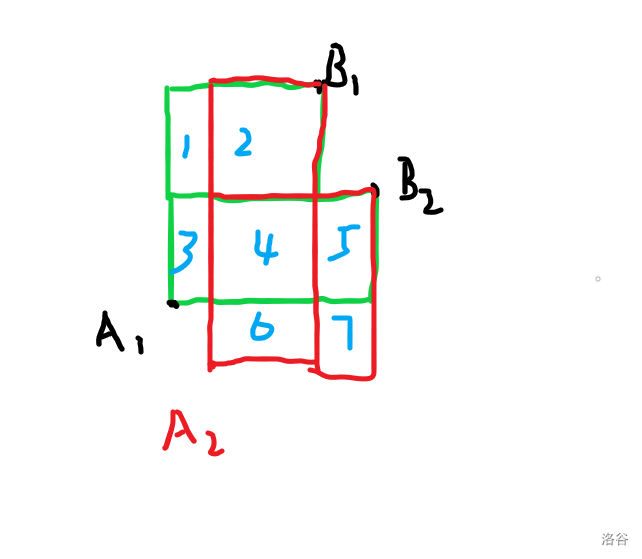
设 \(A_1\) 和 \(B_2\) 匹配优于和 \(B_1\) 匹配，即 \(3+4+5>1+2+3+4\)，整理得 \(5 > 1 + 2\) 。

那么对于 \(A_2\)，与 \(B_1\) 匹配：\(2+4+6\)，与 \(B_2\) 匹配：\(4+6+5+7\)

由于 \(5 > 1 + 2\) ，则 \(5 + 7 > 2\)，即与 \(B_2\) 匹配优于 \(B_1\)。

于是用分治解决决策单调性即可，时间复杂度 \(O(n\log n)\)。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ [NOI2012] 骑行川藏}\)

\(\color{red}{\texttt{Tag: 拉格朗日乘子法}}\)

形式化的：

求 \(f(x_1,x_2,...,x_n)=\sum\limits_{i=1}^n g_i(i)\) 的最值，并且限制 \(\sum\limits_{i=1}^n x_i\) 为 \(lim\)。

记结论：在每个 \(g_i\) 中 \(x_i\) 处的导数都相等时答案最优。

本题中： \(g_i = \dfrac {T_i} {E_i} = \dfrac {s_i / v_i}{k_is_i(v_i-v'_i)^2}\)，满足 \(\sum\limits_{i=1}^nk_is_i(v_i - v'_i)^2=Eu\)。

对于每个 \(T_i\)，其导数为 \(\dfrac {dT} {dE} = \dfrac{-s_iv_i^{-2}}{2k_is_i(v_i-v'_i)}=\dfrac{-1}{2k_iv_i^2(v_i-v'_i)}\)。

由题意可知， \(v_i > v_i'\)，则导数均为负数，并且是单调的。

于是可以二分相等的导数值 \(x\) ，对于每个 \(i\) 二分一个 \(v_i\) 使得其导数为 \(x\)，求出总耗能调整 \(x\)，即可做到 \(O(n \log ^2 n)\) 。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{CF1548C The Three Little Pigs}\)

\(\color{red}{\texttt{Tag: 生成函数}}\)

对于每个 \(x\)，答案为 \(\large\sum\limits_{i = 1} ^ n\dbinom{3i}{x}\) 。

考虑算每个 \(i\) 对答案的贡献，生成函数为 \(\large\sum\limits_{n\ge0}\dbinom {3i} n x^n = (1+x)^{3i}\) ，那么答案的生成函数即为 \(\large\sum\limits_{i=1}^n(1+x)^{3i}\)。

可以发现这是个等比数列，求和得到 \(\large\dfrac{(1+x)^{3n+3} - (1+x)^3}{(1+x)^3 - 1}\)。

分子可以直接算组合数得到每一项的系数，由于分母展开后只有三项，直接暴力多项式除法即可，答案即为多项式的第 \(x\) 项的系数。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ [CEOI2004] Sweets}\)

\(\color{red}{\texttt{Tag: 生成函数}}\)

答案显然为 \(\Large\prod\limits_{i=1}^n\sum\limits_{n=0}^{m_i}x^n = \Large\prod\limits_{i=1}^n \dfrac {1 - x^{m_i + 1}} {1 - x}\) 。

先提出来 \(\Large1-x\) ，得到 \(\Large(1-x)^{-n}\prod\limits_{i=1}^{n}(1-x^{m_i + 1})\)。

对前面使用牛顿二项式定理：

\[\begin{aligned}\Large(1-x)^{-n} &= \Large\sum\limits_{i\ge0}\dfrac{(-n)^{\underline{i}}}{i!}(-x)^i\\ &=\Large\sum\limits_{i\ge0}\dfrac{{(n+i-1)^{\underline{i}}}}{i!}x^i \\ &=\Large\sum\limits_{i\ge0}\dbinom{n+i-1}{i}x^i\end{aligned} \]

由于 \(n\le10\)，后面可以暴力 \(2^n\) 展开，枚举后面得到的每一项，设 \(x^i\) 系数为 \(k_i\)，则对答案的贡献为：

\[\Large k_i\sum\limits_{j=a-k}^{b-k}\dbinom{n + j - 1}{j}=k_i*(\dbinom{n+b-k}{b-k}-\dbinom{n+a-k-1}{a-k-1}) \]

模数是 \(2004\)，不是质数，具体看题解区咋搞。

（“可以先把模数乘上除数，再将运算结果除以除数得到答案”）

\(\texttt{Code}\)

\(\bullet\) \(\texttt{[NOI Online] 游戏}\)

\(\color{red}{\texttt{Tag: dp,二项式反演}}\)

和上题类似 , 记 \(f(i,j)\) 表示以 \(i\) 根的子树中匹配了 \(j\) 个非平局的方案数 , 在树上转移即可。

乍一看是 \(O(n^3)\) 的,实际上这个背包是 \(O(n^2)\) 的。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{已经没有什么好害怕了}\)

\(\color{red}{\texttt{Tag: dp，二项式反演}}\)

组数多 \(k\) 实际上是 \(a > b\) 的组数 \(= \dfrac {n + k} 2\)。

首先将 \(a, b\) 从小到大排序。

记 \(f(i,j)\) 表示 \(a\) 的前 \(i\) 个数中匹配了 \(j\) 个 \(a > b\) 的方案数，则有：

\[f(i,j) = f(i - 1, j) + f(i - 1, j - 1) * (c[i] - (j - 1)) \]

其中 \(c_i\) 表示 \(\sum\limits_{j=1}^n[a_i > b_j]\)。

记 \(g_i\) 为 \(a > b\) 的组数 \(\ge i\) 的方案数，则 \(g_i = (n - i)! f(n, i)\)。

记 \(ans[i]\) 为 \(a > b\) 的组数恰好为 \(i\) 的方案数，则 \(g_i = \sum\limits_{j = i}^n \dbinom j i ans_j\)。

由二项式反演得：\(ans_i = \sum\limits_{j = i}^n(-1)^{j - i}\dbinom j i(n - j)!f(n,j)\)

直接计算 \(ans_{\frac {n + k} 2}\) 即可。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ CF1188D Make Equal}\)

\(\color{red}{\texttt{Tag: 奇妙dp}}\)

假设将最大值 \(mx\) 增大 \(x\)，则最少的操作次数为：

\[\large\sum\limits_{i = 1}^n popcount(mx + x - a_i) \]

首先令 \(a_i = mx - a_i\)，转换成 \(\large\sum\limits_{i = 1}^npopcount(x+a_i)\)。

记 \(f(i,j)\) 为考虑了 \(x\) 的前 \(i\) 位，第 \(i\) 位有 \(j\) 个数进了位的最小操作次数。

假设现在处理到第 \(p\) 位：

可以发现，第 \(p - 1\) 位是否进位的影响很大，若存下每个数上一位是否进位，\(2^n\) 显然是不行的。

~~不难发现，~~ 对 \(2^p\) 取模后最大的数最先进位，因此可以考虑每次都对每个数取模 \(2^p\) 后排序，那么上一位进位的一定是前 \(j\) 大的数，这个问题就解决了。

接下来是转移：(对于第 \(p\) 位)

若 \(x\) 的第 \(p\) 位是 \(1\)：

若 \(a_i\) 的第 \(p - 1\) 位没进位，第 \(p\) 位为 \(1\)，则第 \(p\) 位会进位；

若 \(a_i\) 的第 \(p - 1\) 位没进位，第 \(p\) 位为 \(0\)，则第 \(p\) 为不会进位；

若 \(a_i\) 的第 \(p - 1\) 位进位了，第 \(p\) 位为 \(1\)，则第 \(p\) 位会进位；

若 \(a_i\) 的第 \(p - 1\) 位进位了，第 \(p\) 位为 \(0\)，则第 \(p\) 位也会进位。

若 \(x\) 的第 \(p\) 位是 \(0\)：

若 \(a_i\) 的第 \(p - 1\) 位进位了，且第 \(p\) 位为 \(1\)，则第 \(p\) 位会进位；其余情况均不进位。

实际上我们并不关心 \(a_i\) 是多少，只需要数有多少个数第 \(p\) 位为 \(1\) 就行。

\(\texttt{Code}\)

\(\bullet\) \(\texttt{ [HNOI2015]亚瑟王}\)

\(\color{red}{\texttt{Tag: 奇妙dp，概率期望}}\)

考虑计算每张牌的期望伤害值，答案即为总和。

一个巧妙的 \(dp\) ：记 \(f(i,j)\) 为前 \(i\) 张牌中，已经触发了 \(j\) 张牌的概率。

则有：

若第 \(i\) 张牌最终没有打出，则剩余的 \(r - j\) 轮必须都没打出，即 \(f(i,j)\) 加上 \(f(i-1,j) * (1-p[i])^{r-j}\)。
若第 \(i\) 张牌最终打出去了，则 \(r - j + 1\) 轮必须有一轮成功打出，即 \(f(i,j)\) 加上 \(f(i - 1, j - 1) * (1 - (1 - p[i]) ^ {r - j + 1})\)。