P12992 [GCJ 2022 #1C] Intranets 题解

题目传送门

感觉是一道很酷的推式子题耶（

我们考虑类似联通块等于点减边的形式，按大小从大到小跑，如果一条边两边至少有一个点没被标记，那么标记两边，边数加一。

联通块个数就为 \(n\) 减去那些边，就相当于强行对于基环树把最小的边删去不看，考虑每次都是标记 \(1\) 到 \(2\) 个点，那么每标记两个点的边出现一次，联通块个数就多一个。

所以本质上联通块个数为一条边同时是两边最大值的边的个数，我们称这种边为关键边。

如果有一定计数基础有第一步后做起来就会很舒服。

考虑容斥，算 \(\ge i\) 的关键边的，枚举 \(i \ge k\)，乘系数 $-1^{i-k}\times \binom{i}{k} $。

然后考虑选 \(i\) 条边出来，并且钦定一个顺序，就是 \(\binom{m}{2i} \times (2i-1)!!\times i!\)，双阶乘的定义是 \(i \times (i-2) \times (i-4)...\)。

还有一些边是有限制的，如果该边与其它关键边相连，选择编号最小的边相连即可（编号就是我们钦定的顺序）。

对于编号最小的点，有 \(2n-4\) 条边都必须比它小，然后第二小的就有 \(2n-8\) 条边（有四条是和前面的），以此类推，所以第 \(i\) 个点的子树大小为 \(i+\sum_{j=1}^{i}\left(2n-4j\right)\)，然后其它都是叶子子树大小都是 \(1\)。

\(n\) 个点的树的拓扑序个数是怎么搞的捏，考虑一颗内向树，\(1\) 为根，对于每个点，它是子树内最小的，然后给子树随意分配一些点，也就是 \(f_i = \frac{(siz_i-1)!}{siz_{u_1}!siz_{u_2}!}\times f_{u_1}\times f_{u_2}...\)。考虑把这些乘起来，其实就是 \(\frac{1}{siz_2\times siz_3\times...}\)，第一个点大小为 \(n\)，所以其实就是 \(\frac{n}{siz_1\times siz_2\times...}\)。

我们已经知道了每一个的子树大小，直接带进去，具体式子如下，我实在是不想写了/kel

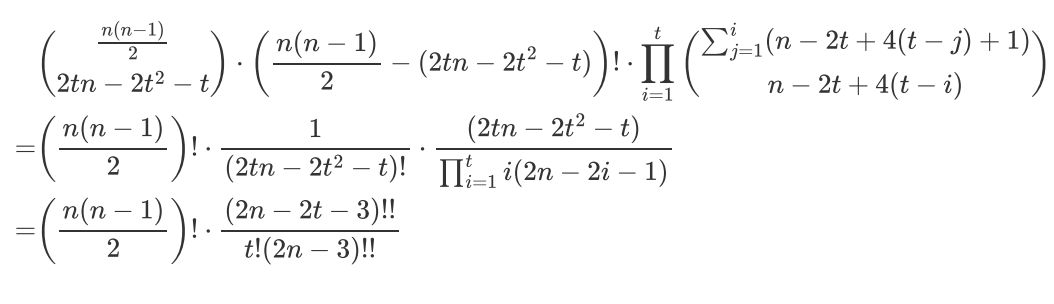
第一个东西就和概率约掉了，不需要算了。

全部带入答案就是 \(\sum_{i=k}^{i \le \left \lfloor \frac{m}{2} \right \rfloor }-1^{i-k}\times \binom{i}{k} \times \binom{m}{2i} \times (2i-1)!! \frac{(2n-2i-3)!!}{(2n-3)!!}\)。

好像还可以推，具体参见讨论区和洛谷第一篇题解。

code

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define getchar() (p1 == p2 && (p2 = (p1 = buf1) + fread(buf1, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
char buf1[1 << 23], *p1 = buf1, *p2 = buf1, ubuf[1 << 23], *u = ubuf;
namespace IO
{
	template<typename T>
	void read(T &_x){_x=0;int _f=1;char ch=getchar();while(!isdigit(ch)) _f=(ch=='-'?-1:_f),ch=getchar();while(isdigit(ch)) _x=_x*10+(ch^48),ch=getchar();_x*=_f;}
	template<typename T,typename... Args>
	void read(T &_x,Args&...others){Read(_x);Read(others...);}
	const int BUF=20000000;char buf[BUF],to,stk[32];int plen;
	#define pc(x) buf[plen++]=x
	#define flush(); fwrite(buf,1,plen,stdout),plen=0;
	template<typename T>inline void print(T x){if(!x){pc(48);return;}if(x<0) x=-x,pc('-');for(;x;x/=10) stk[++to]=48+x%10;while(to) pc(stk[to--]);}
}
using namespace IO;
const int N = 2e7+10,M = 2e7,mod = 1e9+7;
int t,m,k,ans,fac[N],Fac[N],inv[N],Inv[N],x,y,z;
inline int ksm(int x,int p)
{
	int ans = 1;
	while(p)
	{
		if((p&1)) ans = ans*x%mod;
		x = x*x%mod,p >>= 1;
	}
	return ans;
}
inline int C(int x,int y){ return fac[x]*inv[y]%mod*inv[x-y]%mod; }
signed main()
{//9673679 1595677 998244353

//	freopen(".in","r",stdin);
//	freopen(".out","w",stdout);
	read(t);
	 fac[0] = fac[1] = Fac[0] = Fac[1] = 1;
	for(int i = 2;i <= M;i++) Fac[i] = Fac[i-2]*i%mod,fac[i] = fac[i-1]*i%mod;
	inv[M] = ksm(fac[M],mod-2);
	for(int i = M-1;i >= 0;i--) inv[i] = inv[i+1]*(i+1)%mod;
	Inv[M] = ksm(Fac[M],mod-2);
	Inv[M-1] = ksm(Fac[M-1],mod-2);
	for(int i = M-2;i >= 0;i--) Inv[i] = Inv[i+2]*(i+2)%mod;
	for(int j = 1;j <= t;j++)
	{
		printf("Case #%lld: ",j);
		read(m),read(k);
		ans = 0; x = 1;
		for(int i = k;i <= m/2;i++) 
		{
			if(2*m-3-2*i >= 0) ans = (ans+x*C(i,k)*C(m,2*i)%mod*Fac[2*i-1]%mod*Inv[2*m-3]%mod*Fac[2*m-3-2*i]%mod+mod)%mod,x *= -1;
			else ans = (ans+x*C(i,k)*C(m,2*i)%mod*Fac[2*i-1]%mod*Inv[2*m-3]%mod+mod)%mod,x *= -1;
		//	cout<<ans<<" "<<C(i,k)<<" "<<C(m,2*i)<<'\n';
		}
		//C(n,2*i)*(2*i-1)!!*i!
		print(ans),pc('\n');
		flush();
	}
	flush();
	return 0;
}
/*
考虑无向变有向
环最大为2，也就是联通块个数
容斥，枚举>=i的联通块方案数
 
(j<=i)2*n-4j = -2i^2+2ni-i = 2ni-2j(j+1)
2n-1-2i
 
n 个点的树的拓扑序个数 是n!*(1/siz_i)
每个点，它是最大，所以是f_i = (siz_i-1)!*(1/siz_u!)*f_u u是i儿子
每个都是这样，考虑下面是siz_i!（没有siz_1的）
上面是(siz_i-1)!的阶乘
上面多一个siz_1!就好了，然后就是上式 
*/