2394: 洗盘子 题解

题目传送门： 2394: 洗盘子

下面把这道「两人分工洗盘子/擦盘子」的栈模拟题完整讲清楚，并给出带详细注释的可交互/可通过版本代码。

---

思路解析（为什么用栈，顺序为何会变化）

• 有三摞盘子：
  dirty（未洗）、wash（洗好待擦）、clean（已擦干）。
  三者都是**后进先出（LIFO）**的典型结构，所以用 stack<int> 最合适。

• 初始状态：1 在顶、N 在底，所以初始化时让 1 在 dirty 栈顶。实现方式是先把 N…1 依次压栈（最后压 1，1 就在顶）。

• 两种操作：

  1. op=1（洗盘子）：从 dirty 顶连拿 k 个，按顺序压入 wash。
     这一步会反转这 k 个盘子的相对顺序（因为从 dirty 顶依次弹出，wash 顶先得到最后一个）。
  2. op=2（擦盘子）：从 wash 顶连拿 k 个，按顺序压入 clean。
     这一步又对这 k 个盘子的相对顺序再反转一次。

• 虽然“洗一次反转、擦一次又反转”看上去像“复原”，但由于洗/擦是分段交替进行的，不同分段之间会“打散”顺序，因此整体顺序并非简单的 1..N，而是取决于每次洗/擦的批量大小和时机。

• 直到 clean 中达到 N 个为止，就完成了全部操作。输出顺序要求“从顶到底”，也就是把 clean 栈从顶依次弹出打印。

---

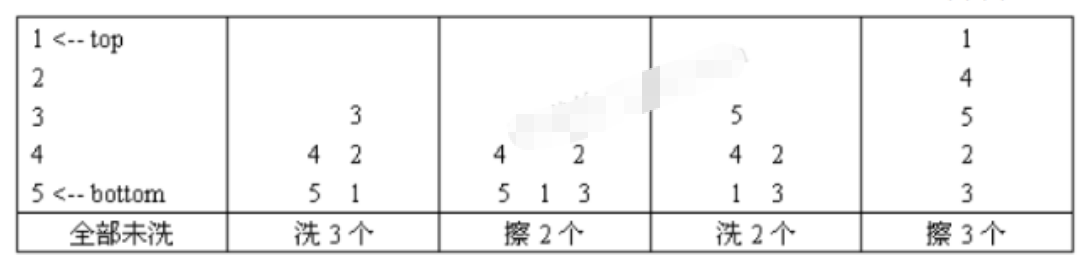
样例推演（题面示例）

N=5；操作：
1 3（洗 3 个）：dirty 顶 1,2,3 进 wash → wash 顶序：[3,2,1]
2 2（擦 2 个）：从 wash 顶取 3、2 进 clean → clean 顶序：[2,3] （顶在左）
1 2（洗 2 个）：把 4、5 压到 wash 顶 → wash 顶序：[5,4,1]
2 3（擦 3 个）：从 wash 顶取 5、4、1 进 clean
最终 clean 从顶到底是：1, 4, 5, 2, 3 —— 与样例一致。

---

复杂度

每个盘子最多被移动两次（进 wash、进 clean），总操作为 O(N)，空间 O(N)。N ≤ 10^4，完全没问题。

---

代码（含健壮性处理 + 详细注释）

#include <bits/stdc++.h>
using namespace std;

/*
  问题：三栈模拟
    - dirty：未洗；初始 1 在顶、N 在底
    - wash ：洗好待擦
    - clean：已擦干；最终从顶到底输出
  操作：
    op=1, k：从 dirty 顶拿 k 个压入 wash
    op=2, k：从 wash  顶拿 k 个压入 clean
  终止条件：clean 中累计达到 N 个
*/

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int N;
    if (!(cin >> N)) return 0;

    stack<int> dirty, wash, clean;

    // 初始化：将 N..1 依次压入，使 1 在栈顶、N 在栈底
    for (int i = N; i >= 1; --i) dirty.push(i);

    long long dried = 0;  // 已擦干的盘子数量
    int op, k;

    // 读取操作直到 clean 数量达到 N
    // 题目保证给出的操作合法且足够完成任务
    while (dried < N && (cin >> op >> k)) {
        if (op == 1) {
            // 洗盘子：从 dirty 顶取 k 个到 wash
            //（若严格防御，可检查 dirty.size() >= k）
            for (int i = 0; i < k; ++i) {
                int x = dirty.top();
                dirty.pop();
                wash.push(x);
            }
        } else if (op == 2) {
            // 擦盘子：从 wash 顶取 k 个到 clean
            //（若严格防御，可检查 wash.size() >= k）
            for (int i = 0; i < k; ++i) {
                int x = wash.top();
                wash.pop();
                clean.push(x);
                ++dried;
            }
        } else {
            // 非法操作码（按题意不会出现），这里忽略或直接结束
            // break;
        }
    }

    // 输出 clean 从顶到底的顺序：逐个弹出打印
    while (!clean.empty()) {
        cout << clean.top() << "\n";
        clean.pop();
    }

    return 0;
}

---

易错点与小贴士

1. 初始化方向：一定要确保 1 在 dirty 的栈顶。常见错误是直接从 1..N 压栈，导致 N 在顶。正确方式是从 N 递减到 1 依次压栈。
2. 读入循环条件：以“已擦干数量 == N”为终止条件最稳妥；不建议用 while (!cin.eof())。
3. 边界检查：题面默认输入合法；若要更稳，可在操作前判断 k 是否超过可用数量。
4. 输出方向：题目要求“从顶到底”，所以直接弹 clean.top() 输出即可。