算法学习笔记: 树的重心
计算以无根树每个点为根节点时的最大子树大小,这个值最小的点称为无根树的重心。本文将证明树的重心的一些数学性质,并给出寻找重心的方法。
在后文中,我将用 (maximum subtree size)表示最大子树大小。用 表示以 为根节点时包含 的子树的大小,用 和 这样的记法表示边和简单路径。此外,我们设整棵树大小为 。
我们首先证明一些简单的引理。例如,设 、 相邻,则 。因为树上任意节点 要么在以 为根 所在的子树上,此时 或存在 ;要么在以 为根 所在的子树上,此时 或存在 。
还有,设存在 ,则 。这是因为 ,故 。实际上,设 ,根据不等式的传递性, 也成立。
无根树的重心主要有以下性质:
性质1
某个点是树的重心等价于它最大子树大小不大于整棵树大小的一半。
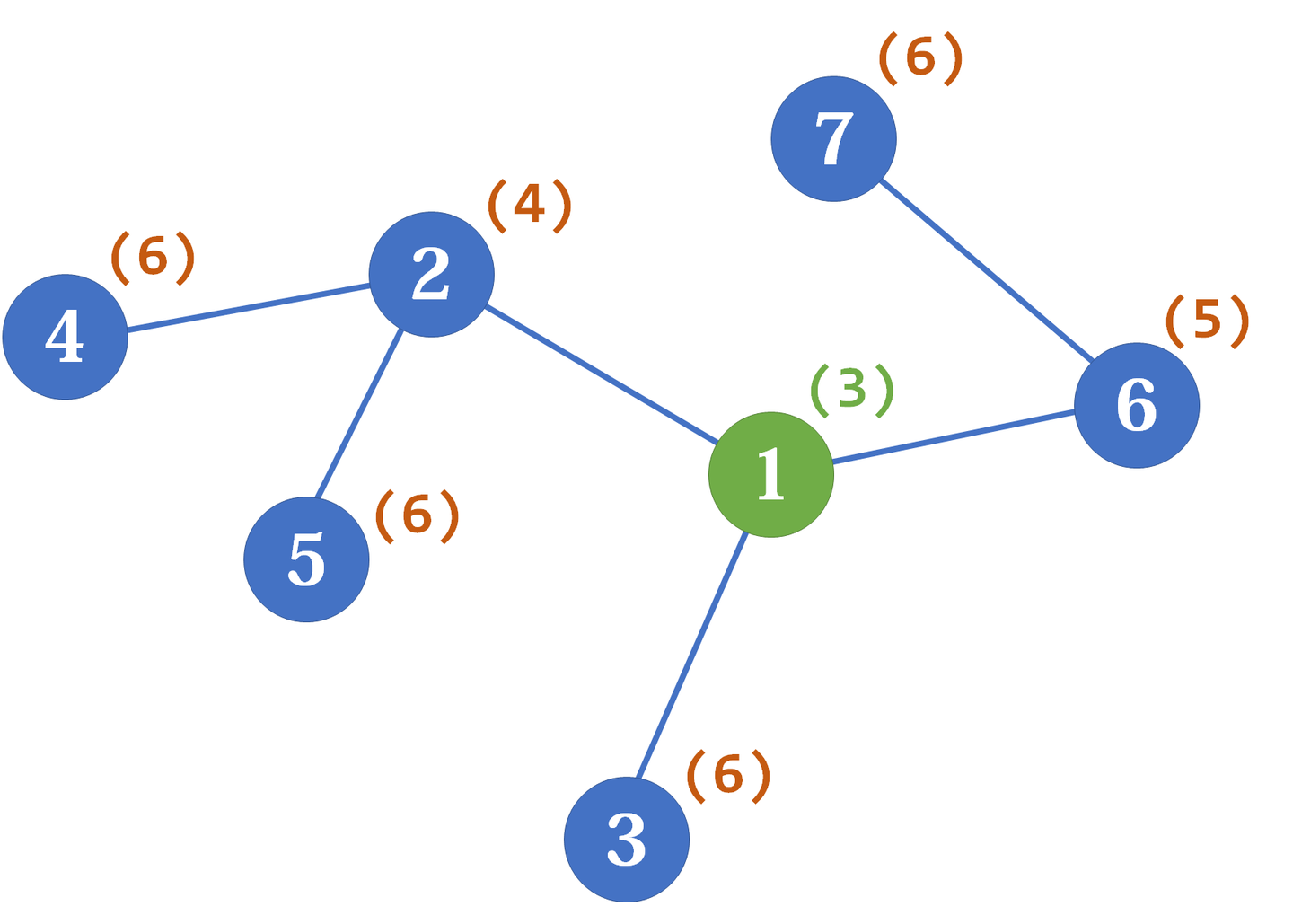
充分性:假设 是树的重心, 与它相邻且 。那么以 为根节点时, ,同时对于 又有 。所以, ,与 是重心矛盾。因此原命题成立。
必要性:假设 是树的重心,且任意与它相邻的节点 都满足 ,那么 ,故 ,则 。对于任意不与 相邻的节点 ,都存在简单路径 ,那么 ,因此 。综上, 是所有节点中 最小的(或之一),也就是树的重心。
性质2
树至多有两个重心。如果树有两个重心,那么它们相邻。此时树一定有偶数个节点,且可以被划分为两个大小相等的分支,每个分支各自包含一个重心。
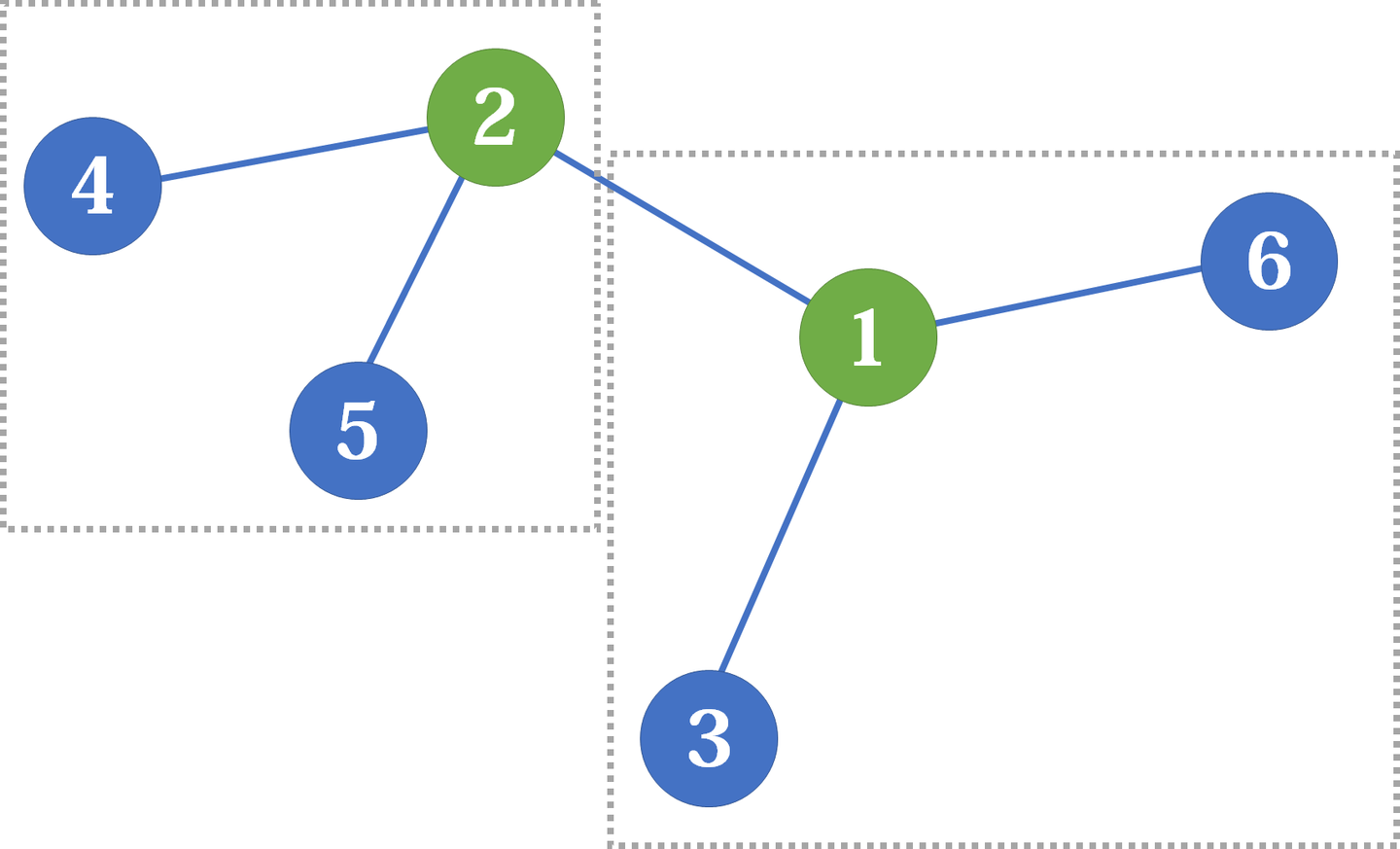
假设 和 是树的两个重心,且它们之间的路径(不包含端点)有 个节点。我们知道 且 ,所以 。
那么 的最大子树必然包含 ,否则设 是 最大子树上任意一点, 有 ,与前面的结论矛盾。同理, 的最大子树也一定包含 。
设 除端点外包含 个顶点,那么 ,可知 。因此,重心必然相邻。
假设树至少存在三个重心,那么它们两两相邻,但这会形成环,是不可能的。所以树最多有两个重心。
由上述条件,我们知道 。而我们又有 ,于是 。所以,在有两个重心时,树的大小一定是偶数,且可以被划分为两个大小相等的分支,每个分支各自包含一个重心。
性质3
树中所有点到某个点的距离和中,到重心的距离和是最小的;如果有两个重心,那么到它们的距离和一样。反过来,距离和最小的点一定是重心。
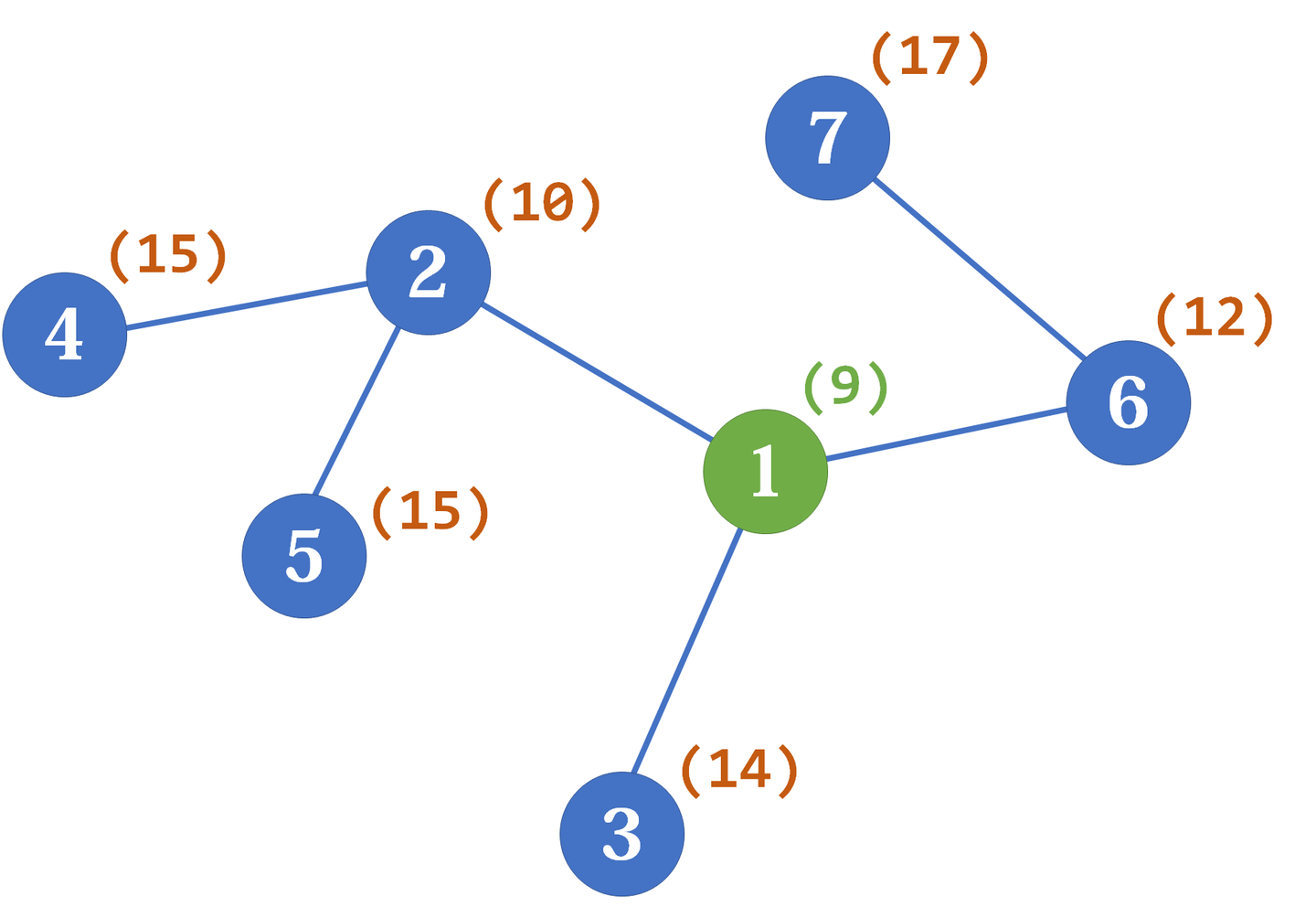
设所有点到某个点 的距离和为 。那么对于树上任意一个点 ,如果存在相邻的点 使得 ,则 ,因为这种移动使得 所在的子树上的点对 的贡献减1,而其他点对 的贡献加1,所以 比 少了 。
除了重心以外的点都至少存在一个相邻点使得 更小,根据偏序关系的性质,重心应当比其他点的 都小。
假设有两个重心 和 。当我们从 移动到 时, 所在分支对 的贡献加了1, 所在分支对 的贡献减了1。由于 所在分支的大小为 , 所在分支的大小为 ,而我们已经知道 ,所以这两个贡献变化刚好互相抵消了。这就导出了 。
上面已经说明了如果一个点不是重心,它相邻的某个点的 一定比它小,所以不是距离和最小的点。因此,距离和最小的点就是重心。
性质4
往树上增加或减少一个叶子,如果原节点数是奇数,那么重心可能增加一个,原重心仍是重心;如果原节点数是偶数,重心可能减少一个,另一个重心仍是重心。[1]
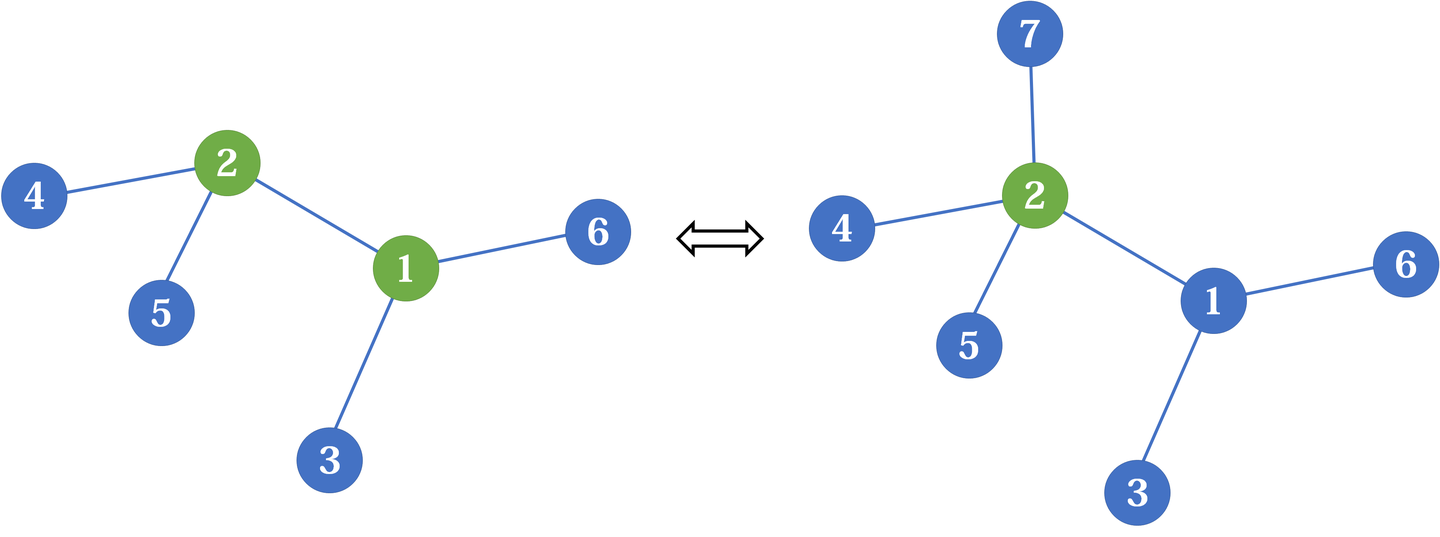
重心的每棵子树的节点数都是小于等于 的,很显然,节点数等于 的子树最多只有一棵。这时 显然是偶数,而且这棵子树的根节点也必然是重心,它也拥有一棵节点数等于 的子树。
增加一个叶子,节点数变成 。如果此时原来的某个重心不再是重心,那么添加叶子的那棵子树原来的节点数一定大于 ,只有节点数等于 的子树才符合要求,这时 只能是偶数。往这棵子树上添加一个节点后,这棵子树的根节点(“另一个重心”)仍然是重心,它拥有一个节点数为 的子树和另外一系列节点数总和为 的子树,均小于 。
如果增加叶子后出现了新的重心,那么添加叶子的那颗子树原来的节点数大于 ,却又小于等于 ,那就只能是 ,这时 一定是奇数。这时原来的重心拥有一棵大小为 的子树和一系列节点数总和为 的子树,仍然是重心。
删除的情形可以类似地证明,不赘述了。
性质5
把两棵树通过一条边相连得到一棵新的树,则新的重心在较大的一棵树一侧的连接点与原重心之间的简单路径上。如果两棵树大小一样,则重心就是两个连接点。[2]
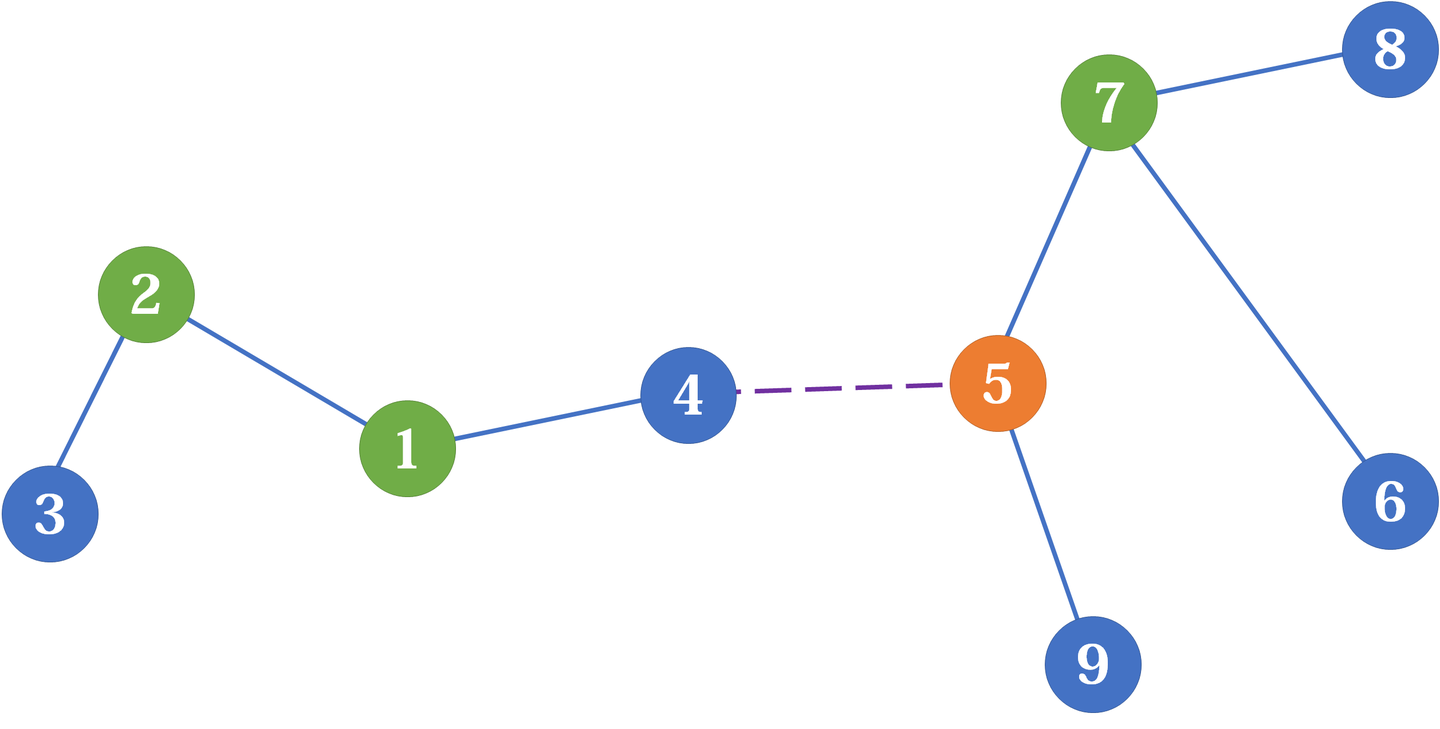
两棵树大小一样的情形显然。
设两棵树的节点数分别为 和 ( ),我们先建出较大的树,然后一个点一个点地把较小的树添加进来。按照性质4,这个过程中可能会出现重心的增加和减少,我们把一组增加和减少称为移动,则重心一定是往连接点方向移动的。
现在只需要证明重心不可能逾越自己一侧的连接点。事实上,当重心达到自己一侧的连接点时,设这时已经添加了 个节点,那么想要通过再添加一个节点让另一侧的连接点也成为重心,需要满足 ,即 。然而 (注意 不能等于 ,因为还要再添加一个节点),所以这是不可能的。
找重心
利用性质1,一趟dfs即可。
int n, sz[MAXN], mss[MAXN]; // n:总结点数(请从外部传入),sz:树的大小,mss:最大子树大小
vector<int> ctr; // 重心
void dfs(int p, int fa = 0) // 找重心
{
sz[p] = 1, mss[p] = 0;
for (auto [to, w] : edges[p])
if (to != fa)
{
dfs(to, p);
mss[p] = max(mss[p], sz[to]);
sz[p] += sz[to];
}
mss[p] = max(mss[p], n - sz[p]);
if (mss[p] <= n / 2) ctr.push_back(p);
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号