两角和差的正余弦公式的若干证明方法

1. 几何方法

1.1. 矩形

1.2. 面积法

1.3. 正弦定理

1.4. 托勒密定理

1.5. 弦图

1.5.1. 外弦图

1.5.2. 内弦图

2. 坐标方法

2.1. 距离公式+余弦定理

2.2. 距离公式+全等

3. 向量方法

4. 复数方法

两角和差的正余弦公式，是整个三角恒等变形的基础，其它的恒等变形的公式，都是由这几个公式推导得到。因此，如何证明第一个公式，是一个很重要的问题。

这里我们整理几种常见证明方法。

1. 几何方法

几何方法的好处是与初中锐角三角函数的内容联系紧密，但是缺点只对锐角（甚至是两角和为锐角）的情况成立，而且不好推广。

1.1. 矩形

如图1，

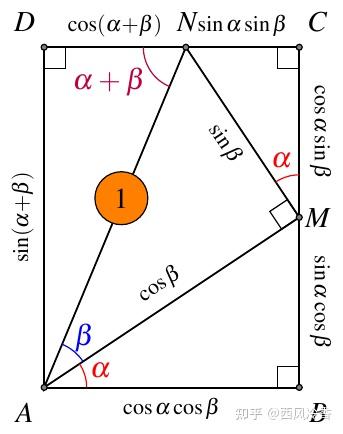
由矩形的对边相等可得

$\begin{aligned} \sin (α + β) & = \sin α \cos β + \cos α \sin β \\ \cos (α + β) & = \cos α \cos β - \sin α \sin β \end{aligned}$

1.2. 面积法

在 $△ A B C$ 中， $A D ⊥ B C$ 于 $D$ ， $∠ B A D = α$ ， $∠ C A D = β$ ，如图2，

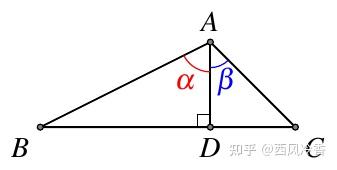
有

$S_{△ A B C} = S_{△ A B D} + S_{△ A C D}$

即

$\frac{1}{2} A B \cdot A C \sin (α + β) = \frac{1}{2} A B \cdot A D \sin α + \frac{1}{2} A C \cdot A D \sin β$

于是

$\begin{aligned} \sin (α + β) & = \frac{A D}{A C} \cdot \sin α + \frac{A D}{A B} \cdot \sin β \\ = \cos β \sin α + \cos α \sin β \end{aligned}$

另外，也可以直接由张角定理得到同样的形式。

1.3. 正弦定理

在上面的图2中，根据正弦定理，有

$\frac{\sin ∠ B A C}{B C} = \frac{\sin B}{A C} = \frac{\sin C}{A B}$

即

$\begin{aligned} \frac{\sin (α + β)}{B C} & = \frac{\sin (90^{\circ} - α)}{A C} = \frac{\sin (90^{\circ} - β)}{A B} \\ = \frac{\cos α}{A C} = \frac{\cos β}{A B} \end{aligned}$

注意

$B C = B D + D C = A B \sin α + A C \sin β$

又有

$\frac{\sin (α + β)}{B C} = \frac{\cos β \sin α + \cos α \sin β}{A B \sin α + A C \sin β}$

于是有

$\sin (α + β) = \cos β \sin α + \cos α \sin β$

1.4. 托勒密定理

在半径为 $R$ 的圆的一个内接四边形 $A B C D$ 中， $∠ A B C = ∠ A D C = 90^{\circ}$ ，如图3，

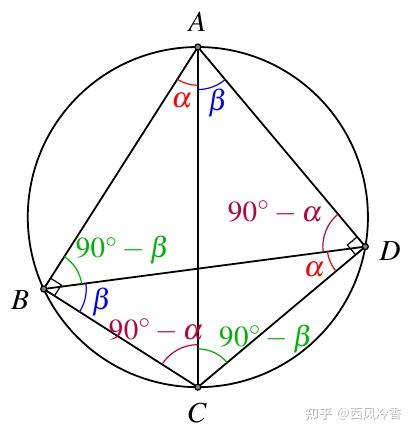
根据托勒密定理，有

$A B \cdot C D + A D \cdot B C = A C \cdot B D$

结合正弦定理可得

$2 R \sin (90^{\circ} - α) \cdot 2 R \sin β + 2 R \sin (90^{\circ} - β) \cdot 2 R \sin α = 2 R \sin 90^{\circ} \cdot 2 R \sin (α + β)$

化简得

$\cos α \sin β + \cos β \sin α = \sin (α + β)$

1.5. 弦图

我们可以用弦图来证明勾股定理。在原始的弦图中，四个小三角形是全等的。我们可以对它做一下变形，把四个全等的三角形改成两组全等的三角形，这样形成的弦图就不是两个正方形了，而是矩形和菱形。

1.5.1. 外弦图

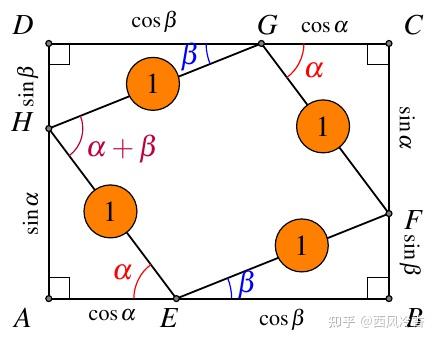
如图4，计算面积可得

$\begin{aligned} 2 \cdot \frac{1}{2} \sin α \cdot \cos α + 2 \cdot \frac{1}{2} \sin β \cdot \cos β + 1 \cdot 1 \cdot \sin (α + β) \\ = & (\sin α + \sin β) (\cos α + \cos β) \end{aligned}$

化简即可得到两角和的正弦公式。

1.5.2. 内弦图

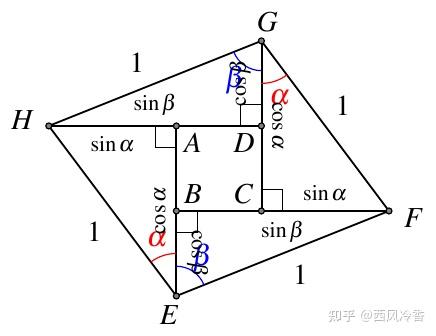
如图5，计算面积可得

$\begin{aligned} 2 \cdot \frac{1}{2} \sin α \cdot \cos α + 2 \cdot \frac{1}{2} \sin β \cdot \cos β + (\sin β - \sin α) (\cos α - \cos β) \\ = & 1 \cdot 1 \cdot \sin (α + β) \end{aligned}$

化简即可得到两角和的正弦公式。

2. 坐标方法

2.1. 距离公式+余弦定理

如图6，在平面直角坐标系 $x O y$ 中，角 $α$ 和角 $β$ 的终边分别与单位圆交于点 $A (\cos α, \sin α)$ 、 $B (\cos β, \sin β)$ ，则 $∠ A O B = α - β$ ，

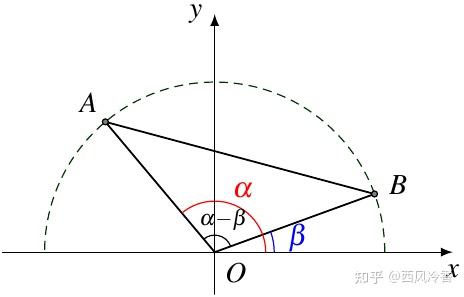
根据距离公式，

$\begin{aligned} | A B |^{2} & = {(\cos α - \cos β)}^{2} + {(\sin α - \sin β)}^{2} \\ = 2 - 2 (\cos α \cos β + \sin α \sin β) \end{aligned}$

根据余弦定理，

$\begin{aligned} | A B |^{2} & = | O A |^{2} + | O B |^{2} - 2 | O A | \cdot | O B | \cos (α - β) \\ = 2 - 2 \cos (α - β) \end{aligned}$

于是有

$\cos (α - β) = \cos α \cos β + \sin α \sin β$

2.2. 距离公式+全等

如图7，我们把上图中的 $△ O B A$ 旋转到 $△ O M P$ ，则 $△ O B A ≅ △ O M P$ ，

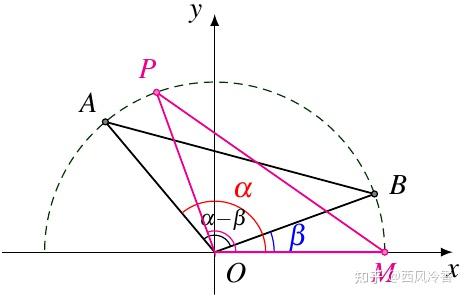
因此 $∠ M O P = ∠ B O A = α - β$ ， $P$ 点的坐标为 $(\cos (α - β), \sin (α - β))$ ，所以

$\begin{aligned} | A B |^{2} = | P M |^{2} & = {(\cos (α - β) - 1)}^{2} + \sin^{2} (α - β) \\ = 2 - 2 \cos (α - β) \end{aligned}$

得到了上一种方法同样的式子。

这种方法对比上一种方法的好处是避开了余弦定理。

3. 向量方法

在平面直角坐标系 $x O y$ 中，角 $α$ 和角 $β$ 的终边分别与单位圆交于点 $A (\cos α, \sin α)$ 、 $B (\cos β, \sin β)$ ，则 $∠ A O B$ 等于 $β - α$ 或 $α - β$ ，或者和其中一个相差 $2 k π$ 。因此

$\begin{aligned} \cos (α - β) & = \cos ∠ A O B = \frac{\vec{O A} \cdot \vec{O B}}{| \vec{O A} | \cdot | \vec{O B} |} = \vec{O A} \cdot \vec{O B} \\ = (\cos α, \sin α) \cdot (\cos β, \sin β) = \cos α \cos β + \sin α \sin β \end{aligned}$

我们看到，向量法的好处是不需要讨论 $α$ 和 $β$ 的情况，而且证明的过程非常简洁。

4. 复数方法

利用复数的指数形式和欧拉公式也可以很容易推出和角公式：

$\begin{aligned} \cos (α + β) + i \sin (α + β) \\ = & e^{i (α + β)} \\ = & e^{i α} e^{i β} \\ = & (\cos α + i \sin α) (\cos β + i \sin β) \\ = & (\cos α \cos β - \sin α \sin β) + i (\sin α \cos β + \cos α \sin β) \end{aligned}$

对比两边的实部和虚部就可以得到两角和的正弦和余弦公式。

参考资料：

两角和与差的余弦公式的五种推导方法之对比
HPM视角下的两角和与差的余弦公式教学，数学教学2019年第3期
Wikipedia: List of trigonometric identities
MathWorld: Trigonometric Addition Formulas

posted @ 2025-05-13 21:40 kkman2000 阅读(317) 评论(0) 收藏举报

刷新页面返回顶部

kkman2000

两角和差的正余弦公式的若干证明方法

两角和差的正余弦公式的若干证明方法

1. 几何方法

1.1. 矩形

1.2. 面积法

1.3. 正弦定理

1.4. 托勒密定理

1.5. 弦图

1.5.1. 外弦图

1.5.2. 内弦图

2. 坐标方法

2.1. 距离公式+余弦定理

2.2. 距离公式+全等

3. 向量方法

4. 复数方法

公告