【基础算法】二分查找
一、算法原理
二分查找适用于在有序数组中查找一个元素,使用了分治思想。
每次比较要查找的元素与数组的中间元素,如果要查找的元素 > 中间元素,在数组后半部分继续查找;如果要查找的元素 < 中间元素,在数组前半部分继续查找;如果要查找的元素 = 中间元素,查找结束。
二分查找通过比较要查找的元素与数组的中间元素,每次将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为 0。
示例:在有序数组 arr = [8,11,19,23,27,33,45,55,67] 中查找数字 33 的位置。
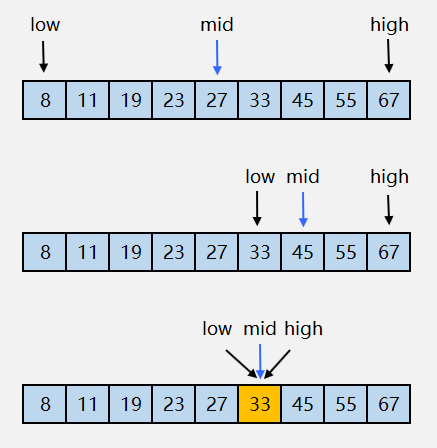
二分查找如果没找到目标数字,那么最后 mid 指向的位置,就是保持数组有序,目标数字插入数组应该在的位置。
示例:在有序数组 arr = [8,11,19,23,27,33,45,55,67] 中查找数字 32 的位置。
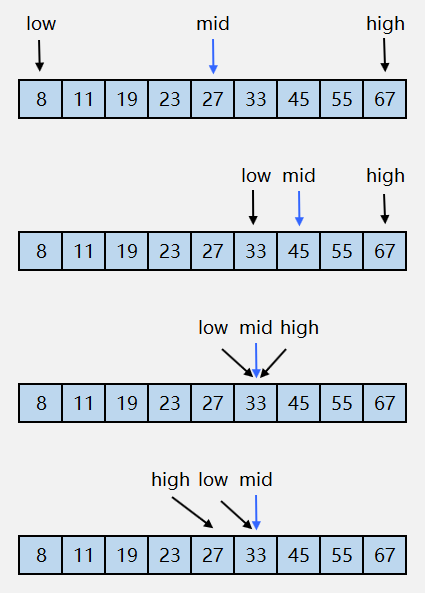
二、代码实现
2.1 循环实现
/**
* 二分查找,时间复杂度:O(logn),空间复杂度:O(1)
*
* @param arr 有序数组
* @param target 要查找的目标数字
* @return 数组包含目标数字,返回目标数字的位置;数组不包含目标数字,返回目标数字应该插入数组的位置
*/
public static int binarySearch(int[] arr, int target) {
int low = 0;
int high = arr.length - 1;
int mid = -1;
while (low <= high) {
mid = (low + high) >> 1;
if (target < arr[mid]) { // 目标数字 < 数组中间数字,在左半部分查找
high = mid - 1;
} else if (target > arr[mid]) { // 目标数字 > 数组中间数字,在右半部分查找
low = mid + 1;
} else { // 目标数字 = 数组中间数字,找到
return mid;
}
}
return mid;
}注意点:
1. 循环退出条件
low <= high,不是 low < high。
2. low 和 high 的更新
low = mid + 1,high = mid - 1,如果写成 low = mid,high = mid,会出现死循环。比如 low = 2,high = 2,如果 arr[2] != target,会死循环。
2.2 递归实现
/**
* 二分查找,递归实现
*
* @param arr 有序数组
* @param low 待查找的区间左边界
* @param high 待查找的区间右边界
* @param target 要查找的目标数字
* @return 数组包含目标数字,返回目标数字的位置;数组不包含目标数字,返回 -1
*/
public static int binarySearch(int[] arr, int low, int high, int target) {
if (low > high) {
return -1;
}
int mid = (low + high) >> 1;
if (target < arr[mid]) {
return binarySearch(arr, low, mid - 1, target);
} else if (target > arr[mid]) {
return binarySearch(arr, mid + 1, high, target);
} else {
return mid;
}
}
三、二分查找的速度惊人
二分查找是一种非常高效的查找算法,其最坏时间复杂度为 O(log2n)。分析过程如下:
假设数据大小是 n,每次查找后数据都会缩小为原来的一半,也就是会除以 2。最坏情况下,直到查找区间被缩小为空,才停止。被查找区间的大小变化情况是 n, n/2, n/4, n/8...n/2k,当 n/2k = 1 时,k 的值就是区间缩小的次数,每次区间缩小只涉及两个数字的大小比较,所以,经过 k 次区间缩小,时间复杂度就是 O(k)。由 n/2k = 1 可知,k = log2n,所以,二分查找的最坏时间复杂度为 O(log2n)。
O(log2n) 的时间复杂度是非常恐怖的,即使 n 特别大,log2n 也很小,比如 n = 232,约等于 42 亿,log2n = 32。也就是说,在 42 亿个数字中使用二分查找,最多只需要比较 32 次。
四、应用场景及局限性
二分查找虽然非常高效,但是也有很大的局限性,主要表现在以下四方面:
4.1 依赖数组随机访问的特点
二分查找需要按照下标随机访问元素,数组按照下标随机访问元素的时间复杂度是 O(1),而链表随机访问的时间复杂度是 O(n)。所以,如果数据使用链表存储,二分查找的时间复杂就会变得很高。
4.2 针对的是有序数组
二分查找数据必须是有序的。如果数据无序,需要先排序。我们知道,排序的时间复杂度最低是 O(nlogn)。所以,如果是一组静态数据,没有频繁地插入、删除操作,我们可以进行一次排序,多次二分查找。这样排序的成本可被均摊,二分查找的边际成本就会比较低。但是,如果数据有频繁的插入和删除操作,要想用二分查找,要么每次插入、删除操作之后保证数据仍然有序,要么在每次二分查找之前都先进行排序。无论哪种方法,维护有序的成本都是很高的。
所以,二分查找只能用在插入、删除操作不频繁,一次排序多次查找的场景中。针对动态变化的数据集合,二分查找将不再适用。
4.3 数据量太小不适合二分查找
如果要处理的数据量很小,完全没有必要用二分查找,顺序遍历就足够了。比如在一个大小为 10 的数组中查找一个元素,不管用二分查找还是顺序遍历,查找速度都差不多。只有数据量比较大的时候,二分查找的优势才会比较明显。
但是,有个例外。如果数据之间的比较操作非常耗时,不管数据量大小,都推荐使用二分查找,因为哪怕少比较一次,都可以节省很多时间。比如,数组中存储的是长度超过 300 的字符串,如此长的两个字符串之间比较大小,就会非常耗时。我们需要尽可能地减少比较次数,而比较次数的减少会大大提高性能,这个时候二分查找就比顺序遍历更有优势。
4.4 数据量太大不适合二分查找
二分查找需要依赖数组这种数据结构,而数组为了支持随机访问的特性,要求内存空间连续,对内存的要求比较苛刻。比如,有 1GB 大小的数据,如果希望用数组来存储,那就需要 1GB 的连续内存空间。也就是说,即便有 2GB 的内存空间剩余,但是如果这剩余的 2GB 内存空间都是零散的,没有连续的 1GB 大小的内存空间,那照样无法申请一个 1GB 大小的数组。
所以,太大的数据用数组存储比较吃力,没有数组也就不能用二分查找了。
五、二分查找变形问题
前面介绍了二分查找中最简单的一种情况,即在不存在重复元素的有序数组中查找给定值。下面介绍 4 种常见的二分查找变形问题。
5.1 查找第一个值等于目标值的元素
如果有序数组中存在重复的数据,我们希望找到第一个值等于目标值的元素,该如何用二分查找解决呢?
比如数组 arr = [1,3,4,5,6,8,8,8,11,18] ,其中,arr[5],arr[6],arr[7] 的值都等于 8,是重复的数据,如果查找第一个等于 8 的数据,也就是下标是 5 的元素。
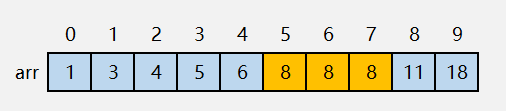
用上面讲的二分查找的代码来实现,首先用 8 与中间值 arr[4] 比较,8 比中间值大,接着在下标 5 至 9 之间查找,8 与 中间值 arr[7] 比较,相等,代码就返回了下标 7。但是,arr[7] 并不是第 1 个等于 8 的元素。
针对这种问题,我们需要对二分查找的代码进行小小的改动。
/**
* 二分查找第1个与目标值相等的元素
*
* @param arr 有序数组
* @param target 要查找的目标数字
* @return 数组包含目标数字,返回第一个等于目标数字的元素位置;数组不包含目标数字,返回 -1
*/
public static int binarySearch(int[] arr, int target) {
int low = 0;
int high = arr.length - 1;
int mid = -1;
while (low <= high) {
mid = (low + high) >> 1;
if (target < arr[mid]) { // 目标值 < 中间值,在左边找
high = mid - 1;
} else if (target > arr[mid]) { // 目标值 > 中间值,在右边找
low = mid + 1;
} else { // 目标值 = 中间值
// 如果当前元素的前一个和目标值也相等,说明它肯定 不是第1个与目标值相等的元素
// 那么 第1个与目标值相等元素 肯定在左边
if (mid != 0 && arr[mid - 1] == target) {
high = mid - 1;
} else {
return mid;
}
}
}
return -1;
}
5.2 查找最后一个值等于目标值的元素
上面查找第 1 个等于目标值的元素理解了,那么查找最后 1 个等于目标值的元素也很容易解决,直接上代码。
/**
* 二分查找最后1个与目标值相等的元素
*
* @param arr 有序数组
* @param target 要查找的目标数字
* @return 数组包含目标数字,返回最后一个等于目标数字的元素位置;数组不包含目标数字,返回 -1
*/
public static int binarySearch(int[] arr, int target) {
int low = 0;
int high = arr.length - 1;
int mid = -1;
while (low <= high) {
mid = (low + high) >> 1;
if (target < arr[mid]) { // 目标值 < 中间值,在左边找
high = mid - 1;
} else if (target > arr[mid]) { // 目标值 > 中间值,在右边找
low = mid + 1;
} else { // 目标值 = 中间值
// 如果当前元素的后一个和目标值也相等,说明它肯定 不是最后1个与目标值相等的元素
// 那么 最后1个与目标值相等元素 肯定在右边
if (mid != arr.length - 1 && arr[mid + 1] == target) {
low = mid + 1;
} else {
return mid;
}
}
}
return -1;
}
5.3 查找第一个大于等于目标值的元素
如果在数组 arr = [3,4,6,7,10] 中查找第一个大于等于 5 的元素,应该是 6。代码如下:
/**
* 二分查找第1个大于等于目标值的元素
*
* @param arr 有序数组
* @param target 要查找的目标数字
* @return 返回第1个大于等于目标值的元素位置
*/
public static int binarySearch(int[] arr, int target) {
int low = 0;
int high = arr.length - 1;
int mid = -1;
while (low <= high) {
mid = (low + high) >> 1;
if (arr[mid] >= target) { // 中间值 >= 目标值
// 如果当前元素是数组第1个元素,或者它前一个元素小于目标值,说明它肯定是第1个大于等于目标值的元素
// 否则,第1个大于等于目标值的元素肯定在左边
if (mid == 0 || arr[mid - 1] < target) {
return mid;
} else {
high = mid - 1;
}
} else { // 中间值 < 目标值,在右边找
low = mid + 1;
}
}
return -1;
}
5.4 查找最后一个小于等于目标值的元素
如果在数组 arr = [3,4,6,7,10] 中查找最后一个小于等于 5 的元素,应该是 4。代码如下:
/**
* 二分查找最后1个小于等于目标值的元素
*
* @param arr 有序数组
* @param target 要查找的目标数字
* @return 返回最后1个小于等于目标值的元素位置
*/
public static int binarySearch(int[] arr, int target) {
int low = 0;
int high = arr.length - 1;
int mid = -1;
while (low <= high) {
mid = (low + high) >> 1;
if (arr[mid] <= target) { // 中间值 <= 目标值
// 如果当前元素是数组最后1个元素,或者它后一个元素大于目标值,说明它肯定是最后1个大于等于目标值的元素
// 否则,最后1个大于等于目标值的元素肯定在右边
if (mid == arr.length - 1 || arr[mid + 1] > target) {
return mid;
} else {
low = mid + 1;
}
} else { // 中间值 > 目标值,在左边找
high = mid - 1;
}
}
return -1;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号