Stochastic Orders 理解和相关运算（_随时补充）

Recall

• 数学里，用\(o\)和\(O\)表示the order the terms.

• \(a_n = o(1)\)：\(a_n \to 0(n \to \infty)\) ，即对任意 $ \epsilon > 0 $,存在正整数 \(N\) ，对所有\(n>N\), 都有 \(|a_n|<\epsilon\).

• \(a_n = O(1)\)： 表示对于某个常数 \(C > 0\)和正整数\(N\)，对于所有\(n>N\)，有 \(|a_n| \leq C\)

• \(a_n= o(b_n)\Leftrightarrow a_n/b_n =o(1).\)

• \(a_n = O(b_n) \Leftrightarrow a_n/b_n = O(1)\)

---

Stochastic order notation

是一种用来表示随机变量序列概率收敛的速记方法。

$ $
【Define】: \(o_p(1)\)（依概率收敛到0)
如果 \(X_n \xrightarrow{P} 0\)，即对于任意 \(\epsilon > 0\)，\(P(|X_n| > \epsilon) \to 0\)，那么我们说 \(X_n = o_p(1)\).

$ $
【Define】: \(O_p(1)\)(依概率有界)

\(X_n = O_p(1)\)，或者说 \(X_n\) 在概率上有界，即如果对于任何 \(\epsilon > 0\)，存在 $C_\epsilon,N_\epsilon $，使得当 \(n>N_\epsilon\) 时，有
\(\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad P(|X_n| > C_\epsilon) \leq \epsilon\)

$ $

---

\(O_p(·)\) 、\(o_p(·)\)的符号理解

[不要觉得上面的第一点if only if没有意义，看起来太自然了.
如果我说：
考虑一个随机变量序列\(X_n\)，其期望为\(E(X_n)= X\), 因此\(X_n= X+o_p(1)\).

proof：根据弱大数定律知, \(X_n\stackrel{p}{\longrightarrow}X\).

这是非常有用的，因为我们不必在方程中引入明确的极限.]

---

[ 再来回顾一下数学里的\(o\)和\(O\)，在华东师大版的数分教材里，特意强调了一点，我们说的 \(a_n = o(1)\)，这里的等式与通常的等式的含义是不同的. 这里等式左边是一个确定性序列（或函数），右边是一个类，中间的等号含义是“属于”]

同理\(o_p\)和\(O_p\)只是用来表示随机变量序列如何收敛（either to zero or a bound ）.也就是我们在定义说的，这只是一种记号.

例如，如果\(X_n= o_p(\frac{1}{n^2})\),那么我们完全也可以说\(X_n = o_p(\frac{1}{n})\),按照我们的需要，我们甚至只断定\(X_n = o_p(1)\).
当然，我们试着看看\(O_p\)的表现.如果\(X_n =O_p(\frac{1}{n})\)....
【注】：这里只用到一个点“\(b_n^{-1}X_n \leq a_n^{-1}X_n = o_p(1)\)”

以上，同时也告诉我们\(O_p(a_n)\)里面的\(a_n\)为什么称作为rate项，可以表示收敛的速度.

这里需要注意，不要觉得\(O\)就不好理解，只因为它不同于小\(o\)趋于0的直接含义.其实也就直接理解为收敛到界的速度呀！\(O_p(1)\)下仍然众生平等，大家都收敛到各自的界.界，那总归有一个相对大的常数，作为它们共同的界，这就和固定的0是一样的了.

上面的例如，越到后面越描述地不够准确，或者说信息量没有被充足地利用起来，我们可以那样说，但就没有那么准确.

---

$ $

现在再来看下面的推广，就很容易接受了：

• \(X_n= o_p(a_n)\Leftrightarrow a_n^{-1}X_n =o_p(1).\) \(a_n\) is the rate;
• \(X_n= O_p(a_n)\Leftrightarrow a_n^{-1}X_n =O_p(1).\) \(a_n\) is the rate.

理解这个，我们就可以对两个量的收敛速度作比较了.
进一步再改写一下

\[X_n= o_p(a_n)\Leftrightarrow X_n = a_n o_p(1) \]

\[X_n= O_p(a_n)\Leftrightarrow X_n = a_n O_p(1) \]

我们发现，根据推广定义，不同的rate还可以写成上述形式.

现在再看上面说的例子，

例如，如果\(X_n= o_p(\frac{1}{n^2})\),那么我们完全也可以说\(X_n = o_p(\frac{1}{n})\),按照我们的需要，我们甚至只断定\(X_n = o_p(1)\).

\(Y_n \overset{p}{\rightarrow} 0, X_n = \frac{1}{n^2}Y_n\)和\(X_n = \frac{1}{n}Y_n\)，当\(n\to \infty\), 对每一个\(Y_n\), 前者小于后者，也就是说前者收敛于0的速度更快.

---

\(O_p\)和\(o_p\)的关系

了解了所谓stochastic orders的含义，我们进一步看看一些常用的组合运算结果.(😄)

Remark:

• 第1个大家按照定义证明，没有大问题.就当检验一下是否完全理解定义...（这个结果更好体现出stochastic orders notation的意义所在...）

• 即依概率趋于0的随机变量,一定依概率有界.看着是很自然的.

• 依概率有界项乘上依概率收敛到0的项等于以概率收敛到0.依概率有界项乘上依概率有界项等于依概率有界.

• 依概率有界项加上依概率收敛到0的项等于依概率有界.

• 理解了上面的rate项，直接得出.

$ $
下面依次给出证明：

---

证明前，我们回顾一下定义：

• \(X_n = o_p(1)\):\(X_n \xrightarrow{P} 0\)，【依概率收敛定义】：\(\forall \delta >0, \lim\limits_{n\to \infty} P(|X_n|>\delta ) = 0.\)

• \(X_n = O_p(1)\):
  \(\forall \epsilon >0,\exists C_\epsilon, N_\epsilon, s.t. P(|x_n|>C_\epsilon)\leq \epsilon.\)

---

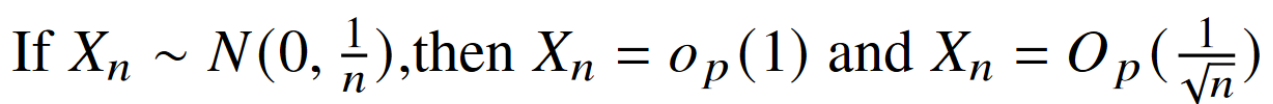
(1) 考虑对\(\forall \delta\)，

\(\quad P(|X_n|>\delta)\)
= \(P(|N(0,\frac{1}{n})|>\delta)\)
= \(P(\frac{1}{\sqrt n}|N(0,1)|>\delta)\)
= \(P(|N(0,1)|>\sqrt n\delta)\)
= \(2(1-\Phi(\sqrt n\delta))\)

当\(n \to \infty\), \(\Phi(\sqrt n\delta) \to 1\) ,\(P(|X_n|>\delta) \to 0\).
\(X_n = o_p(1)\)得证.

(2) 考虑对\(\forall \epsilon\)，

\(\quad P(\sqrt n|X_n|>C_\epsilon)\)
=\(P(\sqrt n |N(0,\frac{1}{n})|>C_\epsilon)\)
=\(P(|N(0,1)|>C_\epsilon)\)
=\(2(1-\Phi(C_\epsilon))\).
当\(C_\epsilon\) 满足:
\(2(1-\Phi(C_\epsilon))\leq \epsilon\).
我们就有：
\(P(\sqrt n|X_n|>C_\epsilon) \leq \epsilon.\)
\(X_n = O_p(\frac{1}{\sqrt n})\)得证.

Remark:
事实上，我们可以直接有：\(X_n = O_p(\frac{1}{\sqrt n}) \Rightarrow X_n = o_p(1)\)
我们来证明一下：
对\(\forall \delta>0\)，我们有\(\forall \epsilon>0\), \(\exists C_\epsilon\)，对足够大的\(n\)，有，
\(\quad P(|X_n|>\delta)\)
\(=P(|X_n|>\delta, \sqrt n|X_n|>C_\epsilon)+P(|X_n|>\delta, \sqrt n|X_n|\leq C_\epsilon)\)
\(\leq P(\sqrt n|X_n|>C_\epsilon)+0\)
\(\leq P(\sqrt n|X_n|>C_\epsilon)\)
\(\leq \epsilon\)

---

---

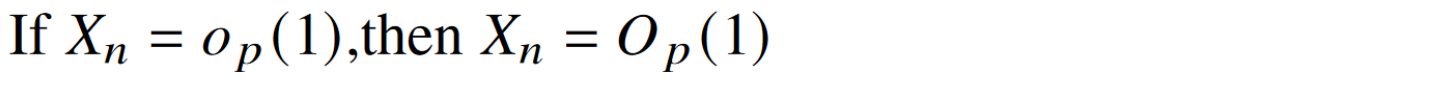
按\(\epsilon-N\)语言的极限定义，\(X_n = o_p(1)\Longleftrightarrow \forall \delta,\epsilon (>0),\exists N_{\epsilon \delta}, s.t. P(|x_n|>\delta)\leq \epsilon.\)

即\(X_n = o_p(1)\Longrightarrow P(|x_n|>C)\leq \epsilon\)，C是某个常数，for all \(\epsilon>0 \Longrightarrow X_n = O_p(1).\)

---

---

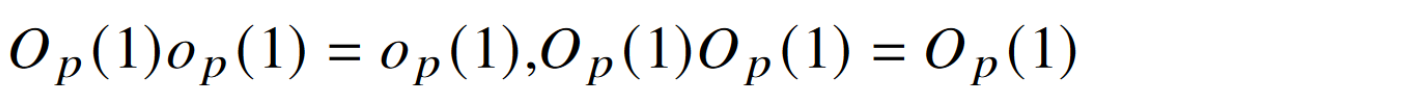
(1) 设\(X_n= O_p(1), Y_n = o_p(1)\)，对\(\forall \delta>0\)，我们有\(\forall \epsilon>0, \exists\xi>0\)，对足够大的\(n\)，有，

\(\quad P(|X_nY_n|> \delta)\)
\(=P(|X_nY_n|> \delta,|Y_n| >\xi)+P(|X_nY_n|> \delta,|Y_n| \leq \xi)\)
\(\leq P(|Y_n| >\xi)+P(|X_n|> \delta/\xi)\)
\(\leq \frac{\epsilon}{2}+\frac{\epsilon}{2} = \epsilon\)

即\(X_nY_n=o_p(1)\)，命题得证.

(2) 设\(X_n= O_p(1), Z_n = O_p(1)\)，对\(\forall \epsilon>0\)，\(\exists C_{\epsilon1} C_{\epsilon2}\),使得对足够大的\(n\)，有

\(\quad P(|X_nZ_n|> C_{\epsilon1} C_{\epsilon2})\)
\(\leq P(|X_n|>C_{\epsilon1} \bigcup |Z_n|> C_{\epsilon2})\)
\(\leq P(|X_n|>C_{\epsilon1})+P(|Z_n|> C_{\epsilon2})\)
\(\leq \frac{\epsilon}{2}+\frac{\epsilon}{2} = \epsilon\)

---

---

设\(X_n= O_p(1), Y_n = o_p(1)\)，对\(\forall \epsilon>0\)，我们有\(\exists C_\epsilon\)，对足够大的\(n\)，有，

\(\quad P(|X_n + Y_n|> C_\epsilon)\)
\(\leq P(|X_n|+|Y_n|> C_\epsilon)\)
\(\leq P(|X_n|>\frac{C_\epsilon}{2} \bigcup |Y_n|> \frac{C_\epsilon}{2})\)
\(\leq P(|X_n|>\frac{C_\epsilon}{2})+P(|Y_n|> \frac{C_\epsilon}{2})\)
\(\leq \frac{\epsilon}{2}+\frac{\epsilon}{2} = \epsilon\)

---

---

(1)
\(O_p(a_n)o_p(b_n)＝a_nO_p(1)b_no_p(1) = a_nb_n O_p(1)o_p(1) = a_nb_no_p(1)=o_p(a_nb_n)\)
(2)
\(O_p(a_n)O_p(b_n)＝a_nO_p(1)b_nO_p(1) = a_nb_n O_p(1)O_p(1) = a_nb_nO_p(1)=O_p(a_nb_n)\)

---

---

$ $
$ $
【笔者说明】：证明基于定义，难点只在关于联合概率不等式.
这里说到概率不等式，在计算随机变量概率收敛速度比较常用的马尔可夫不等式，在这里也给出：
\(i_A P(X \in A)\leq E(\varphi(x))\)
其中函数\(\varphi\geq 0, i_A = inf\{\varphi(x): x\in A\}\).

例如我们熟悉的切比雪夫不等式：
\(P(|X|\geq a) \leq \frac{EX^2}{a^2}\)

当\(X\)非负时，更有：
\(P(X\geq a) \leq \frac{EX}{a}\)

$ $$ $
$ $
$ $
$ $
参考文章：

1. https://blog.csdn.net/u011375991/article/details/130813883
2. https://zhuanlan.zhihu.com/p/676370426