指数分布和伽马分布介绍

指数分布

指数分布的密度函数和分布函数

首先，让我们给出参数为\(\lambda\)的指数分布密度函数图

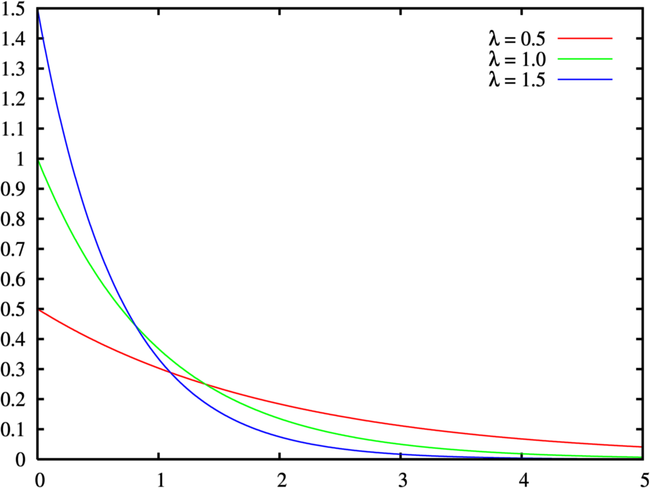
\(\qquad\) 从图中可以看到，指数分布是一种偏态分布(对比于正态分布).

\(\qquad\)由于指数分布随机变量只可能取非负实数，所以指数分布常被用作各种“寿命”分布，电话的通话时间、随机服务系统中的等待时间等都可假定服从指数分布.指数分布可在可靠性与排队论中有着广泛的应用.

\(\qquad\)这里给出如何记忆指数分布的密函函数和分布函数:建议记密度函数，一般密度函数考察会多一点~但是其实知道密度函数不一定推出分布函数，但知道分布函数可以直接算出密度函数，但你得承认，密度函数比分布函数好记，这里指数分布的密度函数是

\[f(x)= \lambda e^{-\lambda x} \]

因为\(f(x)\)本来就是因为可以积分得到\(F(x)\)，所以前面的\(\lambda\)是求导的产物.

伽马分布

\(\qquad\)首先我们介绍一个函数(重点介绍，一直学一直忘（无语...😢：

\[\Gamma (\alpha)= \int _0 ^\infty x^{\alpha -1}e^{-x} dx \]

其中\(\alpha>0\).这个函数叫做伽马函数.

\(\qquad\)现在我们从根源记住伽马函数...
\(\qquad\)伽马函数的设定完全可以等价于解决一个插值问题：找到一个平滑的曲线连接点“（x,y）”，其中y = (x-1)!, x是正整数值.

\(\qquad\)首先什么是阶乘函数？

\(\qquad\)我们当然知道阶乘是什么了：

\[n! = n*(n-1)*(n-2)* \cdots *1 \]

阶乘函数就是带有上述阶乘运算的函数.y = (x-1)!就是一个阶乘函数.

\(\qquad\)再回到我们伽马函数，其实就是说，我们知道阶乘函数是仅对于离散点定义，但是我们希望连接起这些离散的点，也就是说将阶乘函数拓展到所有复数上.

\(\qquad\)但很显然阶乘的简单公式不能直接用于小数值，因为它仅在\(x\)是整数时才有效。因此，数学家一直在寻找“什么样的function将这些点平滑地连接起来，并为我们提供所有实际值的阶乘？”

\(\qquad\)而事情的转机就在此，欧拉他发现了伽马函数.

\[\Gamma (\alpha)= \int _0 ^\infty x^{\alpha -1}e^{-x} dx \]

\(\qquad\)上面的公式用于找到\(\alpha\)在任何实数值的Gamma函数的值.也就是说伽马函数解决了我们的问题，此刻再回顾一下，什么问题？...

-----标答-----：我们希望找到一拟合曲线，它连接着点【which is"每个正整数点x上f(x)= （x-1）！"】

\(\qquad\)好了，以上的了解是为了让读者深刻体会伽马函数的意义，其实就是直接记住它的性质，读者现在可以停下来想想伽马函数什么性质来着？...

\[ \Gamma (\alpha) = (\alpha -1) ! =(\alpha-1)\Gamma(\alpha-1) \]

这里特别需要注意，第二个等号右边是一个记号，以便于自己理解，因为阶乘运算只在整数点，一定注意.

不要觉得迷糊，到这里，再顺一遍我们的逻辑，应该没什么问题~加油...

---

这里我们开始详细看看Gamma函数：

\[\Gamma (\alpha)= \int _0 ^\infty x^{\alpha -1}e^{-x} dx \]

为什么选择这两项,欧拉是发现自然数e的那个人，因此他必须做很多实验，将e与其他函数相乘才能找到当前形式.不敢想象...

\(\qquad\)但可以看到当\(x\to \infty\)时，多项式项快速增长和指数项快速下降.

这里可以参考：
https://zhuanlan.zhihu.com/p/147583667
也是本随笔的主要参考文章.

\(\qquad\)总之，也就是说伽玛函数会收敛到有限值.

\(\qquad\)接下来我们理论来分析伽马函数：
1.利用分部积分法，可以直接得到递推公式：

\[\Gamma (\alpha) = (\alpha - 1)\Gamma(\alpha-1) \]

这里的推导不难，建议读者自己证明一下，是简单的，我说简单就是真的简单，因为本人是一个十足的证明恐惧选手，数学里最明显的弱点...我恨

2.\(\Gamma(1)= 1\)

3.\(\Gamma(n)= (n-1)!\)
注3：不要以为这个很简单，这就是数学里的绝对细节...3的结果依靠于2.

现在我们可以自信的说，我们会很容易记住伽马分布的密度函数.

大标题给了上面的自信，其实这一小节的标题叫做：

使用Gamma函数的属性，显示Gamma分布的PDF积分为1.

\[p(x) = \left\{ \begin{aligned} &\frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}, && x \geq 0 \\ &0, && x < 0 \end{aligned} \right. \]

\(\qquad\)现在你应该可以轻易记住这个分布的密度函数了，因为Gamma函数的良好性质，这个函数的积分是1.

\(\qquad\)现在我们一起来看看，分式那一项完全不需要考虑拿出积分外. 可以看到，\(x^{\alpha-1}e^{-\lambda x}\)类似于伽马函数的被积项，回顾Gamma函数啊，形象记忆就是有多项式的升和指数的降，可以看到和这里的形式很像，我们具体来看看，只有自己做一遍才能记得牢，事实上，在写之前我已经推了一遍了，但我又忘了...到底要怎么记（😠）

\[\int_0^\infty x^{\alpha-1}e^{-\lambda x} dx = \frac{1}{\lambda^{\alpha}} \int_0^\infty \lambda^{\alpha} x^{\alpha-1} e^{-\lambda x} d\lambda x= \frac{1}{\lambda^{\alpha}} \Gamma(\alpha) \]

\(\qquad\)right， 这就是为什么\(p(x)\)里面会有\(\frac{\lambda^ \alpha} {\Gamma (\alpha)}\).

\(\qquad\)ok,伽马函数介绍基本就到这里，至于还有比较重要的待证明的：

\[\Gamma(\frac{1}{2}) = \sqrt{\pi} \]

这里后面有需要补充！！

---

\(\qquad\)现在我们再看这两个分布，当\(\alpha =1\)时，伽马分布就是指数分布.现在再看伽马分布，\(G(\alpha, \lambda)\)，看到上面的指数分布的图，它整体形状是不会变的（呈现一个单调下降的趋势），\(\lambda\)的大小是决定趋势的大小，也就是图形的尺寸.