Control of Mobile Robots 学习笔记（一）Introduction

《Control of mobile robot》是Gatech的Dr. Magnus Egerstedt在Coursera上发布的一个公开课(现在好像没在Coursera了，这位老师也不在Gatech了)。之前没有自主移动机器人方面的基础，学习的同时记录一下。

课件是从github上下载的。

在Module1（Introduction）中介绍了

• What is control theory?
• Dynamic model
• Cruise controller (定速器)
• Controller design basics and PID controller

What is control theory?

首先知道一些基本的术语：

• System = Something that changes over time （比如机器人）
• State = Representation of what the system is currently doing （描述系统当前的状态）
• Dynamics = Description of how the state changes （描述这些状态怎么变化）
• Control = Influence that change （影响这个变化）

一个系统如下图所示：

其中，x是系统状态，u是控制量，y是系统输出。r是参考状态

Dynamic model（动力学模型）

控制的核心问题是如何选择输入量u，使得系统

• 稳定
• 轨迹跟踪
• 鲁邦
  ...

用什么模型描述系统的动力学模型呢？预测模型

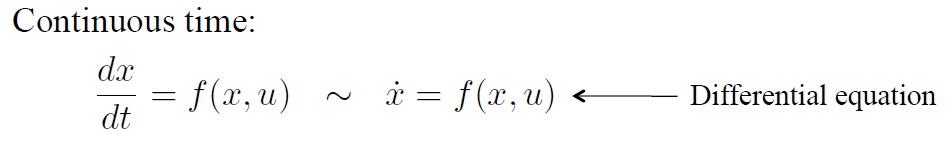
用微分方程描述系统的变化；状态的变化和状态以及控制量有关。

Cruise controller

（定速器或者Car model）

假设不考虑汽车的转弯，一直在直线行走，在此场景下，State是汽车的速度，Input是油门或者刹车，Dynamics是速度关于时间的变化情况

目标是将汽车根据参考速度(r)行走；即，t->∞时，x->r。e->0(e = r-y)

由于状态x是速度，求导得加速度a。根据上图式推导，得 derivartive (x) = c/m * u;

Controller design basics and PID controller

那么，有了Car model， 下一步是怎么设计u（控制器），使得汽车按照参考速度稳定行走？

Attempt 1: Bang Bang Controller
u=umax， if e > 0
u=0， if e = 0
u=-umax， if e < 0

当e > 0时，即 r-x > 0，汽车实际速度还没到目标速度，这时全速前进。反之，全速反方向移动。效果图如下：

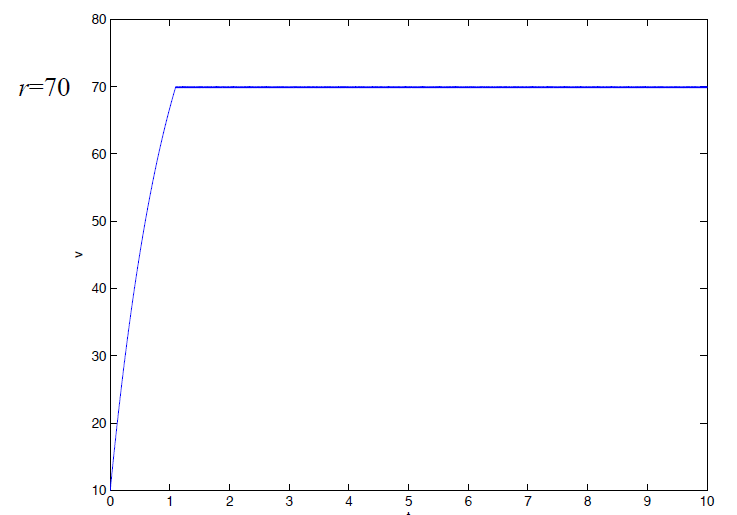
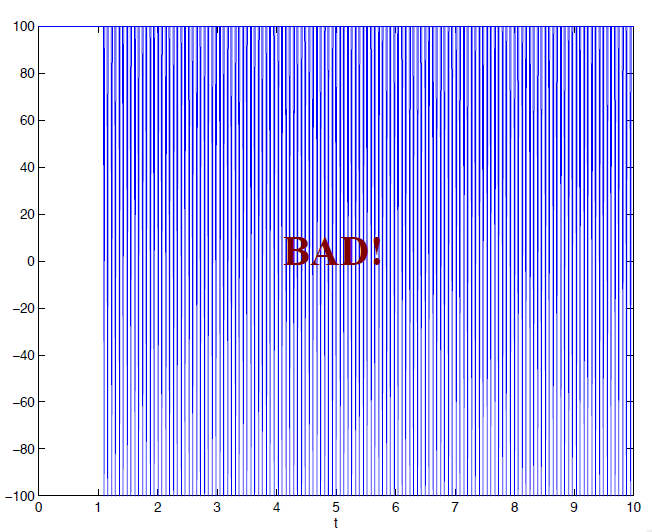
结果是能到参考速度，但是，控制量在最高和最低点再短时间内一直横跳。这个不平滑，不是理想的控制方法。

Attempt 2： P-regulator （P控制器）
u = ke

误差越小，控制量也越小，符合直观认知。

实际效果图如下：

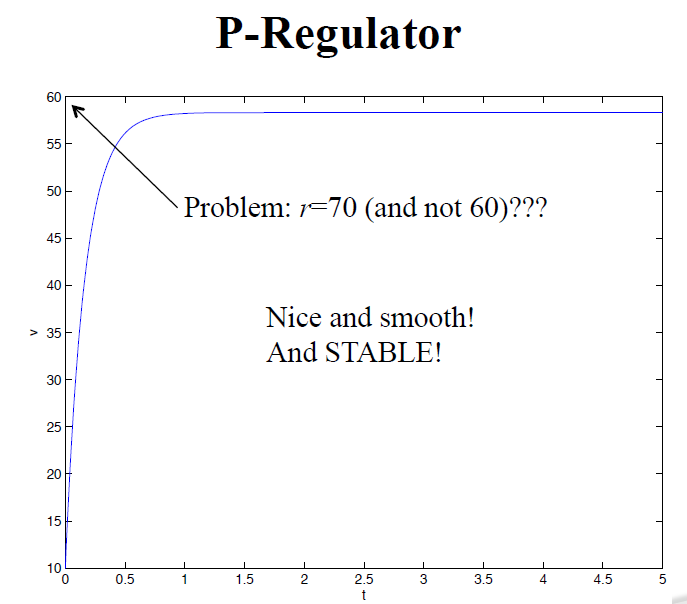
速度以平滑，稳定的到60左右，但是参考速度是70. （关于P控制器为什么到不了参考值，PPT有证明过程）

Attempt 3： PID controller

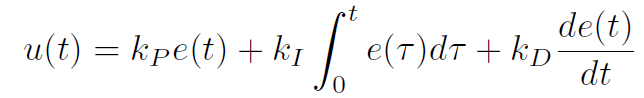
PID 是应用最广泛的底层控制器。通常按照经验选择三个系数Kp, Ki, Kd。 该控制器的结果符合平滑，稳定的要求且能够到达参考值。

总结

首先，介绍了系统的建模（状态，控制，动力学），之后对动力学的预测模型的推导，通过Car model来距离，关于car model的稳定速度控制问题，设计了bang bang controller，p-controller和PID controller，分析了结果。