03 二叉树相关的经典编程题
- 第三章
- 3-1 实现二叉树的3种遍历方式(非递归)
- 3-2 打印二叉树的边界节点
- 3-3 二叉树的序列化与反序列化
- 3-4 二叉树的Morris(莫里斯)遍历(需要时查看书籍)
- 3-5 在二叉树中找到累加和为指定值的最长路径长度
- 3-6 找到二叉树中最大搜索二叉树
- 3-7 找到二叉树中最大的拓扑结构
- 3-8 二叉树的按层打印以及ZigZag打印
- 3-9 调整搜索二叉树中的二个错误节点
- 3-10 判断t1是否存在与t2相同的拓扑结构
- 3-11 判断t1是否存在与t2相同的子树
- 3-12 判断二叉树是否为平衡二叉树
- 3-13 根据后序数组重建搜索二叉树
- 3-14 二叉树2个节点的最近公共祖先(LCA问题)
- 3-15 二叉树节点之间的最大距离问题
- 3-17 2种遍历序列构造树的的系列问题
- 3-18 统计和生成所有的二叉树
- 3-19 派对最大的欢乐值
- 补充题目
- 用到的数据结构方法
- 思考
- 树的基本代码
- 参考资料
第三章
3-1 实现二叉树的3种遍历方式(非递归)
三种遍历方式preorder, inorder, postorder是所有树相关题目的基础。
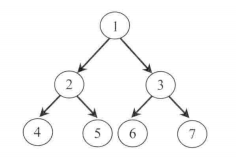
非递归实现(手动模拟,理清思路再写)
先序遍历:
step1: 申请一个stack,将头节点压入栈。
step2:进行一次出栈,打印出栈节点值,然后先压入当前出栈节点的右节点,然后再压入左节点。
重复step2直到stack为空(while循环)
中序遍历(直观上有点难以理解):
step1: 申请一个stack,让遍历指针cur指向头节点。
step2: 判断cur的左节点是否为空:
- 不为空(说明左边有路走),则将cur指向的节点压入栈中,令cur = cur->left.(每个进栈的节点右边都没有探索)
- 为空(说明该子树左分支已经走完),则出栈一个节点,打印该节点值,并令cur指向出栈节点的right。(探索新的节点的右分支)
重复step2,直到栈为空。
后序遍历
1 使用2个栈(s1,s2)实现
基本思路:
step1: 将头节点压入s1
step2: 从s1中弹出一个节点,
- 首先将该节点压入s2
- 然后检查该节点左边是否为空,不空从压入s1,再检查右边是否为空,不空也压入s1(注意压入s1必须先左后右边,反过来出s1进s2,最终出s2还是先左后右)
step3: 重复上述过程,直到栈s1为空。
step4:依次出栈s2的结果就是树的后序遍历。
2 使用一个栈实现
基本思路:
step1:设定2个指针,h直线最近弹出并打印的节点,c指向当前栈顶节点
step2:
- 情况1:如果当前栈顶节点c的左孩子不为null,并且h不等于c的左孩子也不等于c的右孩子,则将c的左孩子压入栈。(说明栈顶节点的左右子树都没有遍历)
- 情况1如果不满足:则再判断 当前栈顶节点c的右孩子不为null,并且h不等于不等于c的右孩子,则将c的右边孩子压入栈(说明栈顶节点的右子树没有处理)
- 情况1,2都不满足,弹出该节点并打印数值(当前栈顶节点左右子树都已经遍历)。
重复step2直到栈为空
三种遍历方式非递归实现
- 先序遍历:循环中每次出栈,打印,右节点入栈并且左节点入栈
- 中序遍历: 只要左子树不为空就一直入栈,否则出栈打印,并指向出栈节点的右侧。
- 后序遍历: 关键在于记录最近打印节点的指针。
#include<bits/stdc++.h>
using namespace std;
struct Node{
int v;
Node* left;
Node* right;
};
void buildTree(Node* &root,int value){
if(value == 0){
root = NULL;
return;
}
int fa,lch,rch;
cin >> fa >> lch >> rch;
root = new Node();
root->v = value;
buildTree(root->left,lch);
buildTree(root->right,rch);
}
void preorder(Node* root){
if(root == NULL)
return;
printf("%d\n",root->v);
preorder(root->left);
preorder(root->right);
}
void preorder_another(Node* root){
if(root == NULL)
return;
stack<Node*> s1;
s1.push(root);
bool first = true;
while(!s1.empty()){
root = s1.top();
s1.pop();
//step1:打印节点
if(first){
printf("%d",root->v);
first = false;
}
else
printf(" %d",root->v);
// step2:右节点入栈
if(root->right != NULL)
s1.push(root->right);
// step3:左节点入栈
if(root->left != NULL)
s1.push(root->left);
}
printf("\n");
}
void in_order_another(Node* cur){
stack<Node*> s1;
bool first = true;
// 注意循环条件判断,cur != NULL只有第一次用到
while(!s1.empty() || cur != NULL){
// 左子树不为空
if(cur != NULL){
s1.push(cur);
cur = cur->left;
}
else{
// 取出节点并打印,遍历右子树
cur = s1.top();
s1.pop();
if(first){
printf("%d",cur->v);
first = false;
}
else
printf(" %d",cur->v);
cur = cur->right;
}
}
printf("\n");
}
void postorder_another(Node* root){
stack<Node*> s1;
bool first = true;
Node* h = root; // 最近弹出并打印的节点
Node* cur = NULL;
s1.push(root);
while(!s1.empty()){
cur = s1.top();
// 判断左边是否已经遍历
if(cur->left != NULL && cur->left != h && cur->right != h){
s1.push(cur->left);
// 判断右边是否遍历
}else if(cur->right != NULL && cur->right != h) {
s1.push(cur->right);
}else{ // 左右皆遍历
Node* tmp = s1.top();
s1.pop();
if(first){
printf("%d",tmp->v);
first = false;
}
else
printf(" %d",tmp->v);
h = tmp; // 保留上次打印的节点指针
}
}
printf("\n");
}
int main(){
int n,root;
cin >> n >> root;
Node* r;
buildTree(r,root);
preorder_another(r);
in_order_another(r);
postorder_another(r);
return 0;
}
3-2 打印二叉树的边界节点
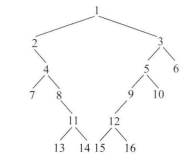
边界节点的定义方式1:头节点与叶节点为边界节点,每一层的节点的最左边与最右边的节点。
示例:1,2,4,7,11,13,14,15,16,10,6,3
边界节点的定义方式2:头节点与叶节点为边界节点,树左右边界延伸下去的路径为边界节点。
示例:1,2,4,7,13,14,15,16,10,6,3
**要求: **时间复杂度为O(N),额外空间复杂度为O(h)。
常识:叶节点通过左右节点都为空判断其为空指针。
方式1基本思路:
概述:需要对整个树遍历3次,定义一个大小为 树的高度*2 的指针数组用于存储整棵树的边界节点指针。
step1: 写一个递归函数获取树的高度(第一次遍历)
step2:按照前序遍历的思想,写一个递归函数给指针数组赋值(将打印处修改为赋值,第二次遍历):
- 左边界节点:每层第一个访问的节点(l,0处为空直接赋值)
- 右边界节点: 每层最后一个访问的节点(l,1处一直赋值就行)
step3:
- 1)打印存储在数组中的左边界节点
- 2)打印与数组中节点不同但是是叶节点的值
- 叶节点值的打印,采用前序遍历,但是对打印的节点做出以下要求:
- 该节点左右指针为空,且该节点的指针没有存储在之前的指针数组中
- 叶节点值的打印,采用前序遍历,但是对打印的节点做出以下要求:
- 3)打印存储在指针数组中的右边界节点,注意对于与左边界重复的节点不需要打印。
方式2基本思路(不是太理解)
print的设置来确定节点是否为边界节点
-
叶节点一定是边界节点
-
左边界的打印遵循前序遍历的思想,节点左边没有孩子可能是边界节点。
-
右边界的打印遵循后序遍历的思想,节点右边没有孩子可能是边界节点
-
注意点:当头节点有一个节点为null需要递归调用,因为这棵树也可能是棒状
代码:
#include <bits/stdc++.h>
using namespace std;
#define N 1000001
vector<int> Nodes[N];
int getH(int cur){
if(cur == 0)
return 0;
int lh = getH(Nodes[cur][0]);
int rh = getH(Nodes[cur][1]);
return 1+max(lh,rh);
}
void preorder_first(int cur,int deep,int saved[][2]){
if(cur == 0)
return;
if(saved[deep][0] == -1)
saved[deep][0] = cur;
saved[deep][1] = cur;
preorder_first(Nodes[cur][0],deep+1,saved);
preorder_first(Nodes[cur][1],deep+1,saved);
}
void preorder_second(int cur,int deep,int saved[][2]){
if(cur == 0)
return;
if(Nodes[cur][0] == 0 && Nodes[cur][1] == 0){
if(cur != saved[deep][0] && cur != saved[deep][1])
cout << " " << cur;
}
preorder_second(Nodes[cur][0],deep+1,saved);
preorder_second(Nodes[cur][1],deep+1,saved);
}
void printEdge(int saved[][2],int height){
// step1:打印所有左边界节点
for(int i = 0;i < height;++i){
if(i == 0)
cout << saved[i][0];
else
cout << " " << saved[i][0];
}
// step2:打印不是左边界也不是右边界的叶节点
preorder_second(saved[0][0],0,saved);
// step3:打印右边界节点,注意与左边界节点相同不用重复打印!!!!
for(int i = height-1;i > 0;--i){
if(saved[i][1] != saved[i][0])
cout << " " << saved[i][1];
}
}
//===================================================================
void printLeftEdge(int cur,bool print){
if(cur == 0)
return;
// 注意这里条件不能拆分
if(print || (Nodes[cur][0] == 0 && Nodes[cur][1] == 0))
cout << cur << " ";
printLeftEdge(Nodes[cur][0],print);
printLeftEdge(Nodes[cur][1],print && Nodes[cur][0] == 0 ? true:false);
}
void printRightEdge(int cur,bool print){
if(cur == 0)
return;
// 注意这里条件不能拆分
printRightEdge(Nodes[cur][0],print && Nodes[cur][1] == 0 ? true:false);
printRightEdge(Nodes[cur][1],print);
if(print || (Nodes[cur][0] == 0 && Nodes[cur][1] == 0))
cout << cur << " ";
}
void printEdge2(int cur){
if(cur == 0)
return;
cout << cur << " ";
// 左右子树都不为空,则先左后右
if(Nodes[cur][0] != 0 && Nodes[cur][1] != 0){
printLeftEdge(Nodes[cur][0],true);
printRightEdge(Nodes[cur][1],true);
}else{ // 根据左右子树递归
if(Nodes[cur][0] != 0)
printEdge2(Nodes[cur][0]);
else
printEdge2(Nodes[cur][1]);
}
}
int main()
{
int n,root;
scanf("%d%d",&n,&root);
int fa,lch,rch;
for(int i = 0;i < n;++i){
cin >> fa >> lch >> rch;
Nodes[fa].push_back(lch);
Nodes[fa].push_back(rch);
}
int height = getH(root);
int saved[height][2];
fill(saved[0],saved[0]+2*height,-1);
preorder_first(root,0,saved);
printEdge(saved,height);
cout << endl;
printEdge2(root);
return 0;
}
3-3 二叉树的序列化与反序列化
基本思想:无论是序列化,还是反序列化都是在原有先序遍历与层序遍历的算法上修改。
import java.util.*;
public class TreeSerial {
static int [] left = new int[1000001];
static int [] right = new int[1000001];
static StringBuilder pre_s = new StringBuilder();
static StringBuilder level_s = new StringBuilder();
static void preorder(int root){
if(root == 0){
pre_s.append("#!");
return;
}
pre_s.append(root).append("!");
preorder(left[root]);
preorder(right[root]);
}
static void levelorder(int root){
Queue<Integer> tmp_q = new LinkedList<Integer>();
tmp_q.add(root);
while (!tmp_q.isEmpty()){
int cur= tmp_q.poll();
if(cur == 0)
level_s.append("#!");
else{
level_s.append(cur).append("!");
tmp_q.add(left[cur]);
tmp_q.add(right[cur]);
}
}
}
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int n,root;
n = input.nextInt();
root = input.nextInt();
int fa,lch,rch;
for(int i = 0;i < n;++i){
fa = input.nextInt();
lch = input.nextInt();
rch = input.nextInt();
left[fa] = lch;
right[fa] = rch;
// System.out.printf("%d %d %d\n",fa,lch,rch);
}
preorder(root);
System.out.println(pre_s.toString());
levelorder(root);
System.out.println(level_s.toString());
}
}
3-4 二叉树的Morris(莫里斯)遍历(需要时查看书籍)
要求:完成三种遍历的时间复杂度为O(N),空间复杂度为O(1)
基本思想:利用了树中的空指针
3-5 在二叉树中找到累加和为指定值的最长路径长度
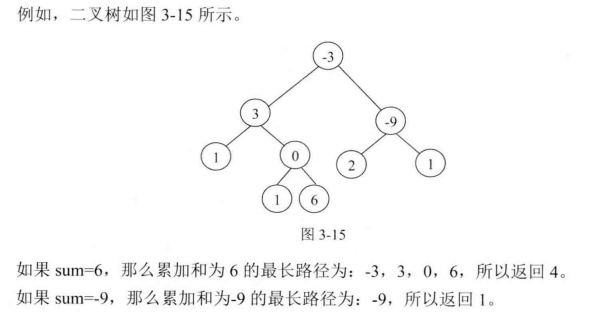
题意:给定一颗二叉树和一个整数 sum,求累加和为 sum 的最长路径长度。路径是指从某个节点往下,每次最多选择一个孩子节点或者不选所形成的节点链。
这道题与数组中找到累计和为指定值的子数组的最长长度是非常相似。
核心思想:
基本思路:
step1:定义一个hashmap,其key值为从头节点到当前节点的路径和,value是该值第一次出现的深度。
- 首先插入键值对(0,-1),表示和为0不需要任何节点(根节点算作0层,如果根节点算作1层,则插入(0,0)
step2:对树进行前序遍历,定义递归函数
-
- 将当前的累计值放入到hash表中,如果没有的话。
-
2)查看sum-k是否在Hash表中。sum-k在,尝试更新路径最大长度
-
- 访问左子树,访问右子树
-
- 如何hash表中存在当前累加值,且表中深度等于当前深度,则移除
-
- 返回当前最大路径
总结:这道题目可以看成数组中找到累计和为指定值的子数组的最长长度的多路径版本,通过动态的维护hashmap从而高效的判断每条路径的最大长度。而在之前的数组中,hashmap实际上是静止不变的,而这道题是动态变化的,从额外空间复杂度也可以看出来,hashmap最多存储的节点数就是树的高度,这一点尤其需要注意。
时间复杂度:O(n) 额外空间复杂度:O(h),其中h为树的高度。
#include <bits/stdc++.h>
#define MAXN 200001
using namespace std;
struct Node{
int v;
vector<int> child;
}nodes[MAXN];
unordered_map<int,int> treemap;
int maxlen = 0;
// cur:当前节点位置,sum:目标值,cur_sum:当前值,deep:深度
void preorder(int cur,int sum,int cur_sum,int deep){
if(cur == 0){
return;
}
cur_sum += nodes[cur].v;
// 判断当前节点能够成为复合要求的路径的终端节点
if(treemap.find(cur_sum-sum) != treemap.end()){
int len = deep-treemap[cur_sum-sum];
maxlen = max(maxlen,len);
}
// 存储累加和到hashmap
if(treemap.find(cur_sum) == treemap.end()){
treemap[cur_sum] = deep;
}
preorder(nodes[cur].child[0],sum,cur_sum,deep+1);
preorder(nodes[cur].child[1],sum,cur_sum,deep+1);
// 删除累加和
if(treemap.find(cur_sum) != treemap.end() && treemap[cur_sum] == deep){
treemap.erase(cur_sum);
}
}
int main(){
int n,root;
int fa,lch,rch,val;
int sum;
scanf("%d %d",&n,&root);
for(int i = 0;i < n;++i){
scanf("%d %d %d %d",&fa,&lch,&rch,&val);
nodes[fa].v = val;
nodes[fa].child.push_back(lch);
nodes[fa].child.push_back(rch);
// printf("%d %d %d %d\n",fa,lch,rch,val);
}
scanf("%d",&sum);
// 初始化treemap
treemap[0] = 0;
preorder(root,sum,0,1);
printf("%d\n",maxlen);
return 0;
}
3-6 找到二叉树中最大搜索二叉树
描述:给定一颗二叉树,已知其中所有节点的值都不一样,找到含有节点最多的搜索二叉子树,输出该子树总节点的数量。搜索二叉树是指对于二叉树的任何一个节点,如果它有儿子,那么左儿子的值应该小于它的值,右儿子的值应该大于它的值。输出该子树总结点的数量,时间复杂度为O(N),空间复杂度为O(h)。
基本思想:
step1:构造一个数据结构record,用于存储以当前节点为根节点的子树所包含的最大BST的
- 1)根节点指针
- 2)所有节点最大值
- 3)所有节点最小值
- 4)树中节点的数量
step2: 编写递归函数,参数是当前节点的指针cur,返回值为record
- 1)如果空指针,设置好record直接返回(技巧性设置:将最大值设为最小值,最小值设为最大值)
- 2)遍历左子树,获取左子树返回的 left_record
-
- 遍历右子树,返回右子树返回的 right_record
-
- 分二种情况讨论:
- 左右子树与右子树与当前节点构成BST,设置好新的record返回(细节注意,与1)处自洽)
- 左右子树与右子树无法当前节点构成BST,返回 right_record与 left_record中节点多的一个。
代码实现:
#include <bits/stdc++.h>
#define maxn 1000001
#define MAXV 20000000
#define MINV -1
using namespace std;
struct node{
int data; //数据域,本题可以不用数据区域
vector<int> child; //指针域,存放所有子结点的下标,子节点的个数无法预知,使用动态数组能很好的处理这个问题
} Node[maxn]; //直接定义节点数组
struct Record{
int maxv; // 该子树包含的最大BST的最大值
int minv; // 该子树包含的最大BST的最大小值
int len; // 该子树包含的最大BST的节点数
int root_index; // 该子树的根节点index
};
Record postorder(int cur){
// 取出数据方便后面比较
int fa = Node[cur].data;
int lch = Node[cur].child[0];
int rch = Node[cur].child[1];
Record record;
// 空节点,注意空间的记录最大最小值赋值要与情况1实现自洽
if(fa == 0){
record.maxv = MINV;
record.minv = MAXV;
record.len = 0;
record.root_index = 0;
return record;
}
Record leftTreeRecord = postorder(lch);
Record rightTreeRecord = postorder(rch);
// 情况1:当左右子树都是BST,并且满足节点<右子树的最小值 且 节点>左子树的最大值
if(leftTreeRecord.root_index == lch && rightTreeRecord.root_index == rch)
if(fa > leftTreeRecord.maxv && fa < rightTreeRecord.minv){
record.maxv = max(fa,rightTreeRecord.maxv);
record.minv = min(fa,leftTreeRecord.minv);
record.len = leftTreeRecord.len+rightTreeRecord.len+1;
record.root_index = fa;
return record;
}
// 情况2/3:返回左子树的最大BST记录/返回右子树的最大BST记录
return leftTreeRecord.len > rightTreeRecord.len ? leftTreeRecord : rightTreeRecord;
}
int main(){
int n,root;
scanf("%d %d",&n,&root);
int fa,lch,rch;
for(int i = 0;i < n;++i){
scanf("%d %d %d",&fa,&lch,&rch);
Node[fa].data = fa;
Node[fa].child.push_back(lch);
Node[fa].child.push_back(rch);
}
Record record = postorder(root);
printf("%d\n",record.len);
return 0;
}
时间复杂度O(N), 空间复杂度O(h)
3-7 找到二叉树中最大的拓扑结构
题目:给定一颗二叉树,已知所有节点的值都不一样, 返回其中最大的且符合搜索二叉树条件的最大拓扑结构的大小。拓扑结构是指树上的一个联通块。
题目意义解析:给定一颗二叉树,已知所有节点的值都不一样,找到树中最大的联通块,将其单独拿出来,要求满足(注意要把这个联通块单独拿出来看)
性质1:连通块内每一个节点需要满足大于左孩子节点小于右孩子节点,其中左右孩子节点都是联通块内的节点。
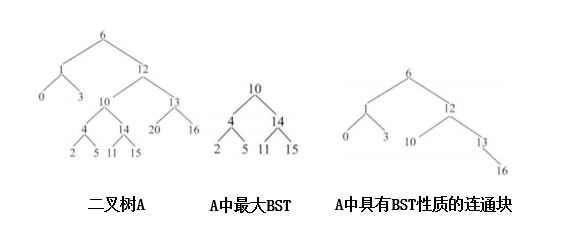
注意点:此题区别于上一题,这一题所求的联通块未必是二叉树的子树。是二叉树的一部分。
基本思想:
step1: 将求树中满足性质的最大联通块数目? ===> 子问题:求以s节点为根节点的最大联通块数目? 原问题就转换为求解n个子问题,取最大值?(n是二叉树节点数目)。
step2: 将求以s节点为根节点树的最大联通块数目? ===> 核心问题:求解s节点与t节点是否满足性质1(s是t的父节点)? 然后通过遍历以s为根节点的树,每遍历到一个节点就判断一次,符合要求就加上1。
题目难点:问题进行拆解的思维要有。
代码(时间复杂度为O(N^2))
#include <bits/stdc++.h>
using namespace std;
#define MAXN 200001
vector<int> nodes[MAXN];
/*判断树中节点s到节点t的路径是否为满足要求的联通块*/
/* 节点s时节点t的父节点*/
bool isBlock(int s,int t){
if(s == 0 || t == 0)
return false;
if(s == t)
return true;
if(s > t) // 往左遍历
return isBlock(nodes[s][0],t);
else // 往右遍历
return isBlock(nodes[s][1],t);
}
// 以s为根节点进行搜索,计算满足要求的节点数目。
void getMaxBlock(int s,int t,int &amount){
if(s == 0 || t == 0)
return;
// 判断节点t能否加入以s为根节点的联通块
if(isBlock(s,t)){
amount += 1;
getMaxBlock(s,nodes[t][0],amount);
getMaxBlock(s,nodes[t][1],amount);
}
}
/*对树中每个节点,求以它为根节点的满足要求的最大联通块数目,保留最大值*/
void preorder(int cur,int &max_num){
if(cur == 0)
return;
int amount = 0;
// 求以cur为根节点的最大联通块节点数
getMaxBlock(cur, cur,amount);
max_num = max(amount,max_num);
preorder(nodes[cur][0],max_num);
preorder(nodes[cur][1],max_num);
}
int main(){
int n,root;
scanf("%d %d",&n,&root);
int fa,lch,rch;
for(int i = 0;i < n;++i){
scanf("%d %d %d",&fa,&lch,&rch);
nodes[fa].push_back(lch);
nodes[fa].push_back(rch);
// printf("%d %d %d\n",fa,lch,rch);
}
int max_num = 0;
preorder(root,max_num);
printf("%d\n",max_num);
}
此题代码面试指南中有一个O(nlogn),有空再研究吧。
3-8 二叉树的按层打印以及ZigZag打印
题意:
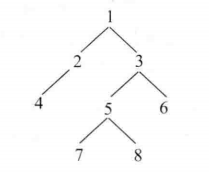
输入:
8 1
1 2 3
2 4 0
4 0 0
3 5 6
5 7 8
6 0 0
7 0 0
8 0 0
输出:
Level 1 : 1
Level 2 : 2 3
Level 3 : 4 5 6
Level 4 : 7 8
Level 1 from left to right: 1
Level 2 from right to left: 3 2
Level 3 from left to right: 4 5 6
Level 4 from right to left: 8 7
按层打印基本思想:
- 采用队列确定节点总体的顺序
- 采用2个变量来确定打印换行符的时机,当left_num=0打印换行符,并令left_num=acc_num,acc_num=0.
- left_num:当前层未打印的节点个数(出队时递减这个数字)
- acc_num:用于累加下一层节点的数目(入队时递增这个数字)
ZigZag打印的基本思想:
-
采用双端队列替换之前的单向队列,总体框架依旧延续按层打印的思想
当需要逆序打印的时候
- 队尾出列打印值
- 子节点从队头插入时,顺序应是先右后左。
当需要顺序打印的时候:
- 队头出列打印值
- 子节点从队尾插入时,顺序应是先左后右。
ZigZag打印代码
import java.util.*;
/*
* public class TreeNode {
* int val = 0;
* TreeNode left = null;
* TreeNode right = null;
* }
*/
public class Solution {
/**
*
* @param root TreeNode类
* @return int整型ArrayList<ArrayList<>>
*/
public ArrayList<ArrayList<Integer>> zigzagLevelOrder (TreeNode root) {
ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
LinkedList<TreeNode> deq = new LinkedList<TreeNode>();
if(root == null)
return res;
deq.addLast(root);
int node_num = 1;
int deep = 0;
int ans = 0;
boolean reverse = false;
while(deq.size() != 0){
if(res.size() < deep+1)
res.add(new ArrayList<Integer>());
if(!reverse){
TreeNode tmp = deq.removeFirst();
--node_num;
res.get(deep).add(tmp.val);
if(tmp.left != null){
deq.addLast(tmp.left);
++ans;
}
if(tmp.right != null){
deq.addLast(tmp.right);
++ans;
}
}else{
TreeNode tmp = deq.removeLast();
--node_num;
res.get(deep).add(tmp.val);
if(tmp.right != null){
deq.addFirst(tmp.right);
++ans;
}
if(tmp.left != null){
deq.addFirst(tmp.left);
++ans;
}
}
if(node_num == 0){
++deep;
node_num = ans;
ans = 0;
reverse = !reverse;
}
}
return res;
}
}
3-9 调整搜索二叉树中的二个错误节点
题目:一棵二叉树原本是搜索二叉树,但是其中有两个节点调换了位置,使得这棵二叉树不再是搜索二叉树,请按升序输出这两个错误节点的值。(每个节点的值各不相同)
基本思想:采用中序遍历(正确的BST应该是一个升序序列)
- 第一个错误节点是第一次降序时较大的节点
- 第二个错误节点是最后一次降序时较小的节点(可能只会出现一次降序,当2个节点是相邻节点)。
时间复杂度:O(N) 空间复杂度:O(1)
3-10 判断t1是否存在与t2相同的拓扑结构
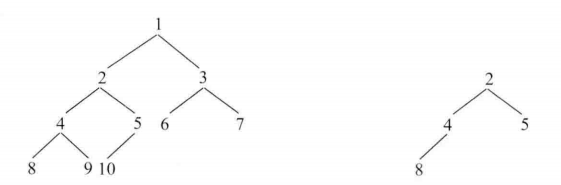
注意点:注意是拓扑结构,而非子树
基本思想:
step1:设计递归函数,给定树中一个节点m与t2(判断是否存在以m为根节点的拓扑结构与t2相同,这里要以按照t2的结构对2棵树同步比较!!!)
- t2遍历方便条件的判定
step2:遍历t1,每遇到一个节点都调用步骤1的bool函数判断该节点是否与t2结构相同。
时间复杂度 O(N*M) ,N与M分别是2棵树的节点个数。
3-11 判断t1是否存在与t2相同的子树
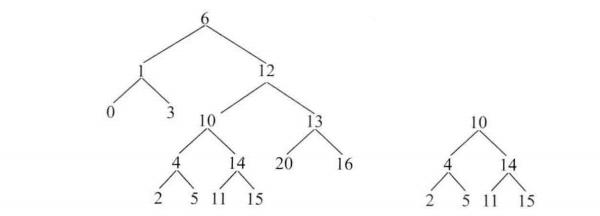
注意:区分子树与拓扑结构,其微妙程度类似于题目3-7和3-6(下图中给出了2个例子)
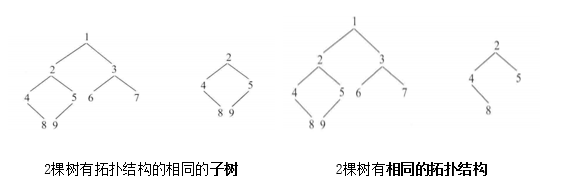
方法1:利用与3-10相似的解法
step1:设计递归函数,给定2个根节点,判断2棵树是否相同(按照t1的结构对2棵树同步比较!!!)
- 如果按照t2结构同步比较,t1被遍历的部分未必是一颗子树,因此必须对t1的子树遍历完整。
- 注意要返回t1遍历的子树的节点个数,避免只是相似的局部子结构
step2:遍历t1,每遇到一个节点都调用步骤1的bool函数判断该节点是否与t2结构相同,此外确保t1的子树的节点个数等于t2的节点个数。
- 优化点:可以提前计算节点的个数,选择满足条件的子树。
时间复杂度 O(N*M) ,N与M分别是2棵树的节点个数。
#include<iostream>
#include<vector>
#define MAXN 500001
using namespace std;
//对比T1的每个子树与T2,并且保证遍历完子树的节点数等于t2的节点数,防止只是相似的局部子结构
vector<int> T1[MAXN];
vector<int> T2[MAXN];
bool have = false;
// 通过引用获取子树遍历节点数以及比较结果
void isSameTree(int cur1,int cur2,int &count,bool &res){
if(cur1 == 0)
return;
if(cur1 != cur2){
res = false;
return;
}
++count;
isSameTree(T1[cur1][0],T2[cur2][0],count,res);
if(!res)
return;
isSameTree(T1[cur1][1],T2[cur2][1],count,res);
}
void preorder(int cur,int root2,int num2){
if(cur == 0)
return;
int count = 0;
bool res = true;
isSameTree(cur,root2,count,res);
if(res && num2 == count)
have = true;
if(have)
return;
preorder(T1[cur][0],root2,num2);
if(have)
return;
preorder(T1[cur][1],root2,num2);
}
int main()
{
int n1,root1;
cin >> n1 >> root1;
int fa,lch,rch;
for(int i = 0;i < n1;++i){
cin >> fa >> lch >> rch;
T1[fa].push_back(lch);
T1[fa].push_back(rch);
}
int n2,root2;
cin >> n2 >> root2;
for(int i = 0;i < n2;++i){
cin >> fa >> lch >> rch;
T2[fa].push_back(lch);
T2[fa].push_back(rch);
}
int count = 0;
bool res = true;
preorder(root1,root2,n2);
if(have)
cout << "true" << endl;
else{
cout << "false" << endl;
}
return 0;
}
方法2:利用KMP算法
step1:将2棵树都转化为唯一的字符串表示。
step2:利用KMP算法判断s1中是否包含s2。
3-12 判断二叉树是否为平衡二叉树
基本思想:后序遍历树并设计递归函数返回以当前节点为根节点的树的最大深度
- 注意:1个节点代表这颗树深度为1,遇到空指针返回0
#include<bits/stdc++.h>
using namespace std;
#define MAXN 500001
vector<int> nodes[MAXN];
/*返回以cur节点为头节点的树的最大深度*/
int preorder(int cur, int deep, bool &res){
if(cur == 0)
return 0;
int leftMax = preorder(nodes[cur][0],deep+1,res);
int rightMax = preorder(nodes[cur][1],deep+1,res);
int dis = leftMax-rightMax;
if(dis > 1 || dis <-1)
res = false;
return 1+max(leftMax,rightMax);
}
int main(){
int n,root;
scanf("%d %d",&n,&root);
int fa,lch,rch;
for(int i = 0;i < n;++i){
scanf("%d %d %d",&fa,&lch,&rch);
nodes[fa].push_back(lch);
nodes[fa].push_back(rch);
// printf("%d %d %d\n",fa,lch,rch);
}
bool res = true;
preorder(root,1,res);
if(res)
printf("true");
else
printf("false");
}
3-13 根据后序数组重建搜索二叉树
题意:给定一个有 n 个不重复整数的数组 arr,判断 arr 是否可能是节点值类型为整数的搜索二叉树后序遍历的结果。
基本思想:递归思想 + 后序遍历序列 = 左子树 右子树 根节点
输入:序列数组的首尾索引
输出: 子数组是否是后序遍历序列。
注意点:保证右子树的节点 > 左子树节点
#include<bits/stdc++.h>
using namespace std;
vector<int> arr;
/*s与e分别是头尾索引*/
bool isPost(int s,int e){
if(s == e)
return true;
int i;
for(i = s;i < e;++i){
if(arr[i] > arr[e])
break;
}
// 只有右子树或者左子树
if(i == s || i == e)
return isPost(s,e-1);
// 确保右子树序列都大于根节点
for(int j = i;j < e;++j){
if(arr[j] < arr[e])
return false;
}
return isPost(i,e-1) && isPost(s,i-1);
}
int main(){
int n;
scanf("%d",&n);
int tmp;
for(int i = 0;i < n;++i){
scanf("%d",&tmp);
arr.push_back(tmp);
}
// printf("%d",arr.size());
bool res = isPost(0,arr.size()-1);
if(res)
printf("true\n");
else
printf("false\n");
}
总结:
- 数组只进行访问,做题时候切忌不要传递数组
- 可以作为公共变量
- 也可以作为引用传递
3-14 二叉树2个节点的最近公共祖先(LCA问题)
题0:找到二叉搜索树的最近公共父节点?(递归法)
基本思想:递归法,根据当前节点与2个目标节点的值返回恰当的节点指针。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == NULL)
return NULL;
int val = root->val;
if(p->val < val && q->val < val)
return lowestCommonAncestor(root->left, p, q);
else if(p->val > val && q->val > val)
return lowestCommonAncestor(root->right, p, q);
else
return root;
}
};
题1:给定一棵二叉树以及这棵树上的两个节点 o1 和 o2,请找到 o1 和 o2 的最近公共祖先节点(递归法)。
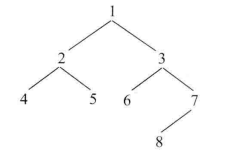
上图中节点4,5公共节点是2,节点5和2最近公共节点是7。
题1基本思想:递归法
时间复杂度: O(n)
#include<bits/stdc++.h>
using namespace std;
#define MAXN 500002
vector<int> nodes[MAXN];
int lowestAncestor(int cur,int t1,int t2){
if(cur == 0 || cur == t1 || cur == t2)
return cur;
int left = lowestAncestor(nodes[cur][0],t1,t2);
int right = lowestAncestor(nodes[cur][1],t1,t2);
if(left != 0 && right != 0)
return cur;
else if(left != 0)
return left;
else if(right != 0)
return right;
else
return 0;
}
int main(){
int n,root;
cin >> n >> root;
int fa,lch,rch;
for(int j = 0;j < n;++j){
cin >> fa >> lch >> rch;
nodes[fa].push_back(lch);
nodes[fa].push_back(rch);
}
int t1,t2;
cin >> t1 >> t2;
cout << lowestAncestor(root,t1,t2) << endl;
return 0;
}
题2 批量返回公共父节点。
代码面试指南提供两个解法:
方法1:利用hash表或者存储每个节点的父节点指针,或者重新构造树带有父节点和节点深度的指针。
时间复杂度:O(n)+ O(h) *查询次数
#include<bits/stdc++.h>
using namespace std;
struct Node{
int lc = 0;
int rc = 0;
int parent = -1;
int level;
};
// 确定每个结点所在层
void getNodeLevel(vector<Node>& tree,int root)
{
if(!root) return;
// 左子树各节点的level
if(tree[root].lc)
{
tree[tree[root].lc].level = tree[root].level + 1;
getNodeLevel(tree,tree[root].lc);
}
// 右子树各节点的level
if(tree[root].rc)
{
tree[tree[root].rc].level = tree[root].level + 1;
getNodeLevel(tree,tree[root].rc);
}
// 设置根节点的level
if(tree[root].parent == -1)
return;
tree[root].level = tree[tree[root].parent].level + 1;
}
int LCA(vector<Node>& tree,int o1,int o2)
{
// 把层次深的节点一直沿父节点上移 直到两个节点处于同一level
// 同一层次的节点同时沿各自的父节点上移,第一个相遇的节点就是LCA
while(o1 != o2)
{
if(tree[o1].level>tree[o2].level)
o1 = tree[o1].parent;
else if(tree[o1].level<tree[o2].level)
o2 = tree[o2].parent;
else
{
o1 = tree[o1].parent;
o2 = tree[o2].parent;
}
}
return o1;
}
int main()
{
int n,root;
cin>>n>>root;
vector<Node>tree(n+1);
int pa,l,r;
for(int i=0;i<n;++i)
{
cin>>pa;
cin>>l>>r;
tree[pa].lc = l;
tree[pa].rc = r;
if(l) tree[l].parent = pa;
if(r) tree[r].parent = pa;
}
getNodeLevel(tree,root);
int m;
int o1,o2;
cin>>m;
while(m--)
{
cin>>o1>>o2;
cout<<LCA(tree,o1,o2)<<endl;
}
}
题3:O(n+m)的时间复杂度返回批量查询的公共父节点。(带学习)
方法1: 并查集加+tarjan离线算法
3-15 二叉树节点之间的最大距离问题
基本思想:递归法
以当前节点为根节点的树的最大距离有三种情况:
情况1:左子树最大距离
情况2:右子树最大距离
情况3:左右子树最大深度的和+1(左右子树的高度和+1)
代码的实现利用深度计算(繁杂版):
- 自己实现的时候比较繁琐,主要在于树的高度计算通过深度差进行计算
#include<bits/stdc++.h>
using namespace std;
#define MAXN 500002
vector<int> nodes[MAXN];
struct Res{
int maxDis;
int maxDeep;
};
/*每个递归函数需要获取左右子树的最大深度以及最大距离,
并返回以当前节点为根节点的最大深度与最大距离。
*/
Res maxDistance(int cur,int deep){
Res res;
if(cur == 0){
res.maxDis = 0;
res.maxDeep = deep-1;
return res;
}
Res lres = maxDistance(nodes[cur][0],deep+1);
Res rres = maxDistance(nodes[cur][1],deep+1);
// 左子树高度+右子树高度+1
int tmp = (lres.maxDeep-deep)+(rres.maxDeep-deep)+1;
res.maxDis = max(tmp,max(lres.maxDis,rres.maxDis));
res.maxDeep = max(lres.maxDeep,rres.maxDeep);
return res;
}
int main(){
int n,root;
cin >> n >> root;
int fa,lch,rch;
for(int j = 0;j < n;++j){
cin >> fa >> lch >> rch;
nodes[fa].push_back(lch);
nodes[fa].push_back(rch);
}
Res res = maxDistance(root,1);
cout << res.maxDis << endl;
return 0;
}
代码实现(利用深度计算简洁版本)
#include<bits/stdc++.h>
using namespace std;
#define MAXN 500002
vector<int> nodes[MAXN];
int maxDistance(int cur,int deep,int &maxd){
if(cur == 0){
maxd = deep-1;
return 0;
}
int lmax = maxDistance(nodes[cur][0],deep+1,maxd);
int ld = maxd;
int rmax = maxDistance(nodes[cur][1],deep+1,maxd);
int rd = maxd;
// 左子树高度+右子树高度+1
int tmp = (ld-deep)+(rd-deep)+1;
maxd = max(ld,rd);
return max(tmp,max(lmax,rmax));;
}
int main(){
int n,root;
cin >> n >> root;
int fa,lch,rch;
for(int j = 0;j < n;++j){
cin >> fa >> lch >> rch;
nodes[fa].push_back(lch);
nodes[fa].push_back(rch);
}
int maxd;
cout << maxDistance(root,1,maxd);
return 0;
}
关于递归中引用的变量的思考:
引用的变量在递归过程中主要用于实时的记录当前某个变量的状态。递归过程中常用于2个场景:
1.需要考虑全局的结果,比如说3-12,3-7(本质上是搜索题,这时采用全局变量也是ok的)
2.用于实时记录每个子问题的结果并在递归过程中实时的使用,注意这类子问题的求解都是具有递归性的,比如3-15以及3-6结构体虽然是返回值但也完全可以作为引用传递。
代码实现(利用高度计算)
#include<bits/stdc++.h>
using namespace std;
#define MAXN 500002
vector<int> nodes[MAXN];
int maxDistance(int cur,int &h){
if(cur == 0){
h = 0;
return 0;
}
int lmax = maxDistance(nodes[cur][0],h);
int lh = h;
int rmax = maxDistance(nodes[cur][1],h);
int rh = h;
// 左子树高度+右子树高度+1
int tmp = (lh)+(rh)+1;
h = 1+ max(lh,rh);
return max(tmp,max(lmax,rmax));;
}
int main(){
int n,root;
cin >> n >> root;
int fa,lch,rch;
for(int j = 0;j < n;++j){
cin >> fa >> lch >> rch;
nodes[fa].push_back(lch);
nodes[fa].push_back(rch);
}
int h = 0;
cout << maxDistance(root,h);
return 0;
}
关于树的高度与深度的个人体会:
- 树的高度从叶节点开始累计,如果是叶节点直接返回0
- 树的深度需要从节点开始累计,如果递归到叶节点直接deep-1
- 解题时能用高度替代深度,少用一个变量去记录当前的深度。但也有例外,比如问题3-5。
3-17 2种遍历序列构造树的的系列问题
01 先序+中序推出后序
基本思想(递归实现)
- 每一次递归待用处理一个节点,利用前序的第一个节点是根节点,然后找到中序遍历的根节点索引,确定左右子树序列的长度。
- 索引查找如有必要可以通过hash表提高查找效率。
| 根节点 | 左子树 | 右子树 | |
|---|---|---|---|
| 前序遍历序列 | 1 | 2,4,5,8,9 | 3,6,7 |
| 左子树 | 根节点 | 右子树 | |
| 中序遍历序列 | 4,2,8,5,9 | 1 | 6,3,7 |
代码实现(时间复杂度O(n^2))
#include<bits/stdc++.h>
using namespace std;
vector<int> pre;
vector<int> in;
bool first = true;
struct Node{
int v;
Node* l;
Node* r;
};
Node* buildTree(int s1,int e1,int s2,int e2){
if(s1 > e1 || s2 > e2)
return NULL;
Node* root = new Node();
root->v = pre[s1];
int tmp;
for(int j = s2;j <= e2;++j){
if(in[j] == root->v)
tmp = j;
}
int left_len = tmp - s2;
root->l = buildTree(s1+1,s1+left_len,s2,tmp-1);
root->r = buildTree(s1+left_len+1,e1,tmp+1,e2);
return root;
}
void postorder(Node* root){
if(root == NULL)
return;
postorder(root->l);
postorder(root->r);
if(first){
printf("%d",root->v);
first = false;
}
else
printf(" %d",root->v);
}
int main(){
int n;
cin >> n;
int tmp;
for(int i = 0;i < n;++i){
cin >> tmp;
pre.push_back(tmp);
}
for(int i = 0;i < n;++i){
cin >> tmp;
in.push_back(tmp);
}
Node* root = buildTree(0,n-1,0,n-1);
postorder(root);
return 0;
}
基本思想:递归的方法,基本思想同上。
- 根据后序序列的最后一个节点是根节点,然后在中序中获得根节点索引从而确定左右子树长度。
| 左子树 | 根节点 | 右子树 | |
|---|---|---|---|
| 中序遍历序列 | 9 | 3 | 15,20,7 |
| 左子树 | 右子树 | 根节点 | |
| 后序遍历序列 | 9 | 15,7,20 | 3 |
代码实现:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
unordered_map<int,int> mymap;
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
for(int i = 0;i < inorder.size();++i)
mymap[inorder[i]] = i;
int size = inorder.size()-1;
return build(0,size,0,size,inorder,postorder);
}
TreeNode* build(int s1,int e1,int s2,int e2,vector<int>& inorder, vector<int>& postorder){
if(s1 > e1 || s2 > e2)
return NULL;
TreeNode* root = new TreeNode();
root->val = postorder[e2];
int index = mymap[root->val];
int leftlen = index-s1;
root->left = build(s1,index-1,s2,s2+leftlen-1,inorder, postorder);
root->right = build(index+1,e1,s2+leftlen,e2-1,inorder, postorder);
return root;
}
};
3-18 统计和生成所有的二叉树
题意:给出一个整数 n,如果 n < 1,代表空树,否则代表中序遍历的结果为 {1, 2, 3... n}。请输出可能的二叉树结构有多少。
注意:题目中显然是一棵BST。
基本思想:动态规划
定义问题 : dp[i] 表示 i 个节点的BST的子结构数目 =
编号为1的节点作为根节点的子结构数目 + 编号为2的节点作为根节点的子结构数目 + 编号为3的节点作为根节点的子结构数目 + .... 编号为i的节点作为根节点的子结构数目
编号为k的节点作为根节点的子结构数目 = dp[k-1]*dp[i-k] = k-1个节点的BST子结构 * i-k个节点的BST子结构
- 左子树有k-1个节点 dp[k-1]
- 右子树有i-k个节点dp[i-k]
#include <bits/stdc++.h>
using namespace std;
#define N 10001
#define MOD 1000000007
int main(){
vector<long> dp(N,0);
int n;
int mod = 1e9+7;
cin >> n;
dp[0] = 1;
dp[1] = 1;
for(int i = 2;i <= n;++i){ // 枚举BST中包含节点个数
for(int j = 1; j <= i;++j){ // 枚举以哪个节点作为根节点
dp[i] += dp[j-1] * dp[i-j]; // 左子树*右子树(累加所有可能性)
dp[i] %= mod;
}
}
cout << dp[n] << endl;
return 0;
}
3-19 派对最大的欢乐值
补充题目
二叉树中的最大路径和
用到的数据结构方法
动态数组vector
vector<int> my_vector;
[] // 访问与修改数据
my_vector.push_back(v); // 从尾端插入数据
key不重复的hashmap表的使用
unordered_map<int,int> treemap;
treemap[key] = value; // 插入与修改数据
if(treemap.find(cur_sum) != treemap.end()) // 判断hashmap是否包含key
treemap.erase(cur_sum) // 根据key删除每条记录
思考
设计递归函数的时候,参数通过引用传递好,还是通过返回值传递好?
- 实际上通过返回值传递的一定可以通过引用传递,那种方式符合思维习惯,使用哪一种。
- 采用返回值传递时必须保证子问题的求解只与其分解的子问题相关。
树的基本代码
树的定义
采用离散的物理存储地址
--第一种方式定义
struct Node{
int value;
Node* left;
Node* rigth;
}
typedef struct Node* PtrNode;
采用连续的物理存储地址(使用数组的下标作为指针):实际刷题比较方便
const int maxn = 1000;
struct node{
int data;
vector<int> child;
} Node[maxn];
/*如果树的节点没有数据域,那们可定义如下*/
vector<int> child[maxn];
- 好处:有利于根据树的节点值快速访问该节点
树的创建
输入数据格式
---------------------------------------------------------------------------------------
输入描述:第一行输入两个整数 n 和 root,n 表示二叉树的总节点个数,root 表示二叉树的根节点。以下 n 行每行三个整数 fa,lch,rch,表示 fa 的左儿子为 lch,右儿子为 rch。(如果lch为0则表示fa没有左儿子,rch同理)
---------------------------------------------------------------------------------------
8 1
1 2 3
2 4 5
4 0 0
5 0 0
3 6 7
6 0 0
7 8 0
8 0 0
采用离散的物理存储地址
- 这种方法建树对数据的输入次序要求非常严格,写也不是很方便,没有必要的话不用这种方式。
- 除非题目中对数据的输入格式进行了明确的说明,牛客网相关题目就缺少说明。
比如下面的输入数据不适合递归的方法建树。
- 11行数据与12和13行数据无法递归建树,该输入样例来源于
- 打印二叉树的边界节点
16 1
1 2 3
2 0 4
4 7 8
7 0 0
8 0 11
11 13 14
13 0 0
14 0 0
3 5 6
5 9 10 // 11行数据与12和13行数据无法递归建树
10 0 0
9 12 0
12 15 16
15 0 0
16 0 0
6 0 0
struct TreeNode{
int val;
TreeNode* lch;
TreeNode* rch;
TreeNode(int x):val(x),lch(NULL),rch(NULL){}
};
// 方法1:采用递归的方式建立树,这种方式是基于对输入数据的观察,先左子树后右子树
void createTree(TreeNode* root, int& cnt){
if(cnt == 0) return;
int p, l, r;
cin >> p >> l >> r;
if(l){
TreeNode* lch = new TreeNode(l);
root->lch = lch;
createTree(root->lch, --cnt);
}
if(r){
TreeNode* rch = new TreeNode(r);
root->rch = rch;
createTree(root->rch, --cnt);
}
return;
}
//方法1的另外一种写法:采用递归的方式建树
void buildTree(Node* &root,int value){
if(value == 0){
root = NULL;
return;
}
int fa,lch,rch;
cin >> fa >> lch >> rch;
root = new Node();
root->v = value;
buildTree(root->left,lch);
buildTree(root->right,rch);
}
采用连续的物理存储地址(使用数组的下标作为指针)
- 要求节点必须是int类型变量并且每个节点值是唯一的,写法上比较方便。
vector<int> nodes[MAXN];
void createTree(){
int n,root;
scanf("%d %d",&n,&root);
int fa,lch,rch;
for(int i = 0;i < n;++i){
scanf("%d %d %d",&fa,&lch,&rch);
nodes[fa].push_back(lch);
nodes[fa].push_back(rch);
// printf("%d %d %d\n",fa,lch,rch);
}

 《程序员面试指南》第三章相关的知识点,方便回顾
《程序员面试指南》第三章相关的知识点,方便回顾

 浙公网安备 33010602011771号
浙公网安备 33010602011771号