python 解积分方程

引用:https://www.aliyun.com/jiaocheng/527786.html

sympy求解极限、积分、微分、二元一次方程：http://www.gzhshoulu.wang/article/3761158

https://docs.scipy.org/doc/scipy/reference/tutorial/integrate.html

解方程组  2*x-y=3，3*x+y=7

from sympy import *
x=Symbol('x') 
y=Symbol('y') 
print solve([2*x-y-3,3*x+y-7],[x,y])
# result is: {x: 2, y: 1}

求积分  ((n+3)/(n+2))**n，limit n->oo

from sympy import *
n=Symbol('n') 
s=((n+3)/(n+2))**n 
print limit(s,n,oo)
# result is: E

　 

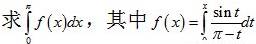
from sympy import *
t=Symbol('t') 
x=Symbol('x') 
m=integrate(sin(t)/(pi-t),(t,0,x)) 
n=integrate(m,(x,0,pi)) 
print m
# result is: Si(x - pi) + Si(pi)
print n
# result is: 2

sympy求导1

import numpy as np
from sympy.abc import x

f = lambda x: x**3-2*x-6
# 我们设定参数h的默认值，如果调用函数时没有指明参数h的值，便会使用默认值
def derivative(f,h=0.00001):
    return lambda x: float(f(x+h)-f(x))/h
fprime = derivative(f)
print fprime(6)
# result is：106.000179994

sympy求导2

from sympy.abc import x

f = x**3-2*x-6
print f.diff()
# result is :3*x**2 - 2
print f.diff().evalf(subs={x:6})
# result is : 106.0000000000

sympy解方程

import sympy
from sympy.abc import x
f = x**2-2*x-4
print sympy.solve(f,x)
# result is：[1 + sqrt(5), -sqrt(5) + 1]

解方程 f''(x) - 2f'(x) + f(x) = sin(x) 

from sympy import *
init_printing()
# 给定符号
x = Symbol('x')
f, g = symbols('f g', cls=Function)
#solve f''(x) - 2f'(x) + f(x) = sin(x) 
diffeq = Eq(f(x).diff(x, x) - 2*f(x).diff(x) + f(x), sin(x))
#use dsolve,return Eq，hint control accuracy
print(dsolve(diffeq, f(x),))
#结果：Eq(f(x), (C1 + C2*x)*exp(x) + cos(x)/2)

　...