1_自动梯度

引言

pytorch的文档看过很多种，也看过许多autograd的文章，但总是有一种似懂非懂的感觉。但它又是pytorch较为核心的一个点，所以希望用一篇文章解决所有疑问！

基础

在深度学习中，我们经常需要对函数求梯度(gradient)。PyTorch提供的autograd包能够根据输入和前向传播过程自动构建计算图，并执行反向传播。一般的变量只会存储单个的值(数字、字符等)，但是tensor在操作时自动计算梯度并进行存储，我们可以通过autograd自带函数控制他这一行为。在讲解上述操作之前，我们需要了解一些基础概念：

张量(tensor)

张量在力学和数学中都有应用，但我们这里单纯地从深度学习的角度来看：

• Tensor实际上是一个多维数组，其目的是能够创造更高维度的矩阵、向量。
• 标量(0维张量)、矢量(1维张量)、矩阵(2维张量)、矩阵数组(3维张量)
• 更详细的解说可见：什么是张量？

计算图

从概念上讲，autograd在由函数对象组成的有向无环图（DAG）中保存数据（张量）和所有执行的操作（以及由此产生的新张量）的记录。在此 DAG 中，叶子是输入张量，根是输出张量。通过从根到叶跟踪此图，我们可以使用链式规则自动计算梯度。

在正向传递中，autograd同时执行两项操作：

• 运行请求的操作以计算生成的张量
• 在 DAG 中维护操作的梯度函数

在 DAG 根目录上调用后向传递时启动。 然后：.backward()（进行反向传播操作）

• 计算每个 的梯度，.grad_fn
• 将它们累加在各个张量的属性中，并且.grad
• 使用链规则，一直传播到叶张量。

下面是我们示例中 DAG 的可视化表示形式。在图表中，箭头位于正向传递的方向。节点表示正向传递中每个操作的向后函数。蓝色的叶节点表示我们的叶张量

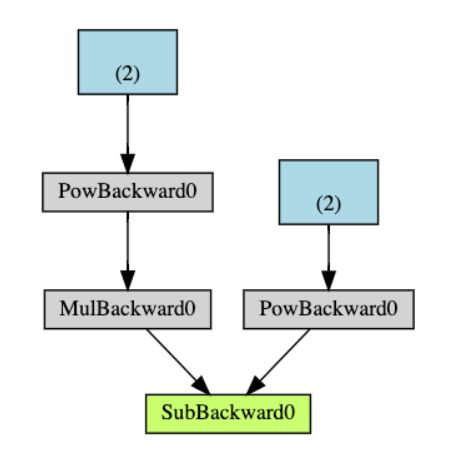
操作过程及相关函数

1. 如果将其属性.requires_grad设置为True，它将开始追踪(track)在其上的所有操作（这样就可以利用链式法则进行梯度传播了）。完成计算后，可以调用.backward()来完成所有梯度计算。此Tensor的梯度将累积到.grad属性中。

注意在y.backward()时，如果y是标量，则不需要为backward()传入任何参数；否则，需要传入一个与y同形的Tensor。

2. 如果不想要被继续追踪，可以调用.detach()将其从追踪记录中分离出来，这样就可以防止将来的计算被追踪，这样梯度就传不过去了。此外，还可以用with torch.no_grad()将不想被追踪的操作代码块包裹起来，这种方法在评估模型的时候很常用，因为在评估模型时，我们并不需要计算可训练参数（requires_grad=True）的梯度。

3. Function是另外一个很重要的类。Tensor和Function互相结合就可以构建一个记录有整个计算过程的有向无环图（DAG）。每个Tensor都有一个.grad_fn属性，该属性即创建该Tensor的Function, 就是说该Tensor是不是通过某些运算得到的，若是，则grad_fn返回一个与这些运算相关的对象，否则是None。

参考：官网-autograd

代码：可以查看代码文件夹下同名jupyter文件