DS博客作业04--图
|这个作业属于哪个班级|数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业04--图 |
| 这个作业的目标 |学习图结构设计及相关算法 |
| 姓名 | 陈佳桐 |
0.PTA得分截图

1.本周学习总结(6分)
1.1 图的存储结构
1.1.1 邻接矩阵
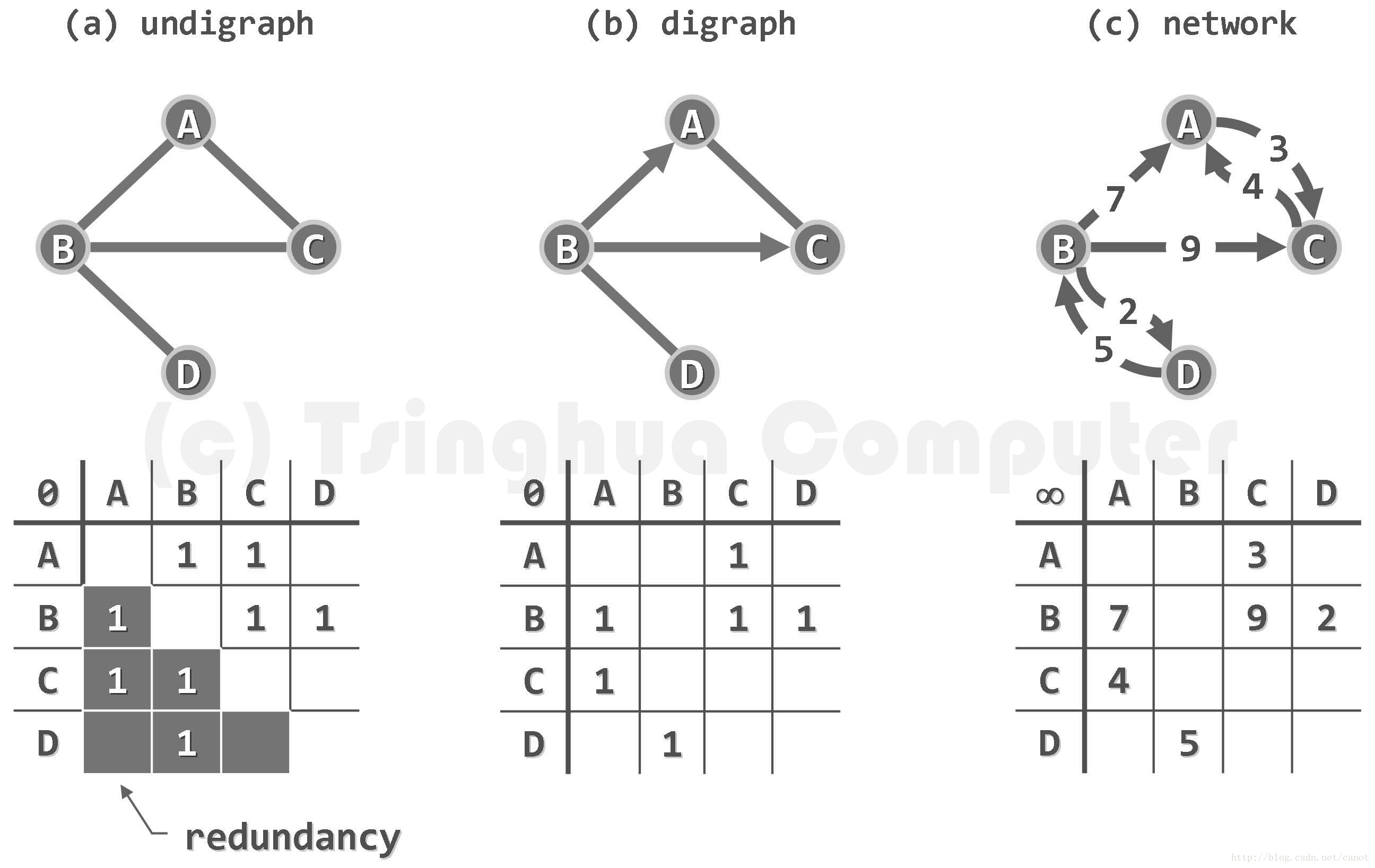
邻接矩阵的结构体定义
typedef struct
{ int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,弧数
} MGraph; //图的邻接矩阵表示类型
建图函数
void CreateMGraph(MGraph &g, int n, int e)//建图
{
//n顶点,e弧数
g.n = n;
g.e = e;
int i, j;
int a, b;//下标
for (i = 1; i <= n; i++)//先进行初始化
{
for (j = 1; j <= n; j++)
{
g.edges[i][j] = 0;
}
}
for (i = 1; i <= e; i++)//无向图
{
cin >> a >> b;
g.edges[a][b] = 1;
g.edges[b][a] = 1;
}
}
void CreateMGraph(MGraph& g, int n, int e)//建图
{
int i, j;
int a, b;
g.n = n; g.e = e; //
//建邻接矩阵
for (i = 0; i <= n; i++)
{
for (j = 0; j <= n; j++)
g.edges[i][j] = 0; //邻接矩阵初始化
}
for (i = 0; i < e; i++) //构建邻接矩阵
{
cin >> a >> b;
g.edges[a][b] = 1;
g.edges[b][a] = 1;
}
}
1.1.2 邻接表
邻接矩阵的结构体定义
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef struct
{ AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph; //邻接表类型
建图函数
void CreateAdj(AdjGraph*& G, int n, int e) //创建图邻接表
{
int i, j, a, b;
int A[MAXV][MAXV];
ArcNode* p;
G = (AdjGraph*)malloc(sizeof(AdjGraph));//申请动态储存
for (i = 0; i <= n; i++)//邻接表头指针指针置零
{
G->adjlist[i].firstarc = NULL;
}
for (i = 0; i < n; i++)//邻接矩阵初始化置零
{
for (j = 0; j <= n; j++)
{
A[i][j] = 0;
}
}
for (i = 0; i < e; i++)//邻接矩阵对应边置1
{
cin >> a >> b;
A[a][b] = 1; A[b][a] = 1;
}
//查找邻接矩阵中的每个元素
for (i = 1; i <= n; i++)
{
for (j = 1; j <= n; j++)
{
if (A[i][j])
{
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j; //存放临节点
p->info = A[i][j]; //放权值
p->nextarc = G->adjlist[i].firstarc; //头插法插入节点
G->adjlist[i].firstarc = p; //
}
}
}
G->n = n; G->e = e;
}
1.1.3 邻接矩阵和邻接表表示图的区别
适用情况:
邻接矩阵多用于稠密图的存储,而邻接表多用于稀疏图的存储。
区别:
①对于任一确定的无向图,邻接矩阵是唯一的(行列号与顶点编号一致),但邻接表不唯一(链接次序与顶点编号无关)。
②邻接矩阵的空间复杂度为o(n2),而邻接表的空间复杂度为o(n+e)。
1.2 图遍历
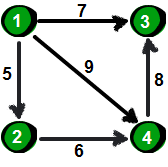
1.2.1 深度优先遍历
选上述的图,继续介绍深度优先遍历结果
深度遍历代码:
DFS方法首先从根节点1开始,其搜索节点顺序是1,2,3,4,5,6,7,8(假定左分枝和右分枝中优先选择左分枝)。
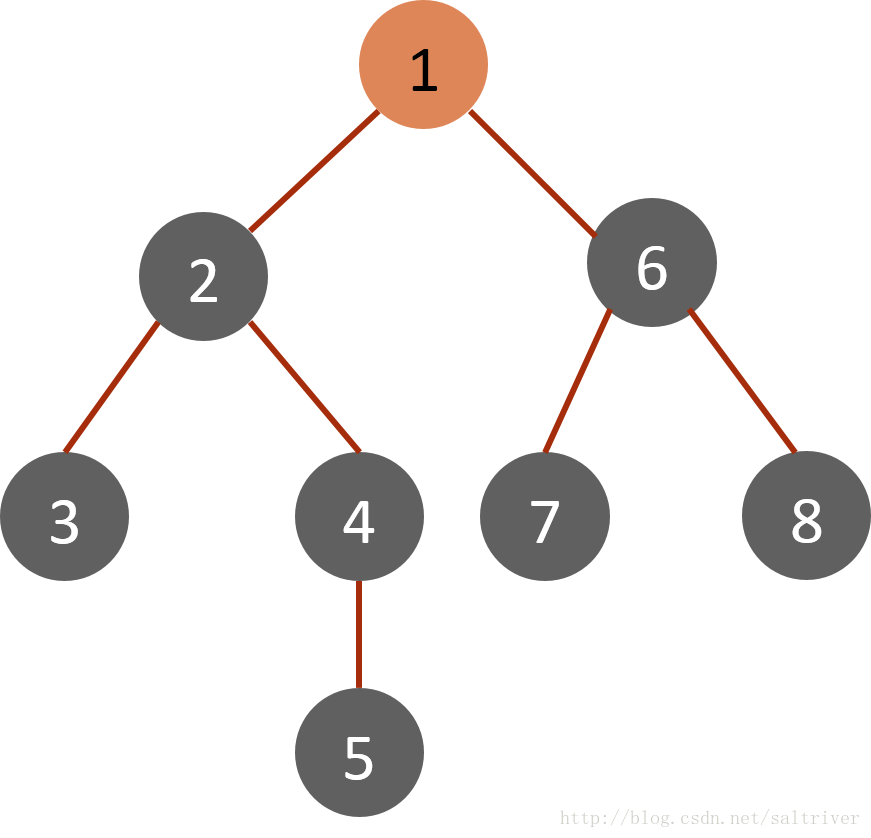
(1)将起始节点1放入栈stack中,标记为已遍历。

(2)从stack中访问栈顶的节点1,找出与节点1邻接的节点,有2,9两个节点,我们可以选择其中任何一个,选择规则可以人为设定,这里假设按照节点数字顺序由小到大选择,选中的是2,标记为已遍历,然后放入stack中。

(3)从stack中取出栈顶的节点2,找出与节点2邻接的节点,有1,3,5三个节点,节点1已遍历过,排除;3,5中按照预定的规则选中的是3,标记为已遍历,然后放入stack中。
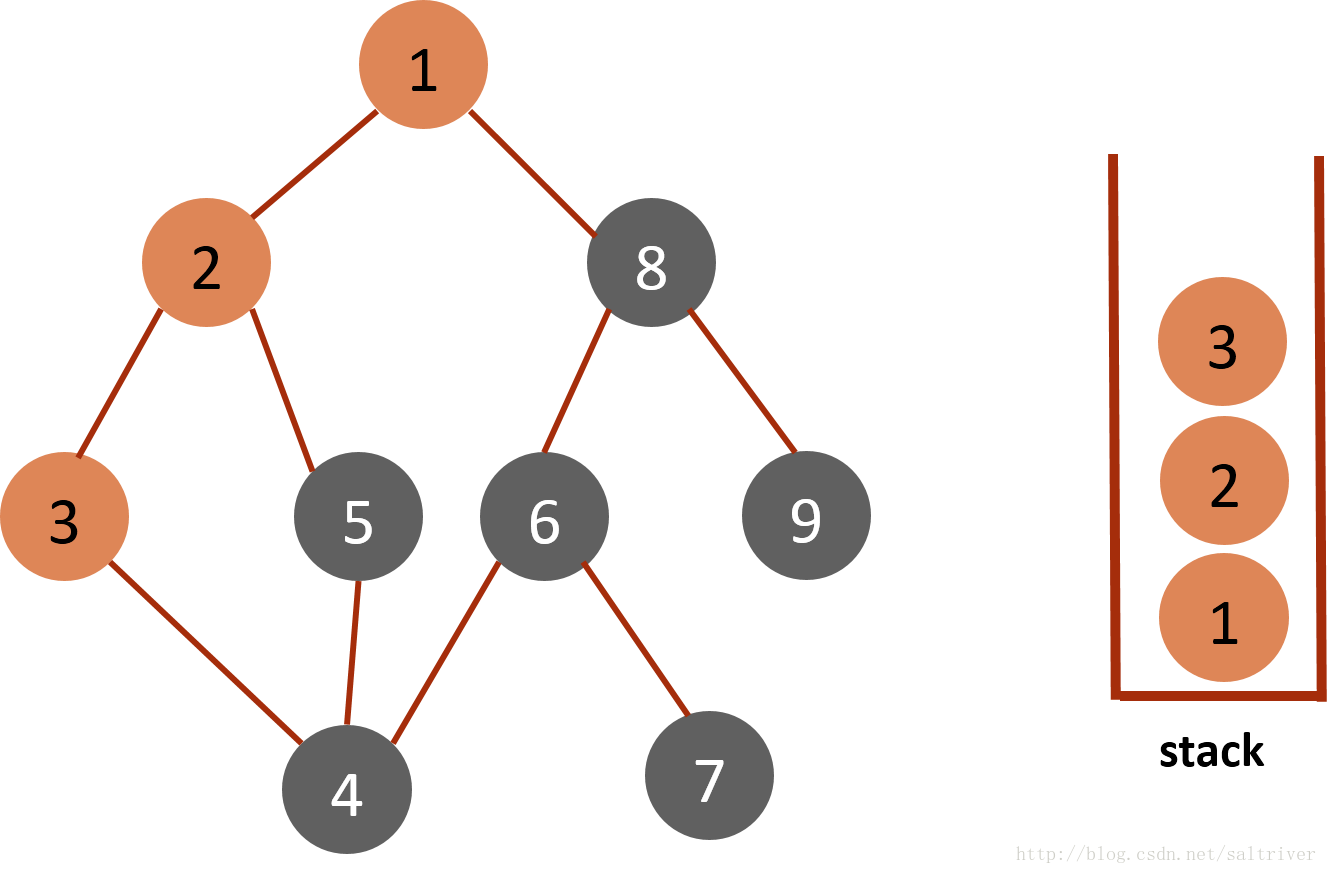
(4)从stack中取出栈顶的节点3,找出与节点3邻接的节点,有2,4两个节点,节点2已遍历过,排除;选中的是节点4,标记为已遍历,然后放入stack中。
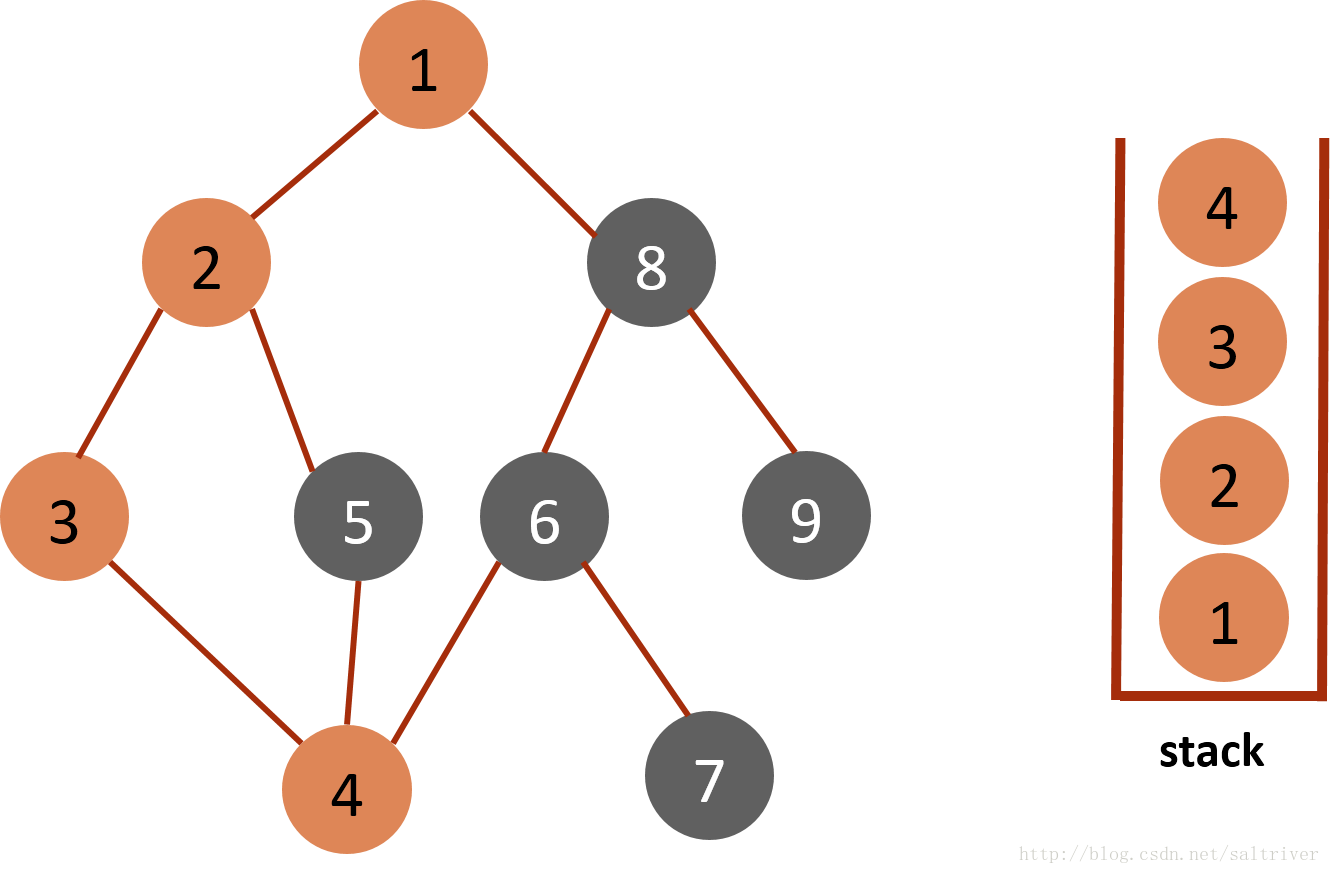
(5)从stack中取出栈顶的节点4,找出与节点4邻接的节点,有3,5,6三个节点,节点3已遍历过,排除;选中的是节点5,标记为已遍历,然后放入stack中。
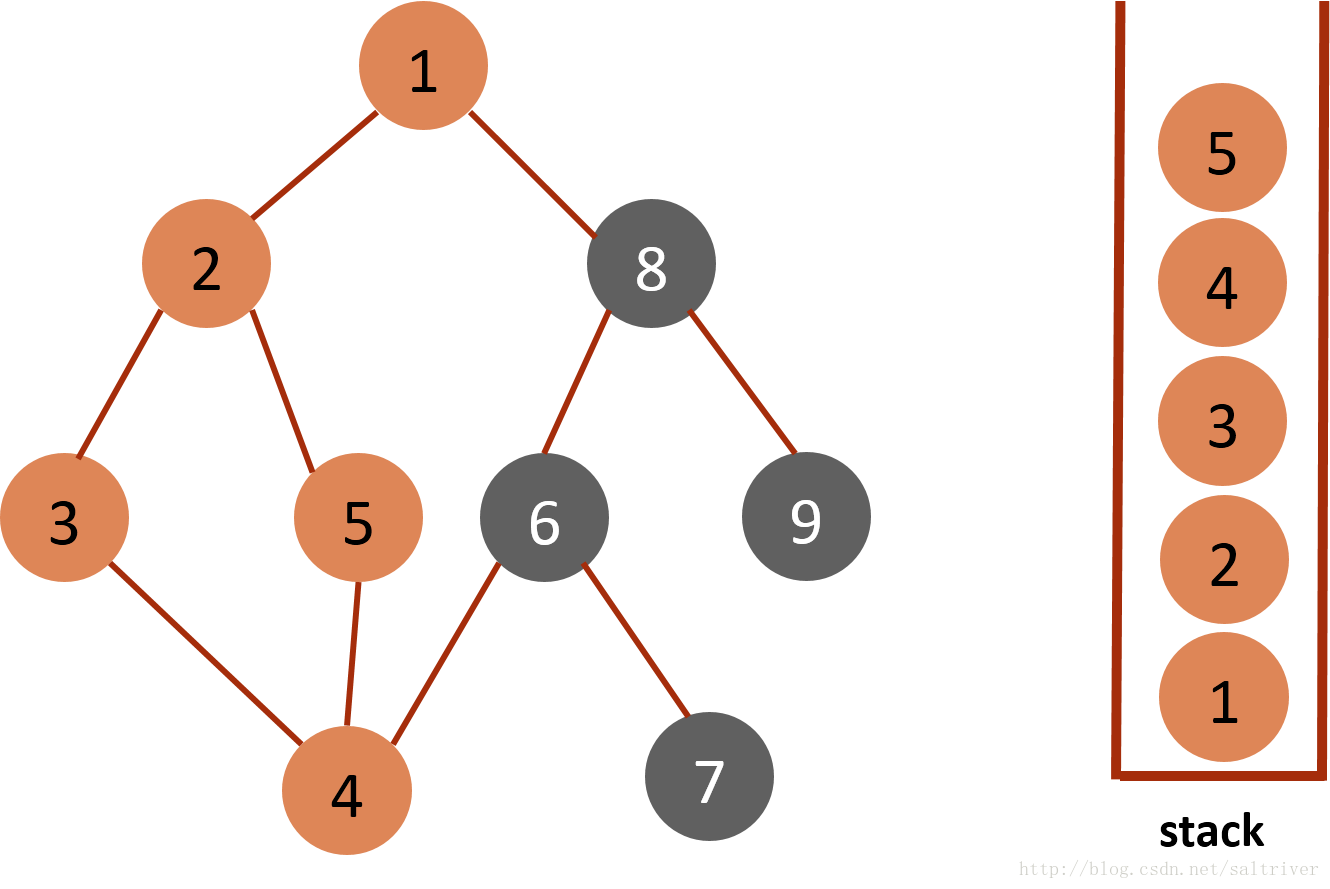
(6)从stack中取出栈顶的节点5,找出与节点5邻接的节点,有2,4两个节点,节点2,4都已遍历过,因此节点5没有尚未遍历的邻接点,则将此点从stack中弹出。
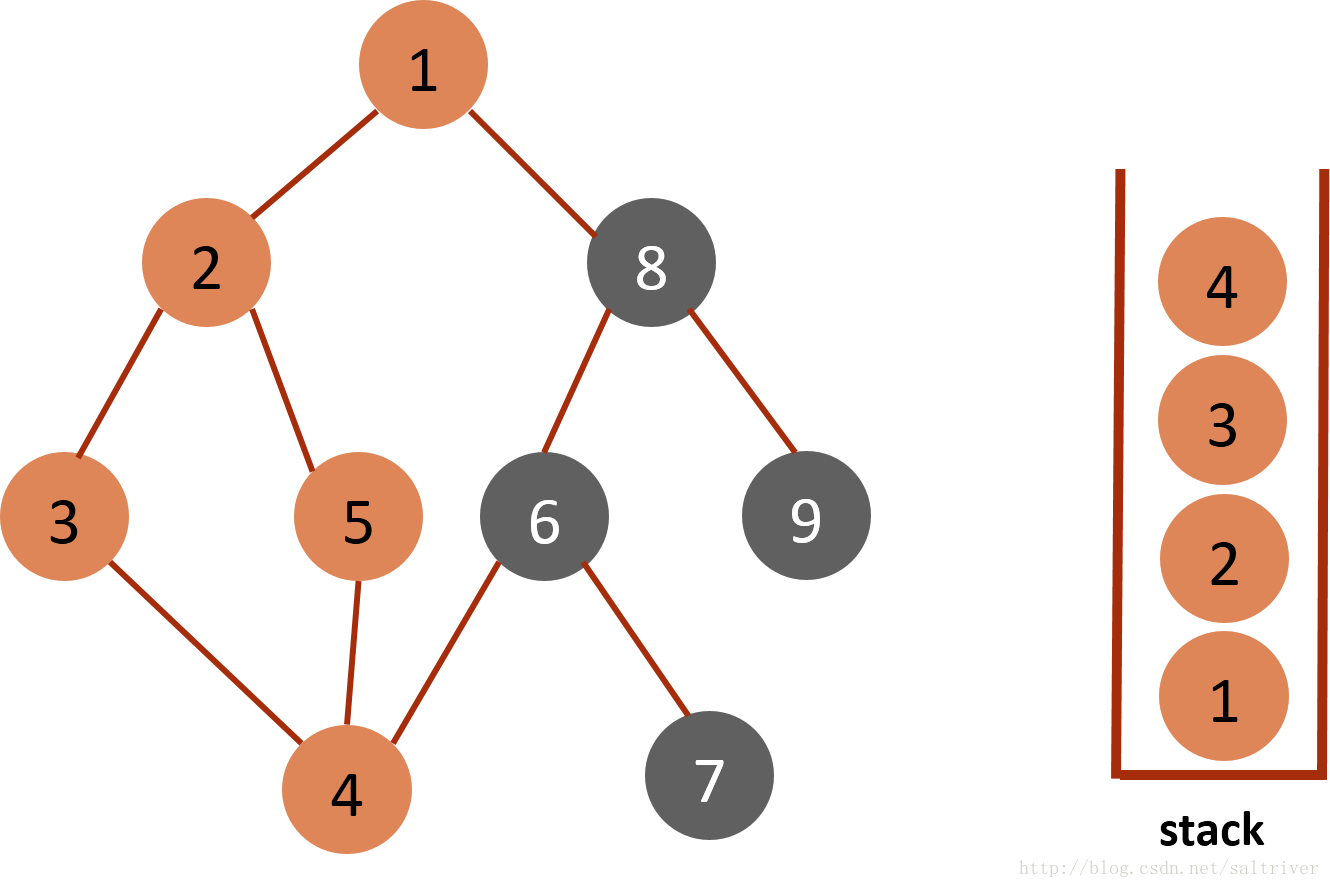
(7)当前stack栈顶的节点是4,找出与节点4邻接的节点,有3,5,6三个节点,节点3,5都已遍历过,排除;选中的是节点6,标记为已遍历,然后放入stack中。

(8)当前stack栈顶的节点是6,找出与节点6邻接的节点,有4,7,8三个节点,4已遍历,按照规则选中的是7,标记为已遍历,然后放入stack中。

(9)当前stack栈顶的节点是7,找出与节点7邻接的节点,只有节点6,已遍历过,因此没有尚未遍历的邻接点,将节点7从stack中弹出。

(10)当前stack栈顶的节点是6,找出与节点6邻接的节点,有节点7,8,7已遍历过,因此将节点8放入stack中。

(11)当前stack栈顶的节点是8,找出与节点8邻接的节点,有节点1,6,9,1,6已遍历过,因此将节点9放入stack中。
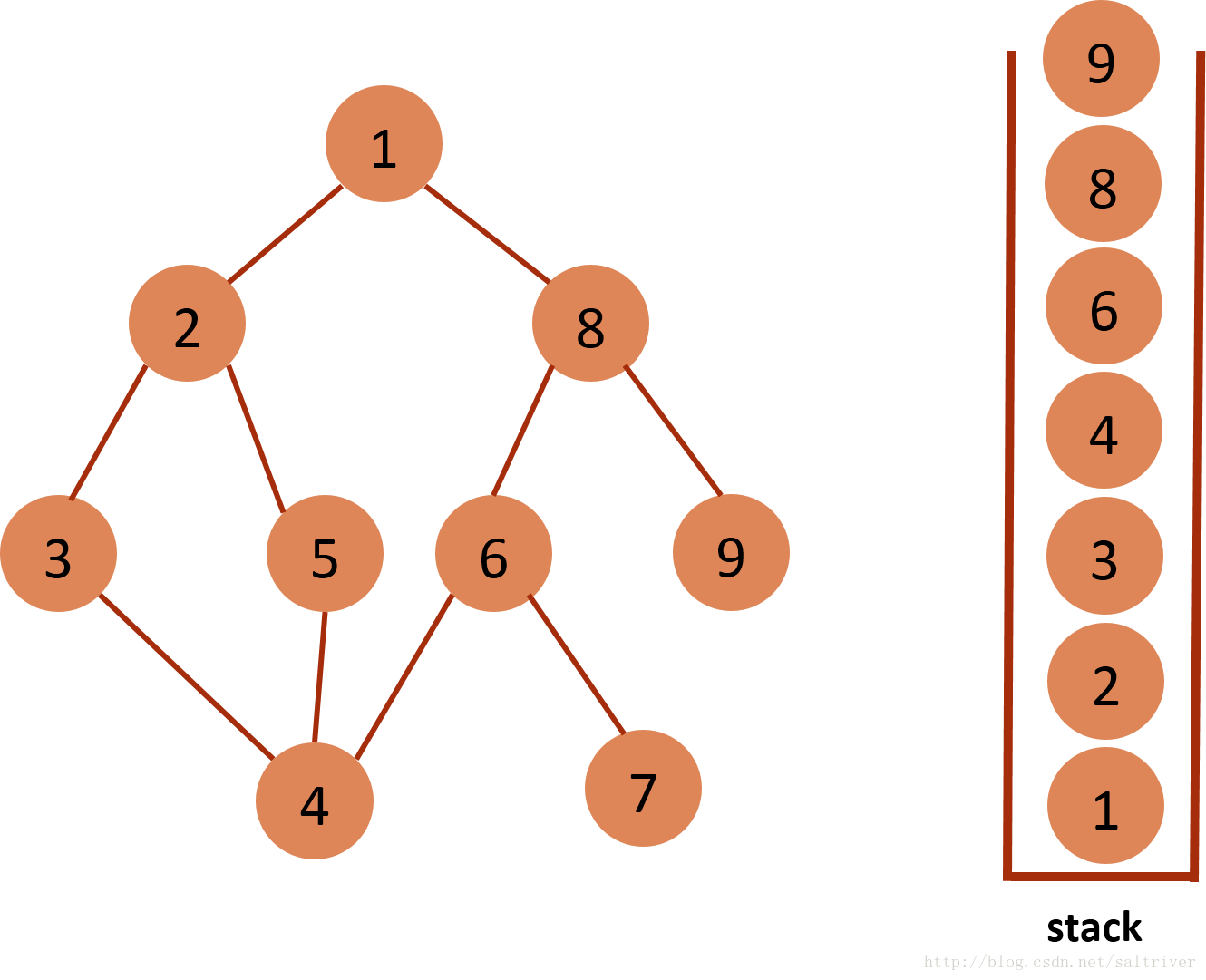
(12)当前stack栈顶的节点是9,没有尚未遍历的邻接点,将节点9弹出,依次类推,栈中剩余节点8,6,4,3,2,1都没有尚未遍历的邻接点,都将弹出,最后栈为空。
(13)DFS遍历完成。
//邻接矩阵代码
void DFS(MGraph g, int v)//深度遍历
{
visited[v] = 1;//建立visited数组存储已访问的结点信息
if (flag == 0)//控制空格输出
{
cout << v;
flag = 1;
}
else
{
cout << " " << v;
}
for (int i = 1; i <= g.n; i++)
{
if (g.edges[v][i] == 1 && visited[i] == 0)//未访问且两点之间连通
{
DFS(g, i);
}
}
}
//邻接表代码
void DFS(AdjGraph* G, int v) //v节点开始深度遍历
{
ArcNode* p;
visited[v] = 1; //访问完赋予1值
if (!flag)
{
cout << v;
flag = 1;
}
else cout << " " << v;
p = G->adjlist[v].firstarc; //p指向顶点v的第一个邻接点
while (p!=NULL) //遍历
{
if (!visited[p->adjvex])
DFS(G, p->adjvex);
p = p->nextarc; //p指向v的下一个邻接点
}
}
深度遍历适用哪些问题的求解。(可百度搜索)
1.全排列问题
2.连通分量包含顶点数量问题
3.二维数组寻找最短路径问题
4.检测无向图中是否含环问题
5.棋盘问题
1.2.2 广度优先遍历
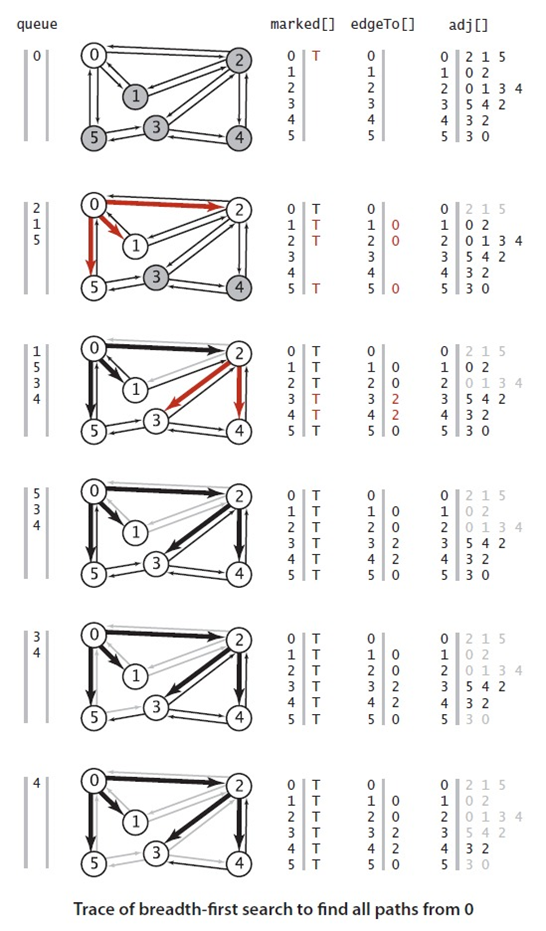
广度遍历代码:
//邻接矩阵代码:
void BFS(MGraph g, int v)
{
int i, k;
int cur_node;
int queue[MAXV];
int front, rear;
front = rear = 0; //建立队列
visited[0] = 0; //初始化0
visited[v - 1] = 1;
queue[rear++] = v;//enqueue
cout << v;
while (front != rear)
{
cur_node = queue[front++];
for (i = 0; i < g.n; i++)
{
if (visited[i] == 0 && g.edges[cur_node-1][i] != 0)
{
cout << " " << i + 1;
queue[rear++] = i + 1;
visited[i] = 1;
}
}
}
}
//邻接表代码
void BFS(AdjGraph *G, int v)//v节点开始广度遍历
{
ArcNode *p;//新建结点储存当前信息
queue<int>q;
cout << v;
q.push(v);
visited[v] = 1;//已访问
int w;
while (!q.empty())
{
w = q.front();
q.pop();
p = G->adjlist[w].firstarc;
while (p != NULL)//遍历当前链
{
if (visited[p->adjvex] == 0)//未访问过
{
visited[p->adjvex] = 1;
cout << " " << p->adjvex;
q.push(p->adjvex);
}
p = p->nextarc;
}
}
}
广度遍历适用哪些问题的求解。(可百度搜索)
1.迷宫问题
2.两顶点间最短路径问题
1.3 最小生成树
用自己语言描述什么是最小生成树。
1.3.1 Prim算法求最小生成树

实现Prim算法的2个辅助数组:
closest数组:表示边的最小权值
lowcost数组:存放最优的边
Prim算法代码:
//最小生成树Prim算法代码:
void Prim(Graph G)
{
int v=0;//初始节点
closedge C[MaxVerNum];
int mincost = 0; //记录最小生成树的各边权值之和
//初始化
for (int i = 0; i < G.vexnum; i++)
{
C[i].adjvex = v;
C[i].lowcost = G.Edge[v][i];
}
cout << "最小生成树的所有边:"<< endl;
//初始化完毕,开始G.vexnum-1次循环
for (int i = 1; i < G.vexnum; i++)
{
int k;
int min = INF;
//求出与集合U权值最小的点 权值为0的代表在集合U中
for (int j = 0; j<G.vexnum; j++)
{
if (C[j].lowcost != 0 && C[j].lowcost<min)
{
min = C[j].lowcost;
k = j;
}
}
//输出选择的边并累计权值
cout << "(" << G.Vex[k] << "," << G.Vex[C[k].adjvex]<<") ";
mincost += C[k].lowcost;
//更新最小边
for (int j = 0; j<G.vexnum; j++)
{
if (C[j].lowcost != 0 && G.Edge[k][j]<C[j].lowcost)
{
C[j].adjvex = k;
C[j].lowcost= G.Edge[k][j];
}
}
}
cout << "最小生成树权值之和:" << mincost << endl;
Prim算法:
时间复杂度为o(n^2)。
适用于稠密图的最小生成树,适用于邻接矩阵。
因为Prim算法需要频繁的取边,使用对应边的权值。
1.3.2 Kruskal算法求解最小生成树
实现Kruskal算法的辅助数据结构:
辅助数组vest用于记录起始点和终止点的下标,通过改变数组的值来改变顶点的所属集合。
Kruskal算法代码:
//最小生成树Kruskal算法代码
void Kruskal(Graph G)
{
sort(l.begin(), l.end(),cmp);
int verSet[MaxVerNum];
int mincost = 0;
for (int i = 0; i < G.vexnum; i++)
verSet[i] = i;
cout << "最小生成树所有边:" << endl; //对各边进行查看
int all = 0;
for (int i = 0; i < G.arcnum; i++)
{
if (all == G.vexnum - 1)break;
int v1 = verSet[l[i].from];
int v2 = verSet[l[i].to]; //连接两连通分支
if (v1 != v2)
{
cout << "(" << l[i].from << "," << l[i].to << ") ";
mincost += l[i].weight;
for (int j = 0; j < G.vexnum; j++)
{
if (verSet[j] == v2)verSet[j] = v1;
}
all++; //连通分支合并
}
}
cout << "最小生成树权值之和:" <<mincost<<endl;
Kruskal算法时间复杂度:
<基于上述图结构求Kruskal算法生成的最小生成树的边序列
Kruskal算法时间复杂度为O(n^2)
1.4 最短路径
1.4.1 Dijkstra算法求解最短路径
基于上述图结构,求解某个顶点到其他顶点最短路径。(结合dist数组、path数组求解)
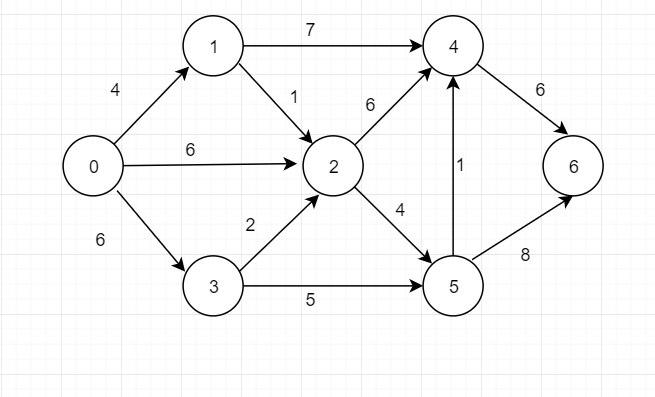

Dijkstra算法辅助数据结构:
<dist[]:记录当前顶点到对象顶点的当前最短路径长度
path[]:记录对应顶点的前驱顶点
Dijkstra算法(贪心算法)求解最优解问题:
void Dijkstra(MGraph g, int v)//源点v到其他顶点最短路径
{
int* S = new int[g.n];
int* dist = new int[g.n];
int* path = new int[g.n];
int i,j,k,MINdis;
//初始化各个数组
for (i = 0; i < g.n; i++)
{
S[i] = 0;
dist[i] = g.edges[v][i];//
//不需要进行分类,因为不存在边的权值已经初始化为INF
if (g.edges[v][i] < INF)
{
path[i] = v;
}
else
{
path[i] = -1;
}
}
S[v] = 1, dist[v] = 0, path[v] = 0;
for (i = 0; i < g.n-1; i++)
{
//根据dist中的距离从未选顶点中选择距离最小的纳入
MINdis = INF;
for (j = 0; j < g.n; j++)
{
if (S[j] == 0 && dist[j] < MINdis)
{
MINdis = dist[j];
k = j;
}
}
S[k] = 1;
//纳入新顶点后更新dist信息和path信息
for (j = 0; j < g.n; j++)
{
if (S[j] == 0)//针对还没被选中的顶点
{
if (g.edges[k][j] < INF //新纳的顶点到未被选中的顶点有边
&& dist[k] + g.edges[k][j] < dist[j])//源点到k的距离加上k到j的距离比当前的源点到j的距离短
{
dist[j] = dist[k] + g.edges[k][j];
path[j] = k;
}
}
}
}
}
Dijkstra算法的时间复杂度:单顶点时间复杂度为O(n2),对n个顶点时间复杂度为O(n3)。
使用邻接矩阵存储结构来存储,算法中需要直接获取边的权值,而邻接矩阵获取权值的时间复杂度低于邻接表存储结构。
1.4.2 Floyd算法求解最短路径
Floyd算法解决问题:
<1.求解顶点与顶点间的最短路径以及长度问题。
2.无向图的最小环问题
Floyd算法辅助数据结构:
A[][]用于存放两个顶点之间的最短路径
path[][],path数组用于存放其的前继结点。
Floyd算法
void ShortestPath_Floyd(MGraph G, Patharc *P, ShortPathTable *D)
{
int v,w,k;
for(v=0; v<G.numVertexes; ++v) /* 初始化D与P */
{
for(w=0; w<G.numVertexes; ++w)
{
(*D)[v][w]=G.arc[v][w]; /* D[v][w]值即为对应点间的权值 */
(*P)[v][w]=w; /* 初始化P */
}
}
for(k=0; k<G.numVertexes; ++k)
{
for(v=0; v<G.numVertexes; ++v)
{
for(w=0; w<G.numVertexes; ++w)
{
if ((*D)[v][w]>(*D)[v][k]+(*D)[k][w])
{/* 如果经过下标为k顶点路径比原两点间路径更短 */
(*D)[v][w]=(*D)[v][k]+(*D)[k][w];/* 将当前两点间权值设为更小的一个 */
(*P)[v][w]=(*P)[v][k]; /* 路径设置为经过下标为k的顶点 */
}
}
}
}
}
最短路径算法:
SPFA 算法:
<SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环。
最坏情况下复杂度和朴素 Bellman-Ford 相同,为 O(VE)。
//伪代码
ProcedureSPFA;
Begin
initialize-single-source(G,s);
initialize-queue(Q);
enqueue(Q,s);
while not empty(Q) do begin
u:=dequeue(Q);
for each v∈adj[u] do begin
tmp:=d[v];
relax(u,v);
if(tmp<>d[v])and(not v in Q)then enqueue(Q,v);
end;
end;
End;
//C++代码
#include<iostream>
#include<vector>
#include<list>
using namespace std;
struct Edge
{
int to,len;
};
bool spfa(const int &beg,//出发点
const vector<list<Edge> > &adjlist,//邻接表,通过传引用避免拷贝
vector<int> &dist,//出发点到各点的最短路径长度
vector<int> &path)//路径上到达该点的前一个点
//没有负权回路返回0
//福利:这个函数没有调用任何全局变量,可以直接复制!
{
const int INF=0x7FFFFFFF,NODE=adjlist.size();//用邻接表的大小传递顶点个数,减少参数传递
dist.assign(NODE,INF);//初始化距离为无穷大
path.assign(NODE,-1);//初始化路径为未知
list<int> que(1,beg);//处理队列
vector<int> cnt(NODE,0);//记录各点入队次数,用于判断负权回路
vector<bool> flag(NODE,0);//标志数组,判断是否在队列中
dist[beg]=0;//出发点到自身路径长度为0
cnt[beg]=flag[beg]=1;//入队并开始计数
while(!que.empty())
{
const int now=que.front();
que.pop_front();
flag[now]=0; //将当前处理的点出队
for(list<Edge>::const_iterator//用常量迭代器遍历邻接表
i=adjlist[now].begin(); i!=adjlist[now].end(); ++i)
if(dist[i->to]>dist[now]+i->len) //不满足三角不等式
{
dist[i->to]=dist[now]+i->len; //更新
path[i->to]=now;//记录路径
if(!flag[i->to])//若未在处理队列中
{
if(NODE==++cnt[i->to])return 1; //计数后出现负权回路
if(!que.empty()&&dist[i->to]<dist[que.front()])//队列非空且优于队首(SLF)
que.push_front(i->to); //放在队首
else que.push_back(i->to); //否则放在队尾
flag[i->to]=1;//入队
}
}
}
return 0;
}
int main()
{
int n_num,e_num,beg;//含义见下
cout<<"输入点数、边数、出发点:";
cin>>n_num>>e_num>>beg;
vector<list<Edge> > adjlist(n_num,list<Edge>());//默认初始化邻接表
for(int i=0,p; i!=e_num; ++i)
{
Edge tmp;
cout<<"输入第"<<i+1<<"条边的起点、终点、长度:";
cin>>p>>tmp.to>>tmp.len;
adjlist[p].push_back(tmp);
}
vector<int> dist,path;//用于接收最短路径长度及路径各点
if(spfa(beg,adjlist,dist,path))cout<<"图中存在负权回路\n";
else for(int i=0; i!=n_num; ++i)
{
cout<<beg<<"到"<<i<<"的最短距离为"<<dist[i]<<",反向打印路径:";
for(int w=i; path[w]>=0; w=path[w])cout<<w<<"<-";
cout<<beg<<'\n';
}
}
pascal代码
const
maxp=10000;{最大结点数}
var{变量定义}
p,c,s,t:longint;{p,结点数;c,边数;s:起点;t:终点}
a,b:array[1..maxp,0..maxp]of longint;{a[x,y]存x,y之间边的权;b[x,c]存与x相连的第c个边的另一个结点y}
d,m:array[1..maxp]of integer;{d:队列,m:入队次数标记}
v:array[1..maxp]of boolean;{是否入队的标记}
dist:array[1..maxp]of longint;{到起点的最短路}
head,tail:longint;{队首/队尾指针}
procedure init;
var
i,x,y,z:longint;
begin
read(p,c);
for i:=1 to c do begin
readln(x,y,z);{x,y:一条边的两个结点;z:这条边的权值}
inc(b[x,0]);b[x,b[x,0]]:=y;a[x,y]:=z;{b[x,0]:以x为一个结点的边的条数}
inc(b[y,0]);b[y,b[y,0]]:=x;a[y,x]:=z;
end;
readln(s,t);{读入起点与终点}
end;
procedure spfa(s:longint);{SPFA}
var
i,j,now:longint;
begin
fillchar(d,sizeof(d),0);
fillchar(v,sizeof(v),false);
for j:=1 to p do dist[j]:=maxlongint;
dist[s]:=0; v[s]:=true; d[1]:=s; {队列的初始状态,s为起点}
head:=1; tail:=1;
while head<=tail do{队列不空}
begin
now:=d[head];{取队首元素}
for i:=1 to b[now,0] do
if dist[b[now,i]]>dist[now]+a[now,b[now,i]] then
begin
dist[b[now,i]]:=dist[now]+a[now,b[now,i]];{修改最短路}
if not v[b[now,i]] then{扩展结点入队}
begin
inc(m[b[now,i]]);
if m[b[now,i]]=p then begin writeln('no way');halt;end;
{同一节点入队次数超过p,存在负环}
inc(tail);
d[tail]:=b[now,i];
v[b[now,i]]:=true;
end;
end;
v[now]:=false;{释放结点,一定要释放掉,因为这节点有可能下次用来松弛其它节点}
inc(head);{出队}
end;
end;
procedure print;
begin
writeln(dist[t]);
end;
begin
init;
spfa(s);
print;
end.
比较:与bfs算法比较,复杂度相对稳定。但在稠密图中复杂度比迪杰斯特拉算法差。
1.5 拓扑排序
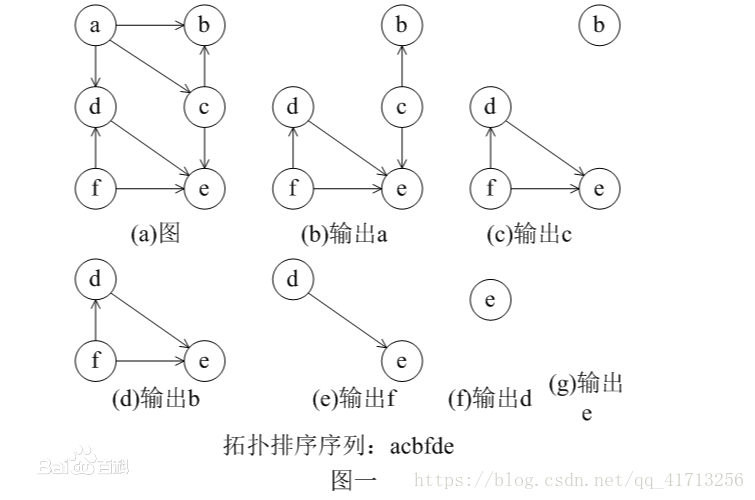
拓扑排序结构体代码:
typedef struct Vnode
{
Vertex data; //顶点信息
int count;
ArcNode* firstarc; //指向第一条边
} VNode; //邻接表头节点类型
拓扑排序代码删除入度为0的结点
void TopSort(AdjGraph *G)//邻接表拓扑排序。注:需要在该函数开始计算并初始化每个节点的入度,然后再进行拓扑排序
{
int node[MAXV];
int counts = 0;
int top = -1;
int stacks[MAXV];
ArcNode *p;
int i, j, k = 0;
for (i = 0; i < G->n; i++)//初始化count
{
G->adjlist[i].count = 0;
}
for (i = 0; i < G->n; i++)
{
p = G->adjlist[i].firstarc;
while (p)//计算每个结点入度
{
G->adjlist[p->adjvex].count++;
p = p->nextarc;
}
}
for (i = 0; i < G->n; i++)
{
if (G->adjlist[i].count == 0)//结点为0入栈
{
stacks[++top] = i;
}
}
while (top > -1)
{
i = stacks[top--];
node[k++] = i;//进入数组
counts++;
p = G->adjlist[i].firstarc;
while (p)
{
j = p->adjvex;
G->adjlist[j].count--;//该节点入度-1
if (G->adjlist[j].count == 0)
{
stacks[++top] = j;
}
p = p->nextarc;
}
}
if (counts < G->n)//判断个数是否符合
{
cout << "error!";
}
else
{
for (i = 0; i < k; i++)
{
cout << node[i];
if (i != k - 1)
{
cout << " ";
}
}
}
}
用拓扑排序代码检查一个有向图有环路
bool topologicalSort()
{
cout << "有向图的拓扑排序:" << endl;
stack<int> inDegree0VexStack;
for (int i = 0; i < vexNum; i++)
{
if (InDegree[i] == 0)
{
inDegree0VexStack.push(i);
}
}
int count = 0;//对输出顶点计数
while (!inDegree0VexStack.empty())
{
int i = inDegree0VexStack.top();//输入i号顶点,并计数
inDegree0VexStack.pop();
//cout << vecNodes[i]->Alphabet << " ";
cout << i + 1 << " ";
++count;
for (int j = 0; j < vexLists[i]->size(); j++)
{//对i号顶点的每一个邻接顶点j的入度减1,即i->i的邻接顶点
int nodeNum = vexLists[i]->at(j)->num;
if ((--InDegree[nodeNum] == 0))
{//若入度减到了0,则入栈
inDegree0VexStack.push(nodeNum);
}
}
}
if (count < vexNum)
{//该有向图有环
return true;
}
else
{//该有向图无环,可将所有顶点按拓扑有序输出。
return false;
}
}
bool hasLoop()
{
if (topologicalSort())
{
cout << endl;
cout << "该有向图有环!" << endl;
return true;
}
else
{
cout << endl;
cout << "该有向图无环!" << endl;
return false;
}
}//topologicalSort
1.6 关键路径

AOE-网
<有向图中,用顶点表示活动,用有向边表示活动之间开始的先后顺序,则称这种有向图为AOV(Activity On Vertex)网络;AOV网络可以反应任务完成的先后顺序(拓扑排序)。
在AOV网的边上加上权值表示完成该活动所需的时间,则称这样的AOV网为AOE(Activity On Edge)网
关键路径概念:
路径上各个活动所持续的时间之和称为路径长度,从源点到汇点具有最大长度的路径叫关键路径
关键活动:
在关键路径上的活动叫关键活动。
2.PTA实验作业(4分)
2.1 六度空间(2分)
<7-2 六度空间 (30 分)
“六度空间”理论又称作“六度分隔(Six Degrees of Separation)”理论。这个理论可以通俗地阐述为:“你和任何一个陌生人之间所间隔的人不会超过六个,也就是说,最多通过五个人你就能够认识任何一个陌生人。”如图1所示。
图1 六度空间示意图
“六度空间”理论虽然得到广泛的认同,并且正在得到越来越多的应用。但是数十年来,试图验证这个理论始终是许多社会学家努力追求的目标。然而由于历史的原因,这样的研究具有太大的局限性和困难。随着当代人的联络主要依赖于电话、短信、微信以及因特网上即时通信等工具,能够体现社交网络关系的一手数据已经逐渐使得“六度空间”理论的验证成为可能。
假如给你一个社交网络图,请你对每个节点计算符合“六度空间”理论的结点占结点总数的百分比。
输入格式:
输入第1行给出两个正整数,分别表示社交网络图的结点数N(1<N≤10^3,表示人数)、边数M(≤33×N,表示社交关系数)。随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个结点的编号(节点从1到N编号)。
输出格式:
对每个结点输出与该结点距离不超过6的结点数占结点总数的百分比,精确到小数点后2位。每个结节点输出一行,格式为“结点编号:(空格)百分比%”。
输入样例:
10 9
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
输出样例:
1: 70.00%
2: 80.00%
3: 90.00%
4: 100.00%
5: 100.00%
6: 100.00%
7: 100.00%
8: 90.00%
9: 80.00%
10: 70.00%
2.1.1 伪代码
伪代码
用邻接矩阵构图
初始化,对每条边赋值为1
while (!qu.empty() && level < 6)
{
循环遍历顶点
{
若该顶点未被访问过,且该顶点与i之前存在边
{
count++;//满足六度空间理论的结点数+1
i出栈
visited[i] = 1;//标记结点i为已访问
tail = i;
}
}
if (last == temp)
{
该层遍历完成,level++
last = tail;
}
}
循环遍历每个顶点
{
BFS(每个顶点)
输出: (和所求顶点距离小于等于6的顶点数) * 100.00 / 总顶点数
}
2.1.2 提交列表

2.1.3 本题知识点
链表的相关操作
广度优先遍历
邻接矩阵的构建
2.2 村村通

2.2.1 伪代码
int main()
{
输入边数和顶点数;
Create(n, e);
int num=0;
num = Prim(n, e);
}
void Create(int n, int e)
{
对矩阵初始化;
修改矩阵;
}
int Prim(int n, int e)
{
int closet[];//保存顶点下标
int lowcost[];//保存权值
int cost = 0;
lowcost[1] = 0;
lowcost[1] = 0;
初始化lowcost[]和closet;
for (i = 2; i <= 2; i++)
{
初始化min,j,k;
while (j < n)
{
找到权值最小的点记录下标;
}
if (判断下标是否改变, 若有证明连通)
{
记录cost和访问顶点操作;
}
else return -1;
修改lowcost和closet;
}
}
2.2.2 提交列表




 浙公网安备 33010602011771号
浙公网安备 33010602011771号