《An Energy-Efficient Logarithmic-Posit-Based In-SRAM Computing for Neural Network Acceleration》（一）

以下是对论文《An Energy-Efficient Logarithmic-Posit-Based In-SRAM Computing for Neural Network Acceleration》的中文分析，依照你的六点要求逐条展开：

1. 论文主要内容与研究方向

本论文提出了一种基于Logarithmic-Posit（LP）格式的SRAM-内存计算（CIM）宏单元，旨在提升神经网络（NN）加速中的能效和面积效率。研究方向聚焦于将乘法-加法（MAC）操作迁移至对数域，以简化硬件并适应深度学习中数据分布的动态特性。

2. 研究方法与核心模块（含图）

研究方法主要包括三项技术创新：

  • Logarithmic-Posit（LP）格式替代传统FP/BF16格式，使乘法转为指数加法。
  • 位并行LP解码器减少CIM阵列计算瓶颈。
  • 位级指数比较（Bit-wise Comparison）对齐加法器树替代传统比较树，降低能耗和面积开销。

原文核心架构图：

【图1：LP-SRAM-CIM整体架构】

![](attachment:/mnt/data/Chang 等 - 2024 - An Energy-Efficient Logarithmic-Posit-Based In-SRA.pdf_page-2.png)

解码和对数转换细节：

【图2：LP解码器与Log-to-Linear变换器结构】

![](attachment:/mnt/data/Chang 等 - 2024 - An Energy-Efficient Logarithmic-Posit-Based In-SRA.pdf_page-3.png)

位级指数比较逻辑图：

【图3(a)：位级对齐逻辑】

![](attachment:/mnt/data/Chang 等 - 2024 - An Energy-Efficient Logarithmic-Posit-Based In-SRA.pdf_page-5.png)

3. 研究结果与实验分析

实验平台：28nm CMOS工艺，128×128（16Kb）CIM阵列
对比项目：

  • INT8-CIM（21年ISSCC）【1】
  • BF16-CIM ReDCIM（22年ISSCC）【2】
  • BF16-CIM DBcell（23年ISSCC）【3】
模型/平台 本文提出 LP-CIM INT-CIM [1] BF16-CIM [2] BF16-CIM [3]
能效提升（相对） - 1.68× 2.41× 3.50×
面积效率提升（相对） - 1.05× 2.56× 2.30×
ResNet-18准确率 75.05% 75.17% 75.32% 75.32%
EfficientNet-B0准确率 73.66% 无法INT8量化 76.53% 76.53%

尽管LP(8,1)格式在EfficientNet-B0下略有精度损失（73.66%），但其仍保持可接受的精度，且能效和面积效率大幅优于其他方案。

4. 论文出处与会议等级

  • 会议名称：IEEE International Conference on Integrated Circuits, Technologies and Applications (ICTA 2024)
  • 会议级别：IEEE会议，目前不属于CCF推荐会议，但为国际集成电路方向活跃会议，具有一定影响力。
  • DOI链接：10.1109/ICTA64028.2024.10860597

5. 是否有开源代码地址

论文中未明确提供开源代码地址，相关实现主要由上海交通大学微纳电子系完成。可尝试联系通信作者Yanan Sun（sunyanan@sjtu.edu.cn）以了解更多。

6. 相关内容原文出处

  • 架构图、模块解析见 Fig.1, Fig.2（第2–3页）
  • Bit-wise对齐机制详见 Fig.3(a)（第5页）
  • 性能对比结果见 Fig.3(b) 和 Table I（第5页）
  • LP数据格式定义与计算方式见公式(1)（第3页）

好的，我来详细解释论文中Posit格式是如何使用的，并且对应给出原文出处。

1. 论文中Posit使用概览

在本论文中，Posit格式的作用是：

  • 基础作用：
    采用Posit编码规则设计了一种Logarithmic-Posit（LP）格式。
    Posit自身具备“压缩大数、细分小数”的自适应动态范围特性，非常适合神经网络中数据分布的特点。

  • 具体实现：

    • LP格式沿用了Posit的基本结构（Sign + Regime + Exponent + Fraction），
    • 与标准Posit不同，LP格式把小数部分（mantissa）转换到对数域，形成Log-Fraction，用于简化乘法为指数加法。
    • 目的是：保留Posit的动态范围自适应优势，但在硬件中进一步降低复杂度与能耗。

  • 在硬件中应用的位置：

    • 所有输入数据和权重数据都预量化为LP(8,1)格式。
    • 通过LP解码器解码为1位符号位+9位指数（包括对数分数）。
    • 乘法操作被替换成指数加法，大幅减少硬件开销。

2. 论文中关于Posit使用的详细出处

【1】LP数据格式定义与Posit关系

  • 原文位置：第3页，第II.B节《Addition-based LP Multiplication》

  • 原文内容（截图来源于文件第3页）：

    “The LP data is defined by the bit width n and the exponent size es, consisting of 4 fields, namely sign, regime, exponent and logarithmic fraction, as shown in Fig. 2(b). The LP [5] data format follows the encoding rule of the standard posit format while expressing the linear mantissa (1.f) in the log domain as a fixed-point fraction exponent of the power of two as f’, where f’=log2(1.f).”

🔵 解释：

  • LP格式继承了标准Posit格式的字段结构。
  • 主要变化是：Mantissa（尾数）不再是线性数，而是它的对数值log(1.f)。
  • 这样可以用简单的加法代替复杂的乘法。

【2】LP解码器工作过程（基于Posit规则）

  • 原文位置：第3-4页，Fig. 2(a)、Fig. 2(b)

  • 原文内容：

    “During the decoding, the LP data is firstly converted into the 2's complement and inverted according to the first bit of regime...”

🔵 解释：

  • LP解码器按照Posit的Regime编码规则解析。
  • 具体解码步骤：
    1. 根据首位判断是否需要取反。
    2. 计算Regime值。
    3. 提取Exponent和Fraction部分。
  • 解码后得到9位对数指数。

【3】Posit（LP）在CIM阵列中的应用

  • 原文位置：第2页，第II.A节《SRAM-CIM Macro Overview》

  • 原文内容：

    “Then each 8-bit LP input is fed into an LP decoder to generate 1b sign and 9b LP-exponent signals per cycle in a bit-parallel manner…”

🔵 解释：

  • 输入数据采用LP(8,1)格式。
  • 直接在硬件中位并行处理，不再像传统方法那样逐位串行处理，大大提升了吞吐率和能效。

【4】与标准Posit格式的差异说明

  • 原文位置：第3页，公式(1)
  • 公式内容：

[
\text{Value} = (-1)^{\text{sign}} \times 2{2{\text{regime}}} \times 2^{\text{exponent}} \times 2^{\text{fraction}}
]

🔵 解释：

  • 虽然公式外观看似与标准Posit相似，
  • 但区别在于：fraction部分是log(1.f)形式的，而不是传统线性f。
  • 这正是“Logarithmic-Posit”名字的由来。

3. 总结一下论文中的Posit使用特色

项目 内容
使用格式 LP(8,1)，基于标准Posit定义
变化 小数部分用对数表示（Log Fraction）
硬件处理 符号提取，Regime解码，Exponent与Log-Fraction分离
运算替代 乘法→指数加法，显著降低功耗和面积
应用位置 输入数据、权重数据，SRAM-CIM阵列计算

1

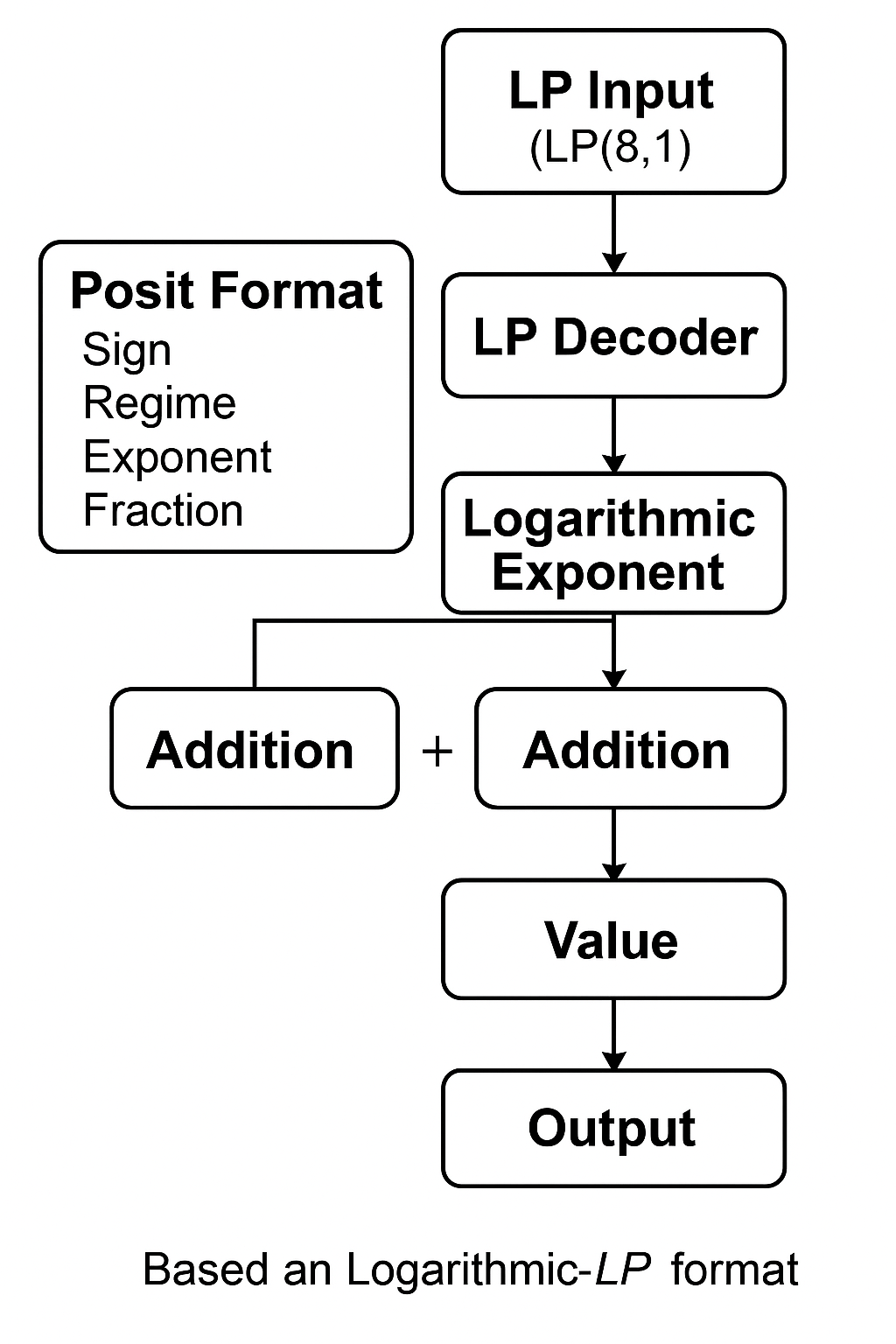
可以总结为：

✅ 本文在Posit使用上的核心创新，就是：

  • 不是直接用标准Posit做计算，
  • 而是在Posit编码规则基础上，
  • 将乘法操作转化为对数域上的加法，
  • 以进一步简化硬件（特别是乘法器部分），降低能耗和面积，提高速度。

具体来说，标准Posit格式虽然本身已经在数值范围和精度上优于传统浮点，但在硬件实现时，仍然需要复杂的乘法器。而本文提出的Logarithmic-Posit（LP）格式，做了两步关键改动：

  1. 保持Posit的数据组织方式（Sign + Regime + Exponent + Fraction），
  2. 将Fraction（尾数）取对数，使得在CIM阵列中可以用简单的指数加法代替乘法。

这样，不仅保留了Posit的动态范围优势，
而且大幅降低了硬件复杂度，实现了高能效SRAM-CIM加速。

🔵 论文中明确对应的出处：

  • 第3页，II.B节（Addition-based LP Multiplication）
  • 原文关键句：

    "The LP data format follows the encoding rule of the standard posit format while expressing the linear mantissa (1.f) in the log domain as a fixed-point fraction exponent of the power of two as f’, where f’=log2(1.f)."

posted @ 2025-04-29 03:01  江左子固  阅读(50)  评论(0)    收藏  举报