《Universal Number Posit Arithmetic Generator on FPGA》（二）

Posit编码过程分析

这段文字描述了如何从浮点数参数（符号、指数、尾数）构造Posit的二进制表示。以下是分步解析：

---

1. 参数定义

• 输入参数：
  • ( S_{FP} ): 浮点数的符号位（直接作为Posit的符号位）。
  • ( R_O ): Regime偏移量（决定Regime的游程长度）。
  • ( E_O ): 指数偏移量（显式指数部分的数值）。
  • ( M_{FP} ): 浮点数的尾数（需调整适应Posit的尾数位）。

---

2. 编码步骤详解

步骤1：符号位处理

• ( S_{FP} ) 直接作为Posit的最高有效位（MSB）。
• 示例：若浮点数为负数，则Posit符号位为1。

步骤2：生成Regime位序列

• 根据指数( Exp[E] )的符号生成重复的0或1序列：
  • 负指数 → 生成全0序列（如000...）。
  • 正指数 → 生成全1序列（如111...）。
• 序列长度为( N = |Exp[E]| )，即指数的绝对值。
• 示例：若( Exp[E] = -3 )，则生成3位0序列000。

步骤3：添加Regime终止位

• 在Regime序列末尾添加一个终止位（与Regime序列相反）：
  • 若Regime为全0，则终止位为1。
  • 若Regime为全1，则终止位为0。
• 示例：Regime序列000 → 终止位1 → 组合为0001。

步骤4：构造指数-尾数字段

• 合并( Exp[E] )、( E_O )、( M_{FP} )为N位字段，低位补零：
  • 字段结构：[Exp[E] | E_O | M_FP]（具体位分配需根据Posit格式调整）。
• 示例：若N=8，且( Exp[E] )占2位，( E_O )占1位，( M_{FP} )占5位，则组合为Exp[E](2) + E_O(1) + M_FP(5)，不足位补零。

步骤5：生成REM字段

• 将Regime序列（高位N位）与指数-尾数字段（低位N位）合并为2N位的REM字段。
• 示例：若Regime序列为0001（4位），指数-尾数字段为0101100（4位），则REM = 0001 0101100（总长度8位）。

步骤6：动态右移与符号处理

• 右移操作：根据( R_O )的值将REM右移，插入Regime序列到低位。
  • 目的：调整数值的动态范围，确保指数和尾数对齐。
• 补码处理：若符号位为负（( S_{FP}=1 )），对REM取2的补码。
• 最终截取：取REM[N-1:1]（去除终止位）作为Regime、指数和尾数的组合。

步骤7：合成Posit字

• 将符号位与处理后的REM字段合并，并处理特殊情况：
  • 零值：若数值为零，所有位为0。
  • 无穷大（NaR）：若数值超出范围，编码为特定模式（如全1）。

---

3. 关键技术与挑战

• 动态Regime编码：
  Regime的长度和值由指数动态决定，需通过游程编码和终止位实现，增加了硬件实现的复杂度。
• 符号与补码处理：
  负数的补码操作需确保数值正确性，尤其是在右移和位截取时可能引入误差。
• 特殊值处理：
  需单独处理零和NaR，避免与正常数值混淆。

---

4. 示例演算（以Posit8为例）

假设输入参数：

• ( S_{FP}=0 )（正数），( Exp[E]=-2 )，( E_O=1 )，( M_{FP}=10110 )。

步骤执行：

1. 符号位：0。
2. Regime序列：00（( N=2 )，负指数生成全0）。
3. 终止位：1 → Regime字段为001。
4. 指数-尾数字段：合并( Exp[E]=-2 )、( E_O=1 )、( M_{FP}=10110 )，假设分配为Exp[E](2) + E_O(1) + M_FP(5) → 10 1 10110，补零后为10110110（8位）。
5. REM字段：高位N位=001，低位N位=10110110 → 合并为00110110110（需调整位宽）。
6. 右移( R_O=2 )位 → 插入Regime到低位，结果为00110110。
7. 最终Posit字：符号位0 + REM字段 → 0 00110110。

---

5. 总结

此编码流程通过动态调整Regime和指数尾数，实现了Posit的高效数值表示。其核心优势在于：

• 动态范围优化：通过Regime机制覆盖更广的指数范围。
• 精度弹性：尾数位随数值大小动态分配，小数值精度更高。
  但需注意：
• 硬件开销：动态编码需要复杂的逻辑电路。
• 标准化挑战：需统一实现细节以确保跨平台兼容性。

---

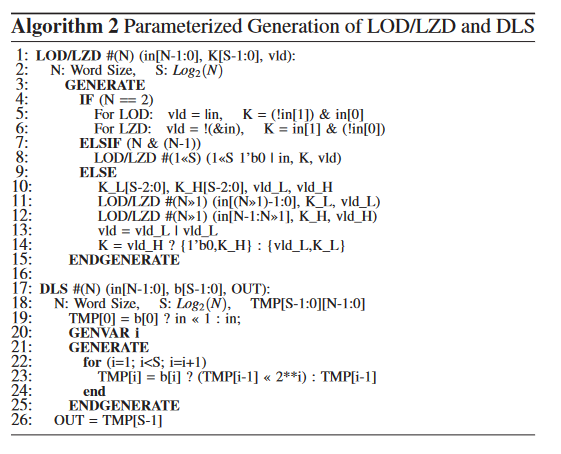
The components/statements in Algorithm-1 are presented with parameters N, E, ES and BIAS, and thus implemented, except LOD and dynamic shifters. The parameterized generation of LOD and LZD (leading zero detector, to be used in later units) are constructed in a similar hierarchical manner, except with a different respective basic 2:1 (LZD/LOD) building block (line 4-6), using parameterized Algorithm-2. For dynamic left/right shifting a parameterized barrel shifter is constructed with word width (N) and shifting amount (S) as parameter. A barrel shifter requires one N-bit 2:1 MUX for each bit of S. So, here it requires S numbers of 2:1 MUXs each of N-bit size. The parameterized generation for dynamic left shifter (DLS) is also shown in Algorithm-2, and similarly done for dynamic right shifter (DRS).

关键分析

1. 参数定义与功能

• N（字宽）：表示数据的总位数，例如32位或64位。
• E（指数部分）：可能用于浮点数格式中的指数位宽。
• ES（指数大小）：进一步明确指数部分的位数。
• BIAS（偏移量）：在浮点数中用于调整指数的表示范围（如IEEE 754中的偏移量）。
• LOD（Leading One Detector）：检测数据中最高有效位1的位置。
• LZD（Leading Zero Detector）：检测数据中前导零的数量。

2. LOD/LZD的层次化生成

• 基本模块：使用2:1的LZD/LOD单元作为基础模块。
  • LZD 2:1模块：检测两位输入中的前导零数量（例如输入01，输出为1）。
  • LOD 2:1模块：检测两位输入中的前导一位置（例如输入10，输出为1）。
• 分层构建：
  通过递归或分治策略，将大位宽的检测任务分解为更小的子模块。
  示例（8位LZD）：
  • 将8位分为高4位和低4位。
  • 若高4位全零，则LZD结果为低4位的LZD值 + 4。
  • 否则直接取高4位的LZD值。
• Algorithm-2的作用：定义如何递归组合这些子模块，生成任意位宽的LOD/LZD。

3. 动态移位器（DLS/DRS）的实现

• 桶形移位器结构：
  • 移位量（S）：表示需要移位的位数，例如S=3表示最多可移位7位（二进制111）。
  • 多路复用器（MUX）级联：
    • 每个MUX对应移位量的一个二进制位。
    • 例如S=3位：
      • 第1级MUX：处理移位量的最低位（1位左移或右移）。
      • 第2级MUX：处理次低位（2位左移或右移）。
      • 第3级MUX：处理最高位（4位左移或右移）。
  • 总资源消耗：需S个N位2:1 MUX，总逻辑门数为S × N。
• 动态左移器（DLS）：
  通过Algorithm-2生成，根据移位量的每一位控制MUX选择是否移位对应的2^k位。
• 动态右移器（DRS）：
  实现方式类似左移，但移位方向相反，可能需额外符号扩展或零填充逻辑。

4. Algorithm-2的通用性

• 参数化生成：
  Algorithm-2作为核心生成算法，支持不同位宽（N）和移位量（S）的配置。
• 代码示例（伪代码）：

  // Algorithm-2: 动态左移器生成
  module DynamicLeftShifter #(parameter N=32, S=5) (
      input [N-1:0] data_in,
      input [S-1:0] shift_amount,
      output [N-1:0] data_out
  );
      wire [N-1:0] stage [0:S];
      assign stage[0] = data_in;
      generate
          for (genvar i=0; i<S; i++) begin
              // 每级MUX处理移位量的第i位（2^i位移）
              assign stage[i+1] = shift_amount[i] ? 
                  {stage[i][N-1-2**i:0], {2**i{1'b0}}} : // 左移2^i位
                  stage[i];
          end
      endgenerate
      assign data_out = stage[S];
  endmodule
  

5. 资源与性能权衡

• 优势：
  • 灵活性：支持任意移位量和字宽配置。
  • 速度：桶形移位器通过多级MUX实现并行移位，延迟与移位量位数（S）成线性关系。
• 劣势：
  • 面积开销：移位量位数（S）越大，所需MUX数量越多，面积成本显著增加。
  • 关键路径：多级MUX级联可能导致时序紧张，需优化布局布线。

---

总结

• 核心设计思想：通过参数化（N, S）和分层递归（Algorithm-2）实现可配置的LOD/LZD及动态移位器。
• 关键技术点：
  1. LOD/LZD的层次化生成：利用2:1基本模块递归构建，适应不同位宽需求。
  2. 桶形移位器的多级MUX结构：通过移位量的二进制分解，逐级实现高效移位。
  3. Algorithm-2的通用性：作为生成算法，统一支持多种模块的参数化构建。
• 应用场景：适用于需要高灵活性的硬件设计（如浮点运算单元、可配置DSP核）。

代码分析与解释

1. LOD/LZD 的参数化生成

• 功能：递归生成前导一检测器（LOD）或前导零检测器（LZD），支持任意位宽 N（需为 2 的幂）。

• 参数：

  • N：输入数据位宽（例如 8、16）。
  • S = log2(N)：移位控制信号的位数。
  • in[N-1:0]：输入数据。
  • K[S-1:0]：输出前导位的位置（二进制编码）。
  • vid：有效标志（检测到有效前导位时为 1）。

• 逻辑分层：

  1. 基础情况（N=2）：
     • LOD：检测两位输入中的前导一位置。

       vid = in[1] | in[0];        // 至少有一位为 1
       K = in[1] ? 1'b1 : 1'b0;    // 高位为 1 则位置为 1，否则为 0
       

     • LZD：检测两位输入中的前导零数量。

       vid = !(in[1] & in[0]);     // 非全 1 时有效
       K = in[1] ? 1'b0 : 1'b1;    // 高位为 0 则位置为 1，否则为 0
       

  2. 递归拆分（N 是 2 的幂）：
     • 将输入分为高半部分（in[N-1:Ns]）和低半部分（in[Ns-1:0]），其中 Ns = N/2。
     • 递归生成子模块：

       LOD/LZD #(Ns) (in_low, K_L, vid_L);  // 处理低半部分
       LOD/LZD #(Ns) (in_high, K_H, vid_H); // 处理高半部分
       

     • 结果合并：
       • 若高半部分有效（vid_H=1），则最终位置为 K_H + Ns。
       • 若仅低半部分有效（vid_L=1），则最终位置为 K_L。

       vid = vid_H | vid_L;
       K = vid_H ? {1'b0, K_H} : {1'b1, K_L}; // 高位有效时忽略低位
       

---

2. 动态左移器（DLS）的参数化生成

• 功能：根据移位控制信号 b[S-1:0]，对输入数据 in[N-1:0] 进行左移操作，支持最大移位量 N-1。

• 参数：

  • N：数据位宽。
  • S = log2(N)：移位控制信号的位数。
  • b[S-1:0]：二进制编码的移位量（例如 b=3 表示左移 3 位）。
  • OUT[N-1:0]：移位后的输出。

• 实现逻辑：

  1. 分阶段移位：
     • 移位量 b 的每一位控制一级移位操作。
     • 第 i 级移位量为 2^i，由 b[i] 决定是否执行。
  2. 临时变量 TMP：
     • TMP[i] 存储第 i 级移位后的结果。
     • 初始值 TMP[0] = (b[0] ? in << 1 : in)，处理最低位移位。
  3. 循环生成移位级：

     generate
       for (i=1; i<S; i=i+1) begin
         // 第 i 级移位：若 b[i]=1，则左移 2^i 位
         TMP[i] = b[i] ? (TMP[i-1] << (1 << i)) : TMP[i-1];
       end
     endgenerate
     

  4. 最终输出：

     OUT = TMP[S-1];
     

---

关键修正与优化建议

1. DLS 移位量修正：

   • 原始代码中 << 2*** 应为 << (1 << i)，即左移 2^i 位。
   • 修正后：

     TMP[i] = b[i] ? (TMP[i-1] << (1 << i)) : TMP[i-1];
     

2. 非 2 的幂次方处理：

   • 当前代码假设 N 是 2 的幂，若需支持任意位宽，需添加填充逻辑（例如补零）。

3. LOD/LZD 结果合并逻辑：

   • 原始代码中 vid = vid_L | vid_L 应为 vid = vid_L | vid_H。
   • 修正后：

     vid = vid_L | vid_H;
     

---

示例验证

场景：8 位 LZD 检测

• 输入：in = 8'b0001_1100（前导零数量为 3）。
• 递归拆分：
  1. 第一层：拆分为高 4 位 0001 和低 4 位 1100。
  2. 高 4 位：继续拆分为 00 和 01，检测到前导零数量为 2。
  3. 低 4 位：拆分为 11 和 00，检测到前导零数量为 0。
• 合并结果：高位有效（前导零更多），最终 K = 2 + 2 = 4（二进制 100）。

场景：动态左移 3 位（N=8, b=3'b011）

1. 移位阶段：
   • TMP[0] = in << 1（移位 1 位）。
   • TMP[1] = TMP[0] << 2（再移位 2 位，累计 3 位）。
2. 输出：OUT = in << 3。

---

总结

• 设计优点：
  • 递归分治策略简化了复杂检测逻辑的实现。
  • 参数化生成支持灵活配置，适应不同位宽需求。
• 改进方向：
  • 支持非 2 的幂次方位宽。
  • 优化时序路径，减少多级 MUX 的延迟。
• 应用场景：浮点数规格化、优先级编码器、可配置 DSP 核等。

以下是对这篇关于 “Proposed Posit to FP Converter Flow” 算法文章的分析：

算法概述

• 该算法旨在实现一种从 Posit 数值格式到浮点数（FP）格式的转换流程，为在不同数值表示体系间进行数据转换提供了方法，有助于解决在不同计算环境或系统中数值表示差异所带来的兼容性问题。

算法细节

• 输入与初始化 ：给定参数 N、ES、E、BIAS 等，输入操作数 IN。然后进行 Posit 数据提取，包括符号位 Sp、Regime R、指数 Ep、尾数 Mp 以及异常情况 Infinity（INFP）和 Zero（Zp）的判断与初始化。
• 数据转换与处理 ：通过判断 IN 各位情况确定 Zp 和 INFP。依据 IN 的最高有效位（MSB）确定符号位 Sp。将输入 IN 转换为有符号数 XIN。进行 Regime 检查，确定 RC，并计算出 K0 以及 K1（对于正 Regime 序列）。计算绝对 Regime 值 R。确定 Regime 左移量 Lshift，根据 Lshift 对 XIN 进行动态左移得到 XIN tmp。从 XIN tmp 中提取指数部分 Ep 和尾数部分 Mp。
• 浮点数构造 ：根据 RC 等情况确定最终的指数部分 E0。处理特殊情况，如 INFP 和 Zp 情况下 FP0 的赋值，其他情况则按照常规的符号位、指数部分和尾数部分组合构造 FP0。

优势与意义

• 功能性 ：完整且系统地规定了从 Posit 到 FP 转换的各个步骤，涵盖了不同情况下的处理方式，能够准确地实现数值在两种格式间的转换，为相关数值计算和数据处理任务提供了有力支持。
• 通用性 ：给定参数 N、ES、E、BIAS 等可根据具体需求进行设定，适用于不同精度和范围要求的 Posit 和 FP 转换场景，具有较广泛的适用性。
• 规范性 ：以伪代码形式清晰地呈现了算法流程，便于研究人员、工程师等在实际的硬件设计、软件开发以及数值计算应用中进行参考、理解和实现，有助于规范和统一 Posit 到 FP 转换的操作流程。

局限性与改进方向

• 复杂性 ：算法涉及多个步骤和判断条件，对于一些对实时性要求较高的应用，可能需要进一步优化以提高转换效率。
• 精度控制 ：在转换过程中，可能会出现一定的精度损失，尤其是在处理特殊数值或进行尾数截断等情况时，需要进一步研究如何更好地控制和减少精度误差。
• 特定实现依赖性 ：该算法的实现可能依赖于特定的硬件架构或软件环境，对于不同的计算平台，可能需要进行相应的调整和优化以确保其正确性和性能。

1. XIN[N-2] acts as regime check bit (RC), which determines if it contains sequence of 0 or 1 (line 8). 2) To count a sequence of 0 with a terminating 1 (-ve regime) a LOD is applied for XIN[N-2:0]. Similarly, to count sequence on 1 with a terminating 0 (+ve regime) a LZD is applied for X[N-3:0] (1-bit less, as regime value would be one less than actual count of 1’s). 3) Based on RC, effective absolute regime value R (K0 or K1) (line 11), and regime left shift amount Lshift (line 12) are determined. 4) In order to extract the exponent and mantissa, the XIN is require to dynamically left shift so as to through-out the entire regime sequence and align exponent and mantissa at MSB. XIN_tmp is obtained by dynamic left shifting of XIN[N-3:0] (line 13). 5) Here, MSB ES bits of XIN_tmp are the exponent-bit and remaining bits are the mantissa (appending hidden bit at its MSB) (line 14-15).

以下是对这段关于 Posit 到浮点数（FP）转换算法关键点的分析：

关键点分析

1. Regime 检查与确定

   • XIN[N-2] 作为 Regime 检查位（RC），用于判断 regime 序列是 0 还是 1 ，这是确定后续处理流程的重要依据，为后续正确计算 regime 相关参数奠定基础。

2. LOD 与 LZD 应用

   • 对于负 regime 情况，使用 LOD（Leading One Detector）来计算 XIN[N-2:0] 中以 0 开头的序列长度，直到遇到终止的 1。对于正 regime 情况，使用 LZD（Leading Zero Detector）来计算 XIN[N-3:0] 中以 1 开头的序列长度，终止于 0，并且这里只计算到 XIN[N-3:0]（比实际可能的 regime 长度少 1 位），因为 regime 值会比实际 1 的个数少 1，这种处理方式准确地对应了不同 regime 类型下的序列特征，能够有效地确定 regime 的长度信息，进而影响指数部分的计算。

3. R 和 Lshift 确定

   • 根据 RC 来确定有效的绝对 regime 值 R，R 可能是 K0（对于负 regime 情况下的 LOD 结果）或 K1（对于正 regime 情况下的 LZD 结果加 1）。同时，Regime 左移量 Lshift 也是基于 RC 来确定，对于正 regime 情况，Lshift 是 K1 + 1，否则为 K0，这些参数将直接用于后续对 XIN 进行处理以提取指数和尾数，确保数据能够正确对齐和转换。

4. XIN 动态左移

   • 为了提取指数和尾数，需要将 XIN 动态左移，目的是去除整个 regime 序列，并将指数和尾数部分对齐到最高有效位（MSB）。通过将 XIN[N-3:0] 动态左移 Lshift 位得到 XIN tmp，从而为后续准确提取指数和尾数做好准备，这个过程是实现 Posit 到 FP 转换的关键步骤之一，确保数据在转换后的格式中能够正确表示数值的大小和精度。

5. 指数和尾数提取

   • 在 XIN tmp 中，前 ES 位（MSB 部分）作为指数位，剩余的位作为尾数，并且在尾数的 MSB 位置附加一个隐藏位。这一步骤完成了从 Posit 格式到 FP 格式指数和尾数部分的转换，是构建最终 FP 表示的核心环节，使得转换后的浮点数能够准确反映原 Posit 数的数值信息。

The proposed parameterized algorithmic flow for posit addition is shown in algorithm-4. The major blocks in this include Posit Data Extraction, Core Adder Arithmetic Processing, Data Composition and Post-Processing. This same computation flow can be used for posit subtraction also, after negating the second operand. Similar to posit data extraction in Algorithm-3, data extraction is performed on both operands IN1, IN2 (line 6-8). The core arithmetic stage involves the mantissa addition, and final exponent and regime numerical value computation. This follows from line 10 to 28. These processing are mostly analogous to FP standard except regime inclusion. First effective operation is evaluated. A comparison of XIN1 and XIN2 gives the information of large and small operand, and large/small components are thus evaluated. A decimal point alignment of both mantissa is achieved by dynamic right shifting of smaller mantissa by Ediff (the difference of effective large exponent and small exponent, by combining R and E). Based on the effective operation OP, the small shifted mantissa is added/subtracted from large mantissa LM by using a N-bit add/sub unit, and result is checked for mantissa overflow and underflow (which requires left/right shifting). The total effective large exponent (Exp) is computed (line 27) by combining LRC, LR, Movf, and Nshift. Further, similar to line 18-26 of FP to Posit converter Algorithm-1, the EO and RO are computed. The regime, exponent and mantissa packing is done similar to the (line 27-29 of Algorithm-1) FP to posit converter procedure. At this stage, rounding operation is performed. The final REM is then combined by the large sign bit (LS) to produce the posit addition result, while considering ZERO and Infinity check of the input operands.

以下是对这段关于 posit 加法算法描述的分析：

算法概述

• 这段描述展示了算法 4 中提出的参数化 posit 加法算法流程，该流程包含几个主要模块，包括 Posit 数据提取、核心加法算术处理、数据组合和后处理。此外，该计算流程也可用于 posit 减法，只需对第二个操作数进行取反操作。

关键步骤分析

1. 数据提取

   • 类似于算法 3 中的 Posit 数据提取，对两个操作数 IN1 和 IN2 执行数据提取操作（第 6-8 行）。这一步骤是后续算术运算的基础，通过提取操作数的各项信息（如符号、指数、尾数、regime 等），为后续准确地进行数值计算提供数据支持。

2. 核心算术处理

   • 主要包括尾数加法以及最终的指数和 regime 数值计算（第 10-28 行）。这一阶段的处理与浮点数（FP）标准类似，但包含了 regime 相关的处理。
   • 首先评估第一个有效的操作。通过比较 XIN1 和 XIN2 确定较大和较小的操作数，并分别计算出较大的和较小的组成部分。这有助于确定哪个操作数的指数较大，从而在后续的尾数对齐中起主导作用。
   • 为实现两个尾数的小数点对齐，通过动态右移较小的尾数来达到对齐目的，右移的位数由 Ediff 决定。Ediff 是通过结合 regime（R）和指数（E）计算出的有效较大指数与较小指数之差。这种动态右移操作确保了尾数在加减法运算中的对齐，为准确计算结果提供了保障。
   • 根据有效的操作 OP，利用 N 位加/减单元对较小的移位尾数进行加或减操作，得到结果后检查尾数是否溢出或下溢，这涉及到左移或右移操作以调整结果。
   • 计算出总的有效较大指数（Exp）（第 27 行），该指数是通过综合 LRC、LR、Movf 和 Nshift 等因素得到的。这一步骤确保了指数能够准确反映加减法运算后的数值规模。
   • 此外，与算法 1 的 FP 到 Posit 转换器中第 18-26 行类似，计算 EO 和 RO。接着，类似于算法 1 中第 27-29 行 FP 到 Posit 转换的程序，进行 regime、指数和尾数的打包操作。在这一阶段，还会执行舍入操作，以确保结果的精度符合要求。
   • 最后，将较大的符号位（LS）与经过处理的尾数、指数等组合在一起，生成最终的 posit 加法结果，同时考虑输入操作数的零和无穷大检查，以确保结果的正确性和合理性。

优势与意义

• 通用性 ：该算法不仅可以用于 posit 加法，还可以通过简单的操作扩展用于 posit 减法，提高了算法的适用范围和灵活性。
• 与 FP 标准的兼容性 ：核心算术处理阶段的大部分操作与浮点数（FP）标准类似，这意味着该算法可以在一定程度上借鉴和利用现有的 FP 计算架构和方法，降低了实现难度和成本。
• 精确性和灵活性 ：通过动态右移等操作实现尾数对齐，以及对指数和 regime 的综合计算，能够精确地处理不同规模的 posit 数之间的加减法运算，同时，参数化的设计使得算法可以根据不同的数值范围和精度要求进行调整和优化。

局限性与改进方向

• 复杂性 ：由于涉及多个步骤和多个因素的综合计算，该算法相对复杂，对于硬件实现来说，可能需要较高的硬件资源和较复杂的控制逻辑，这可能会影响运算速度和效率。
• 精度控制 ：在舍入操作和尾数溢出/下溢处理过程中，可能会存在一定的精度损失，如何更好地控制和减少精度误差是该算法需要进一步研究和改进的方向。
• 特殊情况处理 ：对于零和无穷大的检查虽然在算法中有所考虑，但在实际应用中，还需要进一步完善对各种特殊情况（如 NaN 等）的处理，以确保算法的鲁棒性和可靠性。

Basically, in the core of posit multiplier unit it requires to multiply both mantissas and sum their effective exponents. The proposed algorithmic flow for posit multiplier is shown in algorithm-5. Most components and their descriptions in this unit are similar to the Adder arithmetic flow. Line 3-6 extract data same as adder unit. Line 7 determined the actual (+ve / -ve) of regime (RG1 and RG2) using respective regime check bits (RC1 and RC2), to be used for operands exponent sum processing. The mantissa multiplication processing is performed on lines 8-11, where both mantissas are multiplied using integer multiplier, which result later checked for overflow and then shifted by 1-bit accordingly. The exponent sum is performed at line 13 which sums up effective exponents (by combing regime and exponent-bits) of both operands. All the remaining processing goes similar to the posit adder unit.
以下是对这段关于 posit 乘法器算法描述的分析：

算法概述

该段描述阐述了 posit 乘法器算法的核心流程，即主要涉及尾数相乘和有效指数相加的操作。算法 5 展示了该算法流程，其大部分组件及其描述与加法器算术流程相似。

关键步骤分析

1. 数据提取

   • 算法的第 3-6 行进行数据提取操作，与加法器单元相同。这一步骤从输入的操作数中提取出所需的各种信息，为后续的乘法运算做准备。

2. Regime 实际正负确定

   • 第 7 行通过各自的 regime 检查位（RC1 和 RC2）来确定 regime（RG1 和 RG2）的实际正负情况。这一步骤对于操作数的指数求和处理至关重要，因为 regime 的正负会影响指数的计算。

3. 尾数乘法处理

   • 第 8-11 行执行尾数乘法处理。使用整数乘法器对两个尾数进行相乘操作，之后检查结果是否溢出，并根据检查结果进行相应的 1 位移位调整。这一步骤确保了尾数乘法结果的正确性和合理性，同时溢出检查和移位操作有助于后续对结果进行归一化处理。

4. 指数求和

   • 第 13 行进行指数求和操作，将两个操作数的有效指数（通过结合 regime 和指数位计算得到）相加。这一步骤得出了乘法结果的指数部分，该指数与尾数乘法结果共同决定了最终的乘法结果的数值大小。

5. 后续处理

   • 除上述步骤外，posit 乘法器的其余处理流程与 posit 加法器单元类似。包括数据的组合、归一化、舍入等操作，这些步骤确保了乘法结果能够以正确的 posit 格式表示，并且满足精度和数值范围的要求。

特点分析

1. 与加法器的相似性

   • posit 乘法器算法在许多方面与加法器算法相似，如数据提取步骤、后续处理流程等。这表明两种算法在结构和思路上有一定的共通性，有助于在实现过程中借鉴和共享部分方法和组件。

2. 关键操作的差异性

   • 尽管存在相似之处，但乘法器算法的核心在于尾数相乘和指数相加，这与加法器中的尾数加减和指数处理有所不同。这种差异体现了两种运算在数值处理上的本质区别，也决定了乘法器算法在尾数乘法和指数求和方面的独特处理方式。

3. 简洁性与高效性

   • 该算法描述简洁明了，突出了 posit 乘法器的关键操作步骤。通过合理利用整数乘法器和相应的溢出检查与移位操作，能够高效地完成尾数乘法运算，并结合指数求和得到最终结果。

总结

这段描述清晰地展示了 posit 乘法器算法的核心流程和关键步骤，强调了其与加法器算法的相似性和差异性。通过尾数相乘、指数求和以及后续的处理操作，该算法能够准确地实现 posit 数的乘法运算，为 posit 数在各种数值计算应用中的使用提供了基础支持。

图片中展示了算法5：一种 Posit 乘法器的计算流程，用于实现 Posit 数的乘法运算。以下是对图片内容的解释：

输入和初始化

• 输入参数：N（Posit 的字长）、ES（Posit 指数字段大小）、RS（Posit regime 值存储空间位数），类似于算法4中的定义。
• 输入操作数：两个 Posit 数 IN1 和 IN2。

数据提取

• 数据提取过程：类似于算法3和算法4中的数据提取步骤，从 IN1 和 IN2 中提取出有效的操作数（XIN1 和 XIN2），以及符号位（S1 和 S2）、Regime 检查位（RC1 和 RC2）、指数（E1 和 E2）、尾数（M1 和 M2）等信息。
• Zero 和 Infinity 检查：如果 IN1 或 IN2 是 Zero，则 Z 被设置为 1；如果任一操作数是 Infinity，则 Inf 被设置为 1。

核心算术处理

• Regime 实际正负确定：
  • 根据 Regime 检查位（RC1 和 RC2）确定 regime RG1 和 RG2 的正负值。如果 RC1 为真，则 RG1 是 R1，否则 RG1 是 -R1；同理，RG2 的确定方式类似。
• 尾数乘法处理：
  • 使用整数乘法器将两个尾数 M1 和 M2 相乘，得到乘积 M。
  • 检查乘积 M 是否溢出（通过查看最高有效位）。如果溢出，则将 M 右移一位。
  • 将结果尾数 M 左移一位（如果是非溢出情况），以调整结果。
• 指数求和：
  • 计算最终的指数 E0 和 regime R0，通过结合操作数的 regime 和指数信息，以及尾数乘法后的溢出情况。

数据组合、舍入和最终输出

• 数据组合：将处理后的尾数、指数和 regime 组合起来，形成最终的 Posit 结果。
• 舍入操作：采用舍入到零（截断）的方式。
• 最终输出：结合符号位 LS 和舍入后的结果，生成最终的 Posit 乘法结果，同时考虑输入操作数的 Zero 和 Infinity 检查。

总结

该算法展示了 Posit 乘法器的计算流程，其核心是尾数相乘和指数求和操作。通过合理使用整数乘法器和相应的移位操作，能够准确地实现 Posit 数的乘法运算，同时算法在结构上与加法器算法具有一定的相似性，有助于在实现过程中共享部分方法和组件。