热辐射

1. 热辐射的基本概念

1.1 热辐射的产生

热辐射讨论的是位于0.1~100 \(\mu m\) 范围内的电磁波波段，因为这一波长区段内的电磁波最容易被物体吸收并转化为热能。

辐射是电磁波传递能量的现象，由于热的原因而产生的电磁波辐射称为热辐射（Thermal Radiation），热辐射的电磁波是物体内部微观粒子的热运动状态改变时激发出来的，只要物体的温度高于绝对零度就会持续向外部发出热辐射，同时物体也在不断地吸收来自外部的热辐射，并把吸收的辐射能转换成热能。

辐射换热就是指物体之间相互辐射和吸收的总效果，当物体与环境处于热*衡时，其表面的热辐射仍在持续进行，但其净辐射传热量等于零。

1.2 与导热、对流换热的区别

基于辐射是电磁波的传递这一事实，其与导热、对流换热的主要区别如下：

热辐射能量的传递不需要任何介质，并且在真空中传递效率最高；
在物体发射和吸收辐射能量的过程中发生了电磁能和热能两种能量形式的转换。

1.3 从电磁波的角度描述热辐射特性

1.3.1 电磁波的传播速率

热辐射具有一般辐射现象的共性，与电磁波的传播相同，电磁波的速率、波长和频率存在如下关系：

\[c = f \lambda \tag{1} \]

式中：\(c\) = 电磁波传播速率，在真空中等于光速，即 \(c = 3 \times 10^8 \; m/s\)大气中略低于此值；
\(f\) = 频率，\(s^{-1}\)；
\(\lambda\) = 波长，单位为 \(m\)，常用单位为 \(\mu m\)。

1.3.2 电磁波波谱

如图所示为电磁波波谱：

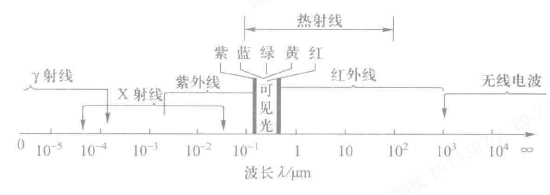
2000K(1706.85 ℃) 以下——有实际意义的热辐射波长位于 0.8~100 \(\mu m\) 之间，且大部分能量位于红外线区段的 0.76~20 \(\mu m\) 范围内，而在可见光区段，即波长位于 0.38~0.76 \(\mu m\) 范围内，热辐射的能量比重不大。热辐射波长大于0.76 \(\mu m\)时，肉眼将不可见。

对于太阳辐射，即 5800K 的热源，辐射能量主要集中在 0.2~3 \(\mu m\) 的波长范围，其中可见光区段占很大比重。因此如果把太阳辐射包含在内，热辐射的波长区段可放宽为 0.1~100 \(\mu m\)。

1.3.3 物体表面对电磁波作用

（1）吸收比、反射比与穿透比

热辐射的能量投射到物体表面上时，和可见光一样，也发生吸收、反射和穿透现象。外界投射到物体表面的总能量 \(Q\) 中，包含物体吸收的能量 \(Q_{\alpha}\) 、从物体表面反射出的能量 \(Q_{\rho}\) 、穿透物体的能量 \(Q_{\tau}\)，如图所示，

\[Q = Q_{\alpha} + Q_{\rho} + Q_{\tau} \]

\[\frac{Q_{\alpha}}{Q} + \frac{Q_{\rho}}{Q} + \frac{Q_{\tau}}{Q} = 1 \]

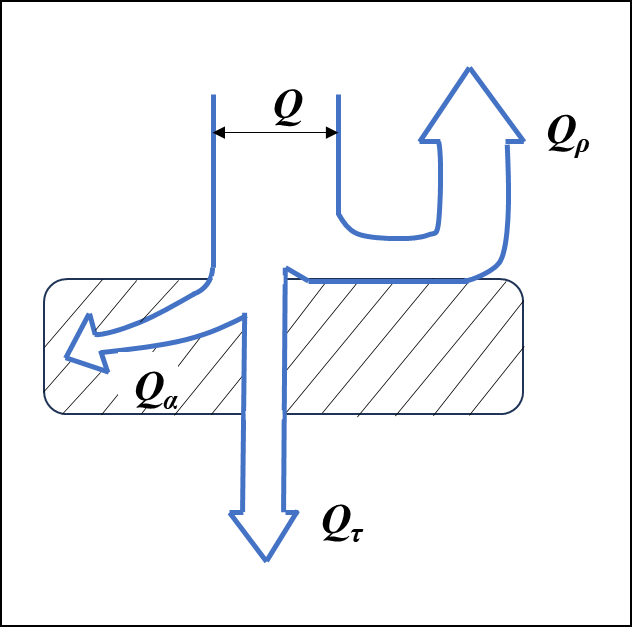
式中：\(\frac{Q_{\alpha}}{Q}\) = 吸收比（吸收率）；\(\frac{Q_{\rho}}{Q}\) = 反射比（反射率）；\(\frac{Q_{\alpha}}{Q}\) = 穿透比（穿透率）。分别记为 \(\alpha\) 、\(\rho\)、\(\tau\)，即：

\[ \alpha + \rho + \tau = 1 \]

对于固体和液体，对热辐射可以认为只存在吸收和反射，因为在辐射能进入固体或者液体介质1微米的数量级之后就会被吸收完全，实际的工程材料厚度一般都大于该值，因此对于固体和液体：

\[\alpha + \rho = 1 \]

对于透明的玻璃，如何理解辐射能只存在吸收和反射，而不存在穿透，对于阳光透过玻璃仍然感觉到暖和的现象如何解释？
答：玻璃的“透明”是指可见光的透过性，不同玻璃的材料对不同波长的可见光的透过性不同。太阳光的热辐射主要集中在0.2~3\(\mu m\) 波长范围内，包含可见光、红外线（*红外），玻璃可以透过可见光，并且太阳光的辐射能波段包含可见光波段，因此这些透过的可见光可以感觉到暖和。
而对于一般的物体辐射能，能量远低于太阳光，比如上面所描述低于2000K时，主要辐射能量波段位于红外波段 0.76~20 \(\mu m\) ，可见光波段的辐射能可忽略不计，玻璃对可见光有透过性，因此不存在可见光的辐射波段，红外波段的辐射能无法透过玻璃，认为只存在吸收和反射。

对于气体，气体的辐射能几乎没有反射能力，因此反射率为0：

\[\alpha + \tau = 1 \]

拓展：

红外辐射包含*红外辐射和远红外辐射，*红外与远红外以 25\(\mu m\) 为界，小于该值为*红外，大于该值为远红外。
波长在1mm~1m之间的电磁波称为微波（Microwave），位于该区段的电磁波可以穿过塑料、玻璃以及陶瓷制品，但是会被向水那样具有极性的分子所吸收，在物体内部产生内热源，进而实现均匀加热。
波长>1m的电磁波广泛应用于无线电技术中。

（2）固体表面的两种反射

辐射能投射到固体表面后的反射现象和可见光一样，有镜面反射和漫反射。取决于表面粗糙程度，这里的粗糙程度是相对于热辐射的波长大小而言的。

当固体表面不*整尺寸小于入射辐射波长时，形成镜面反射；
当固体表面不*整尺寸大于入射辐射波长时，形成漫反射。

大部分的固体表面都会形成漫反射，对于高度磨光的金属板就是镜面反射。

2. 黑体热辐射定律

2.1 黑体辐射模型

为了研究方便，需要引入对应的理想模型：

吸收比\(\alpha\) = 1 的物体称为黑体模型；
反射比\(\rho\) = 1 的物体称为镜体模型，漫反射时为白体；
穿透比\(\tau\) = 1 的物体称为绝对透明体模型。

黑体模型：选用吸收比较大的材料制造一个空腔，在空腔壁面开个小孔，设法保证空腔内壁保持均匀的温度，此时空腔上的小孔就有黑体辐射的特性。这是因为入射辐射能通过小孔进入空腔内，由于内壁表面对辐射能的吸收率比较大，因此仅存在极小比例的辐射能在壁面表面发生反射，由于是球型腔体，辐射能在内部来回反射，最终经过小孔反射出去的辐射能占比已经微乎其微了。

对于制造空腔的材料本身的吸收比大小原则上对黑体模型没有影响，只是在一定的小孔面积与空腔内壁总表面积之比的情况下，材料本身的吸收比越大，黑体模型的有效吸收比就越大；小孔面积占空腔内壁总面积的份额越小，小孔吸收比就越高。

对于球型内壁面的黑体模型，若小孔面积占空腔内壁面总表面积小于0.6%，当内壁吸收比为0.6时，小孔的吸收比可大于0.996.

在这样的等温空腔内部，辐射是均匀且各向同性的，空腔内表面的辐射（指的是有效辐射，包括该表面的自身辐射以及反射的辐射在内）就是同温度下的黑体辐射。

引出黑体辐射模型的目的在于确定修正系数，来定量描述实际物体表面的辐射。

2.2 黑体辐射定律

黑体辐射定律有三大基本定律，分别从不同的角度揭示了在一定的温度下，单位表面黑体辐射能的多少以及 其随空间方向 与 随波长分布 的规律。

2.2.1 斯忒藩-玻尔兹曼（Stefan-Boltzmann）定律

引入辐射力的概念来描述黑体在一定温度下向外面的辐射量的大小。单位时间内单位表面积向其上的半球空间的所有方向辐射出去的全部波长范围内的能量称为辐射力（Emissive power），辐射力的单位为 \(W/m²\)。

黑体辐射力与热力学温度（K）的关系由 Stefan-Boltzmann 定律确定：

\[E_b = \sigma T^4 = C_0 \left(\frac{T}{100}\right)^4 \tag{2} \]

式中：\(\sigma\) 为黑体辐射常数，有\(\sigma = 5.67 \times 10^{-8} \; W/(m² \cdot K^4)\)；\(C_0\) 称为黑体辐射系数，其值为 \(5.67 \; W/(m² \cdot K^4)\)，角标 b 表示黑体。

该定律又称之为四次方定律，其表明辐射力的大小受温度的影响极大，随着温度的上升，辐射力急剧增加。

例：一黑体表面置于室温为27℃的厂房中，试求在热*衡条件下的黑体表面辐射力，如将黑体加热到327℃，它的辐射力又是多少？
解：根据 Stefan-Boltzmann 定律可知：

\(T =27 + 273.15 = 300.15 K\) 时，\(E_b = 5.67 \times (\frac{300.15}{100})^4 = 460 W/m²\)；
\(T =327 + 273.15 = 600.15 K\) 时，\(E_b = 5.67 \times (\frac{600.15}{100})^4 = 7355 W/m²\)
可知，温升300K情况下，虽然温度之比（开尔文）只有2倍，黑体辐射力之比为\(\frac{7355}{460} \approx 16\)，可见黑体辐射力大小随温度升高而急剧增大。

2.2.2 普朗克（Max Planck）定律

普朗克定律描述的是黑体辐射能按照波长分布的规律，为此引入光谱辐射力的概念，记为 \(E_{b \lambda}\)，单位为 \(W/(m² \cdot m)\) 或者 \(W/(m² \cdot \mu m)\)。这里分母位置的长度单位表示单位波长的宽度。

黑体的光谱辐射力随波长变化由普朗克定律所描述：

\[E_{b \lambda} = \frac{c_1 \lambda^{-5}}{e^{\frac{c_2}{\lambda T}}-1} \tag{3} \]

式中：
\(E_{b \lambda}\) = 黑体光谱辐射力，\(W/m³\)；
\(\lambda\) = 波长，\(m\)；
\(T\) = 黑体热力学温度，\(K\)；
\(c_1\) = 第一辐射常量，\(3.7419 \times 10^{-16} \; W \cdot m²\)；
\(c_2\) = 第二辐射常量，\(1.4388 \times 10^{-2} \; m \cdot K\).

从图示可以看出，黑体光谱辐射力随着波长的增加，先是增大，然后又减小。光谱辐射力最大处的波长 \(\lambda_m\) 亦随温度不同而变化。

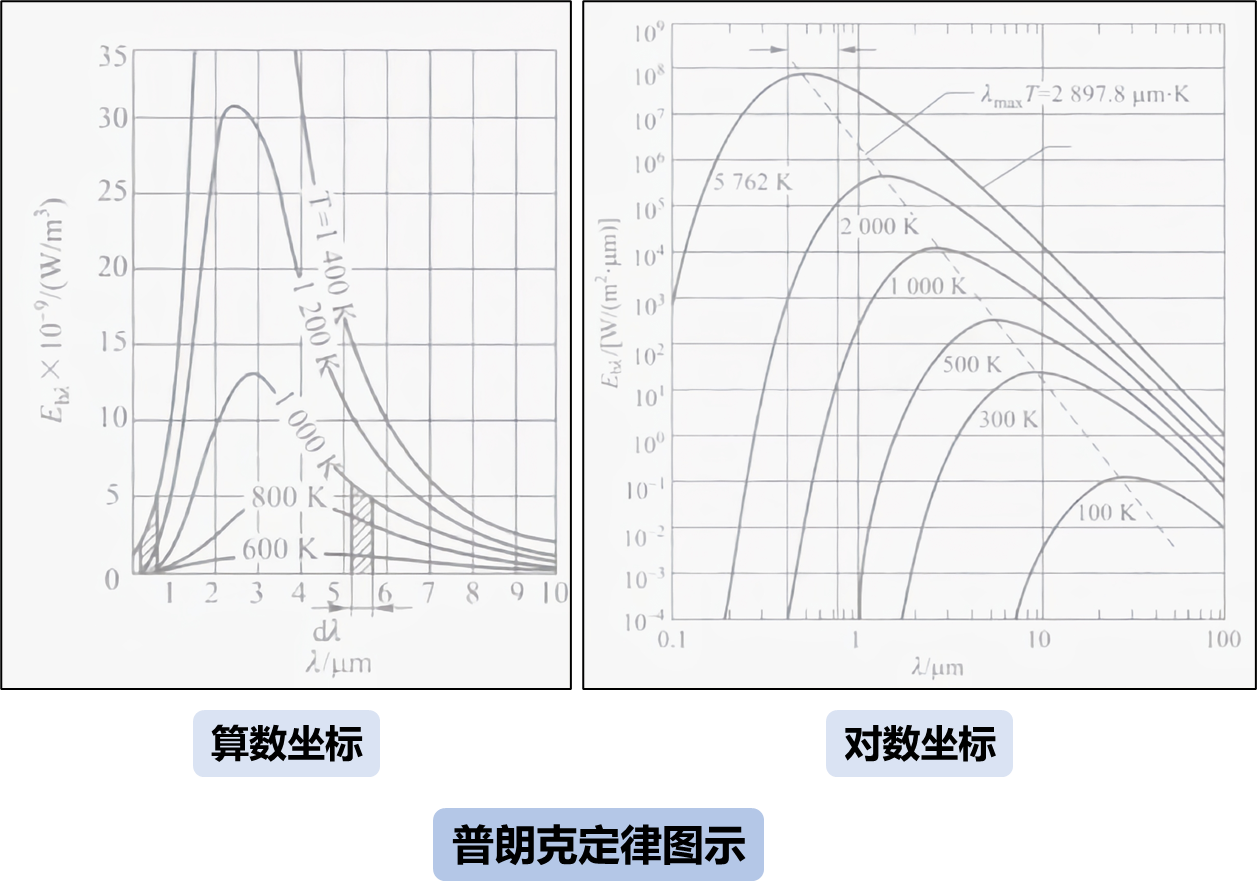
通过光谱辐射力曲线可以看出，随着温度的增高，曲线的峰值向左移动，即移向较短的波长，说明温度越高，波长较短的辐射力越强，波长越短，频率就越高。

维恩定律描述了这一现象：对应于最大辐射力的波长 \(\lambda_m\) 与温度 \(T\) 的乘积为定值：

\[\lambda_m T =2.8976 \times 10^{-3} \; m \cdot K \approx 2.9 \times 10^{-3} \; m \cdot K \tag{4} \]

上式的得出可以通过式3对 \(\lambda\) 进行求导并使其等于零而得出。

例：分别计算温度为2000K和5800K的黑体的最大单色辐射力所对应的波长\(\lambda_m\)
解：结合维恩定律有：

T = 2000K时，\(\lambda_m = \frac{2.8976 \times 10^{-3}}{2000} = 1.45 \mu m\)；
T = 5800K时，\(\lambda_m = \frac{2.8976 \times 10^{-3}}{5800} = 0.58 \mu m\)
对比电磁波波谱图可知，低于2000K的黑体最大单色辐射力所对应的波长位于红外波段（0.8-1000 \(\mu m\)），而温度约等于太阳表面温度的黑体最大单色辐射力所对应的辐射波长位于可见光波段（0.38-0.76 \(\mu m\)）.另外可知，黑体最大单色辐射力对应波段在可见光区段时的温度范围为 3813-7625K，位于红外区段的温度范围为 2.9-3622K.

再比如温度\(T =850 ℃ = 850+273.15 = 1123.15K\)，那么该温度下的黑体最大单色辐射力所对应的波长\(\lambda_m \approx 2.58 \mu m\) ，位于*红外波段。

上面所述得知，Stefan-Boltzmann 定律描述的是所有波段的光谱辐射力，而普朗克定律描述的是特定波段的光谱辐射力，光谱辐射力的曲线图中特定温度下的辐射力曲线与坐标轴所围成的面积就是所有波段的光谱辐射力

\[E_b = \int_0^\infin E_{b \lambda} d \lambda = \int_0^ \infin \frac{c_1 \lambda^{-5}}{e^{\frac{c_2}{\lambda T}}-1} d \lambda \tag{5} \]

那么特定波段 \(0~\lambda\) 范围内的黑体辐射能

\[E_{b(0-\lambda)} = \int_0^\lambda E_{b\lambda}d\lambda \tag{6} \]

其在黑体辐射力中所占的百分数为

\[F_{b(0-\lambda)} = \frac{\int_0^\lambda E_{b\lambda}d\lambda}{\sigma T^4} = \int_0^\lambda \frac{c_1 (\lambda T)^{-5}}{e^{\frac{c_2}{\lambda T}}-1} \frac{1}{\sigma} d(\lambda T) = f(\lambda T) \tag{7} \]

可见该式是关于 \(\lambda T\) 的函数，该式称为黑体辐射函数（block body radiation function），并且有相应的黑体辐射函数值查询表，根据这个表格可以计算：任意两个波长\(\lambda_2\)、\(\lambda_1\) 之间黑体的辐射能

\[E_{b(\lambda_1-\lambda_2)} = F_{b(\lambda_1 - \lambda_2)}E_b = \left( F_{b(0-\lambda_2)}-F_{b(0-\lambda_1)}\right)E_b \tag{8} \]

例：试分别计算温度为1000K、1400K、3000K以及6000K时可见光和红外线辐射在黑体总辐射中所占的份额。
解：已知可见光波段0.38-0.76\(\mu m\)，红外波段0.76-1000\(\mu m\)。各温度下的\(\lambda_m T\) 值如下表所示

\(T\)	\(\lambda_m = 0.38 \mu m\)	\(\lambda_m = 0.76 \mu m\)	\(\lambda_m = 1000 \mu m\)
1000	380	760	1000000
1400	532	1064	1400000
3000	1140	2280	3000000
6000	2280	4560	6000000

查表得各温度下特定波段的黑体总辐射占比为

\(T\)	\(F_{b(0-0.38)}\)	\(F_{b(0-0.76)}\)	\(F_{b(0-1000)}\)
1000	<0.03%	<0.03%	>99.99%
1400	<0.03%	≈0.03%	>99.99%
3000	0.09%	12%	>99.99%
6000	12%	57%	>99.99%

可见光波段、红外波段占比

\(T\)	\(F_{b(0.38-0.76)}\)	\(F_{b(0.76-1000)}\)
1000	<0.1%	>99.99%
1400	0.4%	99.96%
3000	11.01%	88.99%
6000	45%	55%

结论：T<1000K时的黑体辐射中可见光占比远不到千分之一，只有温度升高到3000K左右时的可见光比例才达到10%以上，这一关于可见光在物体自身辐射中的所占比例，总体上对大多数实际物体的辐射也适用。

2.2.3 兰贝特（Lambert）定律

兰贝特定律描述了黑体辐射能沿空间方向的分布规律，因此引入立体角的概念来表示空间方向以及大小。
（1）立体角
类似于空间中两*面的夹角，可以用三维空间的立体角（solid angle）以及微元立体角来表示某一方向的空间所占的大小。如下图所示表示微元立体角与半球空间几何参数之间的关系。

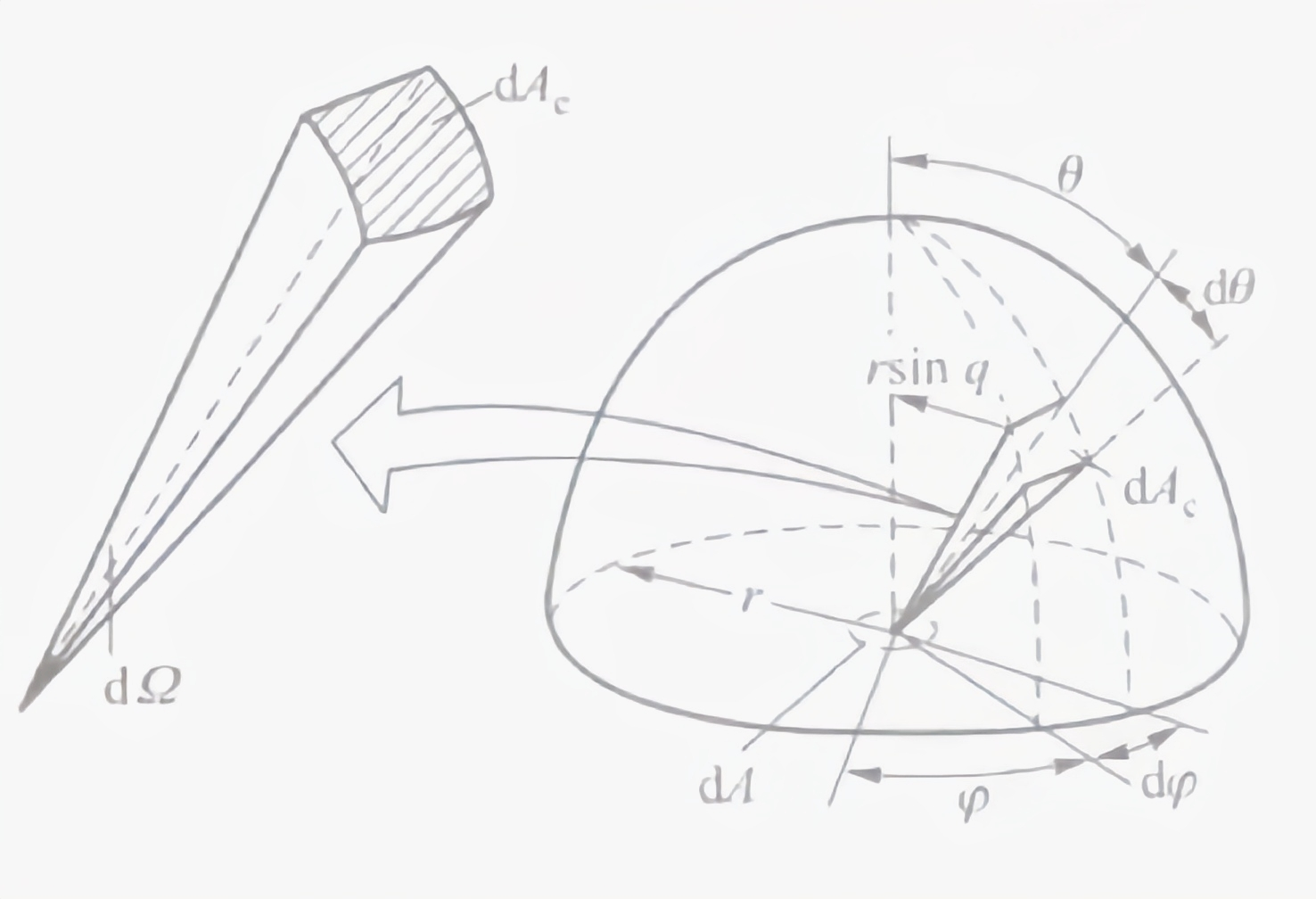
那么有：

\[\Omega = \frac{A_c}{r^2}，d\Omega = \frac{dA_c}{r^2} \tag{9} \]

在图示中的坐标系中，\(\varphi\) 为经度角（longitudinal angle），\(\theta\) 为纬度角。空间的方向可以通过这两个角度来表示，为了说明黑体向半球空间辐射出去的能量按不同方向分布的规律只有对不同方向的相等的立体角来对比才有意义，立体角的单位称为空间度，记为 \(sr\)。

<暂定，还不太理解>

（2）定向辐射强度

（3）兰贝特定律——余弦定律

3. 固体、液体、气体的辐射特性

3.1 固体和液体的辐射特性

黑体是研究辐射的理想模型，实际物体的辐射特性将在与黑体辐射特性进行对比的基础上来研究的。显然实际物体并不能像黑体那样能够完全吸收投射到其表面上的辐射能量。

3.1.1 实际物体的辐射力

由于实际物体的辐射力\(E\)总是小于同温度下的黑体辐射力\(E_b\)，定义两者之间的比值称为实际物体的发射率（Emissivity 或者Emittance，习惯上称为黑度），记为\(\varepsilon\)：

\[\varepsilon = \frac{E}{E_b} \]

因此实际物体的辐射力可以表示成：

\[E = \varepsilon E_b = \varepsilon \sigma T^4 = \varepsilon C_0 \left( \frac{T}{100} \right)^4 \tag{10} \]

习惯上，上式亦可称为四次方定律，物体的发射率一般通过实验获得，它仅取决于物体本身，而与周围环境条件无关。

3.1.2 实际物体的光谱辐射力

实际物体的光谱辐射力按波长分布的规律与普朗克定律不同，但定性上是一致的。实际物体的光谱辐射力小于同温度下的黑体同一波长下的光谱辐射力，两者之比称为实际物体的光谱发射率（Spectral Emissivity）：

\[\varepsilon = \frac{E_{\lambda}}{E_{b \lambda}} = \frac{\int_0^ \infin \varepsilon(\lambda) E_{b \lambda} d \lambda}{\sigma T^4} \tag{11} \]

实验结果发现，实际物体的辐射力并不严格正比于热力学温度的四次方，但为了使用方便，在工程计算中仍认为一切实际物体的辐射力与热力学温度的四次方成正比，而由此引起的修正包含在用实验方法确定的发射率中去，由于这个原因，发射率与温度有依变关系。

灰体是吸收比和光谱发射率与波长无关的物体。

3.1.3 实际物体的定向辐射强度

实际物体辐射按照空间方向的分布并不完全都符合兰贝特定律。这就说明实际物体的定向辐射强度在不同空间方向上是变化的，为了说明不同方向上定向辐射强度的变化，给出定向辐射（定向黑度）的定义：

\[\varepsilon(\theta) = \frac{I(\theta)}{I_b(\theta)} = \frac{I(\theta)}{I_b} \tag{12} \]

式中：\(I(\theta)\) 表示与辐射面法向成\(\theta\) 角的方向上的定向辐射强度，\(I_b\) 为同温度下黑体的定向辐射强度。

对于黑体来讲，定向发射率在极坐标中是半径为1的半圆，对于定向辐射强度满足兰贝特定律的物体，其定向反射率在极坐标中是半径小于1的半圆，这样的物体称为漫射体（Diffuse Body）。

对于非导电体：从辐射面法向0°-60°范围内，定向发射率基本不变，当\(\theta\) 超过60°后，\(\varepsilon(\theta)\) 的减小是明显的，直至\(\theta = 90°\) 时 \(\varepsilon(\theta)\) 降为0。
对于导电体：从\(\theta = 0°\) 开始，在一定角度范围内，\(\varepsilon(\theta)\) 可认为是一个常数，然后随着\(\theta\) 的增加而急剧增大，在接*\(\theta = 90°\) 的极小角度范围内 \(\varepsilon(\theta)\) 的值又减小直至为零。

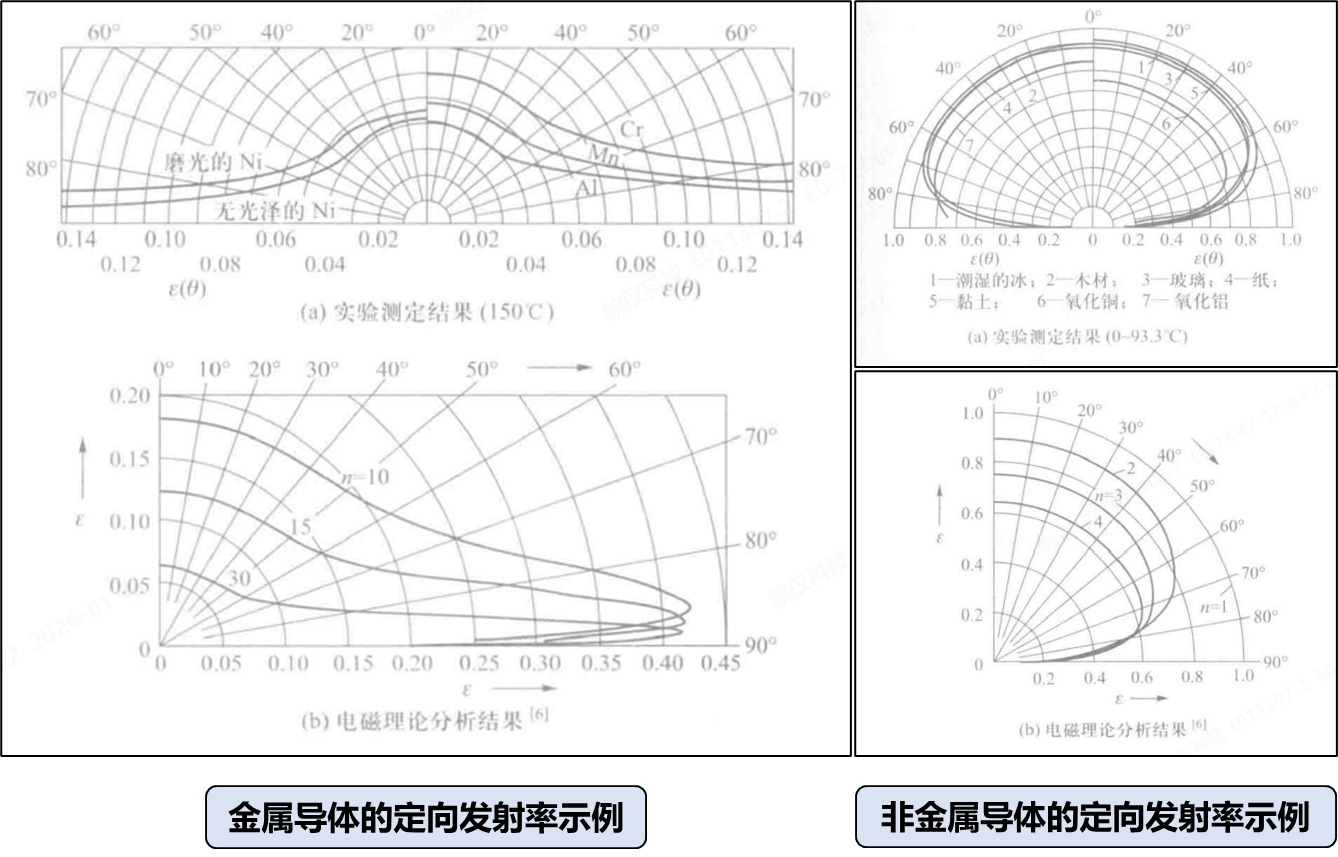
上面式10中定义的\(\varepsilon\) 是指在整个半球范围内的辐射能与黑体的辐射能量之比，为突出其与定向发射率的区别，这里特别增加了半球这一定语，根据上图可知，可以认为在半球空间的大部分范围内，不论是金属还是非金属，定向发射率基本是个常数，可用法向发射率来*似代替，于是实际物体辐射表面的发射率就有

\[\varepsilon = M \varepsilon_n \tag{13} \]

式中：\(M\) 为修正系数，除了高度磨光的表面以外，工程计算中一般取\(M = 1\)，即法向辐射率等于辐射表面发射率。

对于金属表面\(M =1 \sim 1.3\)（高度磨光的表面取上限）；对于非导体\(M =0.95 \sim 1\)（粗糙表面取上限）。

这一简化会带来两个结果：一般工程手册中给出的物体发射率常常是法向发射率，而在计算高度磨光的物体表面时需考虑实际发射率与法向发射率的误差；另外，既然大部分工程材料的定向发射率可以*似为常数，而不存在各异性，那么就可以将它们作为漫射体。下面讨论的物体表面间的辐射传热都是将它们视为漫射体来处理。

物体表面的发射率取决于物质种类、表面温度和表面状况，即仅与发射辐射的物体本身有关，而不涉及外界条件：

同一金属材料，高度磨光表面的发射率很小，而粗糙表面和受氧化作用后的表面发射率常常为磨光表面的数倍，在选用金属表面发射率时应注意表面状况；
大部分的非金属材料的发射率都很高，一般在0.85~0.95之间，且与表面状况包括颜色在内的关系不大，在缺乏资料时，可*似取作0.9.

例：试计算温度处于1400℃的碳化硅涂料表面的辐射力。
解：碳化硅涂料属于非导体，可*似认为 \(\varepsilon = \varepsilon_n\)，通过查表可知碳化硅涂料在1400℃时的 \(\varepsilon_n = 0.92\)，取 \(\varepsilon = 0.92\)，那么其辐射力为：

\[E = \varepsilon C_0 \left( \frac{T}{100} \right)^4 = 0.92 \times 5.67 \; W/(m^2 \cdot K^4) \times \left( \frac{1400+273.15}{100} \right) K^4 = 409000 \; W/m^2 = 409 \; kW/m^2 \]

一般工程手册中给出的发射率都是法向发射率，因此在使用的时候根据表面类型与状态进行相应的修正，对于本例，注意给定的温度范围是和发射率相对应的。

例：实验测得2500K的钨丝法向单色发射率如图所示，试计算其辐射力以及发光效率。

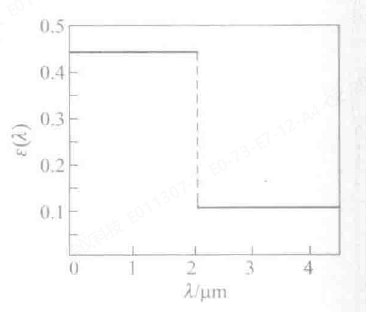
解：

（1）辐射力计算
根据图片可知，2500K温度下的钨丝，在\(0 \sim 2 \mu m\) 波段范围内的发射率为 0.45，在 \(2 \sim +\infty\) 波段范围内的发射率为0.1；
由公式可知，2500K的钨丝发射率为

\[\begin{aligned} \varepsilon &= \frac{E}{E_b} \\ &= \frac{\int_0^2 \varepsilon(\lambda) E_{b \lambda} d \lambda + \int_2^\infty \varepsilon(\lambda) E_{b \lambda} d \lambda}{E_b} \\ &= \frac{0.45 \int_0^2 E_{b \lambda} d \lambda + 0.1 \int_2^\infty E_{b \lambda} d \lambda}{E_b} \\ &= 0.45 \cdot \frac{\int_0^2 E_{b \lambda} d \lambda}{E_b} + 0.1 \cdot \frac{\int_2^\infty E_{b \lambda} d \lambda}{E_b} \\ &= 0.45 \cdot F_{b(0-2)} + 0.1 \cdot F_{b(2- \infty)} \\ & = 0.45 \cdot F_{b(0-2)} + 0.1 \cdot (1 - F_{b(0-2)}) \end{aligned} \]

根据 \(\lambda T = 2 \times 2500 = 5000 \mu m \cdot K\)，查询黑体辐射函数表可得：\(F_{b(0-2)} = 0.63372\)，代入上式有：

\[\varepsilon = 0.45 \times 0.63372 + 0.1 \times (1 - 0.63372) = 0.321802 \]

因此辐射力为：

\[\begin{aligned} E &= \varepsilon C_0 \left( \frac{T}{100} \right)^4 \\ &= 0.321802 \times 5.67 \times \left( \frac{2500}{100} \right)^4 \\ &= 712741.15 \; W/m^2 = 712.741 \; kW/m^2 \end{aligned} \]

（2）发光效率
由已知可得，发光效率：

\[\eta = \frac{可见光辐射力}{总辐射力} \]

可见光的波段为\(0.38 \sim 0.76 \mu m\)，该波段的光谱发射率就有

\[\begin{aligned} \varepsilon &= \frac{E}{E_b} \\ &= \frac{\int_{0.38}^{0.76} \varepsilon (\lambda) E_{b(\lambda)} d\lambda}{E_b} \\ &= \frac{0.45 \int_{0.38}^{0.76} E_{b(\lambda)} d \lambda}{E_b} \\ &= 0.45 F_{b(0.38-0.76)} \end{aligned} \]

有\(\lambda_1 T = 0.38 \times 2500 = 950 \mu m \cdot K\)，对应的光谱辐射占比\(F_{b(0-0.38)} = 0.0003\)，\(\lambda_2 T = 0.76 \times 2500 = 1900 \mu m \cdot K\)，对应的光谱辐射占比\(F_{b(0-0.76)} = 0.0521\)；
所以：\(F_{b(0.38-0.76)} = F_{b(0-0.76)} - F_{b(0-0.38)} = 0.0518\)，那么可见光波段的光谱发射率为

\[\varepsilon = 0.45 \times 0.0518 = 0.02331 \]

那么该波段的光谱辐射力为

\[\begin{aligned} E &= \varepsilon E_b \\ &= 0.02331 \times 5.67 \times \left( \frac{2500}{100} \right)^4 \\ &= 51628 \; W/m^2 = 51.628 \; kW/m^2 \end{aligned} \]

所以发光效率就有

\[\eta = \frac{51.628}{712.741} \approx 7.24 \% \]

可见白炽灯由于灯丝工作温度相对较低，热辐射中的可见光比例甚少，因此发光效率不高，大部分能量都位于红外波段。

3.2 气体的辐射特性

3.2.1 气体辐射的特点

3.2.2 光谱辐射能在气层中的定向传递

<暂不研究>

4. 实际物体对辐射能的吸收与辐射

4.1 实际物体的吸收比

对于黑体，发射率为1，吸收比也是1，此时发射比等于吸收比。对于实际物体，显然发射率小于1，即实际物体不能完全吸收投射到其表面上的辐射能，吸收比也小于1。定义单位时间内从外界投入到物体的单位表面积上的辐射能称为投入辐射（irradiation）。物体对投入辐射所吸收的百分比称为该物体的吸收比，吸收比是一个*均值，是投入到物体表面上各种不同波长辐射能的总体吸收比。实际物体的吸收比\(\alpha\)大小取决于两方面：

吸收物体本身状况：物质的种类、物体温度以及表面状况（粗糙度）；
投入辐射特性：光谱的吸收比以及光谱吸收的选择性。

物体吸收某一特定波长的辐射能的百分数称为光谱吸收比（Spectral Absorptivity），一般来讲，物体的光谱吸收比与波长有关。物体的光谱吸收比随波长而异的这种特性称为物体的吸收具有选择性。这一特性的应用场景有“温室效应”、焊接时佩戴的黑色眼镜等等。

“温室效应”：农业中培育蔬菜和花卉时，使用的暖房就利用了玻璃对辐射能吸收的选择性，太阳光照射到玻璃表面时，由于玻璃对于小于\(3 \mu m\)的辐射能的穿透比很大，而且太阳能的辐射能绝大部分位于可见光波段，从而使大部分太阳能进入暖房；由于暖房内温度相对较低，其辐射能绝大部分分布在大于\(3 \mu m\)以外的红外波段，而玻璃对于大于\(3 \mu m\)以外的波长吸收比很小，从而阻止了热量向外部散失。如图所示为某普通玻璃对于不同波长的电磁波的穿透比示意图。

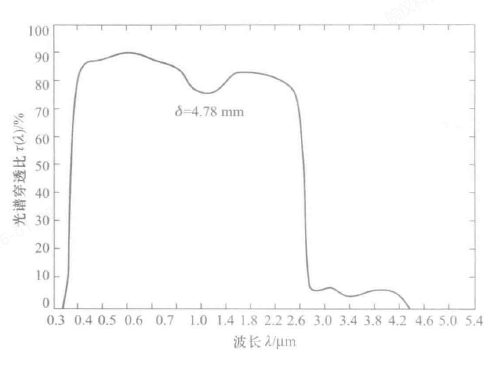
物体的颜色：

当阳光照射到一个物体表面上时，如果该物体能够吸收几乎所有的各种可见光，它就呈黑色；
如果该物体几乎全部反射可见光，它就呈白色；
如果该物体几乎均匀地吸收各色可见光并均匀地反射各色可见光，它就呈灰色；
如果该物体只反射了一种波长的可见光而几乎吸收其他所有的可见光，它就呈被反射的这种辐射线的颜色。

正是因为实际物体对不同波长的光谱吸收比具有选择性，在实际的工程问题中，吸收比的计算比较困难。物体的吸收比除与自身表面的性质和温度有关，还与投入辐射的表面性质和温度有关，因此物体的吸收比需要根据吸收一方和投入辐射一方两者的表面性质和温度有关。

如果投入辐射来自实际物体，物体1的吸收比可定义为

\[\begin{aligned} \alpha_1 &= \frac{\int_0^\infty \alpha (\lambda,T_1) \varepsilon (\lambda,T_2) E_{b \lambda} (T_2) d \lambda}{\int_2^\infty \varepsilon (\lambda,T_2) E_{b \lambda} (T_2) d \lambda} \\ &= f(T_1,T_2,表面1的性质,表面2的性质) \end{aligned} \]

如果投入辐射来自黑体，物体1的吸收比可定义为

\[\begin{aligned} \alpha &= \frac{\int_0^\infty \alpha (\lambda,T_1) E_{b \lambda} (T_2) d \lambda}{\int_2^\infty E_{b \lambda} (T_2) d \lambda} \\ &= \frac{\int_0^\infty \alpha (\lambda,T_1) E_{b \lambda} (T_2) d \lambda}{\sigma T_2^4} \\ &= f(T_1,T_2,表面1的性质) \end{aligned} \]

4.2 灰体的概念与工程应用

从上面可知，物体的光谱吸收比因波长长短而异，就会造成工程计算的复杂性。因此引入理想物体——灰体（Gray body）的概念，即物体的光谱吸收比与波长无关，\(\alpha (\lambda) = constant\)，不管投入辐射的分布如何，吸收比\(\alpha\)始终等于常数，亦即吸收比不受投入辐射物体影响，仅与自身表面性质以及表面温度有关。

灰体假设的前提是：只要所研究的波长范围内光谱吸收比基本上与波长分布无关，假设就成立，而不必要求在全波段范围内\(\alpha (\lambda)\) 为常数。在工程中常见的温度范围（\(T \leq 2000K\)），许多工程材料都具有这一特点，因此在工程手册中仅列出发射率的值，而不给出吸收比，原因也在此。对于漫射表面，光谱的吸收率和光谱发射率是相等的，对于漫射的灰体，称为漫灰体，在一定温度下，光谱发射比\(\varepsilon (\lambda)\)也与波长无关，也是个常数。

4.3 吸收比与发射率之间的关系——基尔霍夫定律（Kirchhoff's law）

在热*衡条件下，任何物体的自身辐射和它对来自黑体辐射的吸收比的比值，恒等于同温度下的黑体辐射力。简述为：热*衡时，任意物体对黑体投入辐射的吸收比等于同温度下该物体的发射率。即物体与黑体投入辐射处于热*衡时，物体的吸收比等于发射率。

如图所示，假定如图所示的两个相距很*的*板，从一块板上的辐射能全部落在另一块板上。

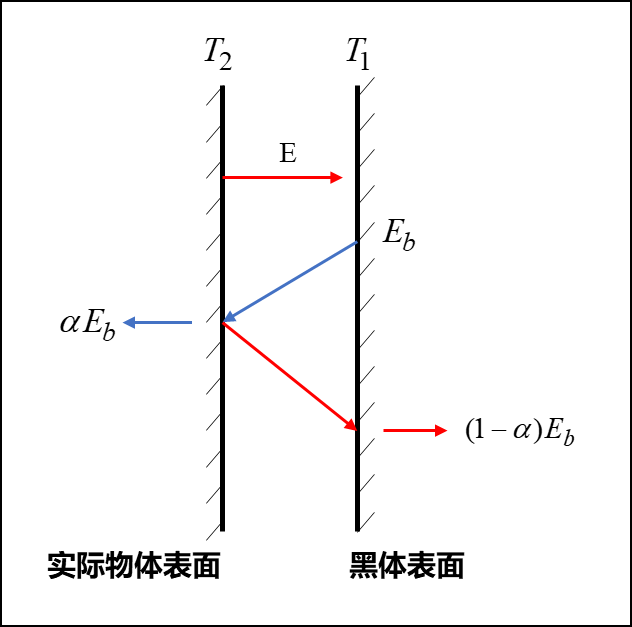
若板1为黑体表面，其辐射力、吸收比、表面温度分别为：\(E_b\)，\(\alpha_b = 1\)，\(T_1\)；板2为任意物体的表面，其辐射力、吸收比、表面温度分别为\(E\)，\(\alpha\)，\(T_2\)。现考察板2的能量收支差额，板2作为辐射源，单位面积上在单位时间内发射出的能量为\(E\)，两个面的能量吸收结果可如上图所示。板2支出与收入的差额即为两板间辐射传热的热流密度：

\[q = 向外辐射能量 - 吸收辐射能量 = E -\alpha E_b \]

当系统处于*衡时，即\(T_1 = T_2\)，热流密度\(q = 0\)，此时就有：\(E -\alpha E_b = 0\)，即\(E = \alpha E_b \Rightarrow \alpha = \frac{E}{E_b} = \varepsilon\)

基尔霍夫，德国物理学家，提出该理论仅25岁，他还在相变热力学和电路理论中做出了贡献。

对于漫灰体，不论投入辐射是否来自黑体，也不论是否处于热*衡状态下，其吸收比恒等于同温度下的发射率，因此如无特别说明均假定辐射表面是具有漫射特性（包括自身辐射和反射辐射）的灰体。

因此对于大多数情况下的物体，物体辐射力越大，其吸收能力越大，善于辐射的物体必善于吸收，反之亦然，因此同温度下黑体的辐射力最大。

4.4 太阳与环境辐射

太阳是一个巨大的热辐射体，直径为\(1.393 \times 10^9 \; m\)，是地球的109倍，太阳与地球之间的*均距离为\(1.5 \times 10^{11} \; m\)。

4.4.1 太阳常数

太阳*似于温度为\(5762 K\)的黑体辐射，其中 99% 的能量集中在\(0.2 \sim 3 \mu m\)的短波区域，最大能量位于\(0.48 \mu m\)的波长处。

在日地*均距离处，经测定，大气层外缘与太阳射线相垂直的单位表面积所接受到的太阳辐射能为\(1370±6 \; W/m^2\)，即太阳常数（Solar Constant），记为\(S_c\)，与地理位置或一天中的时间无关。

太阳辐射在穿过大气层时受到大气层两种削弱方式：

第一种是被包含在大气层中具有吸收能力的气体吸收，比如臭氧、水蒸气、二氧化碳、各种CFC气体等。臭氧和氧气主要吸收可见光波段，水蒸气和二氧化碳主要吸收红外波段；
第二种是散射作用（Scattering），即对太阳投入辐射的重新辐射（Irradiation），散射又分为分子散射（Rayleigh scattering）和米散射（Mie scattering）。分子散射表示向整个宇宙空间均匀进行，可认为一半射向宇宙空间，一半到达地面；米散射主要针对大气层中的尘埃和悬浮微粒，使得辐射能继续沿着投射方向射向地面，因此这一部分可认为完全到达地球表面上。

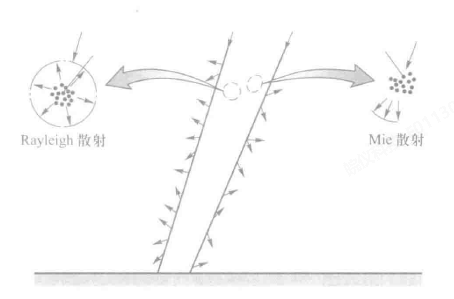
太阳辐射中没有经过吸收和散射的辐射能则直接到达地球表面，称为太阳的直接辐射。

5. 辐射计算以及辐射模型

6. Fluent 热辐射求解

7. Icepak 热辐射求解

8. FloEFD 热辐射求解

软件中可以定义并考虑来自计算域远场边界或者模型开口处的热辐射，即通过指定边界发射率和温度，或者/以及通过指定地理位置（地球表面）和时间（日期）或者通过一个常数或者随时间变化的方向（太阳照射角度）和强度来定义太阳辐射。另外假设工程流体既不发射也不吸收辐射能，对于热辐射是透明的。软件中有三种辐射模型，各自有各自的优点和使用限制：

离散传递模型（Discrete Transfer）：热辐射在一个确定的立体角范围内从表面单元离开的描述可以通过射线*似。辐射换热只通过辐射表面发出的一系列射线传递。当这些射线穿过流体和透明固体时，这些射线就会被追踪，直到射线碰到另一个辐射表面。该方法通常被称为射线追踪法（Ray Tracing），它能计算出交换系数——该系数是一个离散化的角系数，表示从一个辐射面发射出的总辐射能中被另一个辐射面所拦截的辐射能占比。在求解的初始阶段，会计算出辐射表面网格单元之间的交换系数，据此可以形成一个线性方程系统的系数矩阵。

该方法不适用于模拟吸收和波谱相关性仿真，适用于高温梯度或者辐射源集中的产品。

离散坐标模型（Discrete Ordinates）：该模型通过有限数量的离散立体角来求解辐射换热方程，每个立体角都对应一个矢量方向。该方法不仅能求解吸收性介质的辐射传热问题还能模拟光谱的依赖性。求解的精度取决于离散方向使用的数量。

该方法可用于波谱相关性的热辐射仿真，与离散传递不同，其主要用于热源分散的辐射，电子产品大多应用此模型，但不勾选波谱特性。该模型在三种模型中求解精度相对较低。在模型设置中环境辐射有三种：黑体光谱——只吸收辐射热，即热辐射波段；日光光谱——可见光光谱；外星太阳光——整个太阳光谱。

蒙特卡洛方法（Monte Carlo）：蒙特卡洛射线追踪法是一种统计方法，其核心思想是：特定环境中特定辐射表面的宏观行为分析模型，可以从微观层面上对辐射表面（或者吸收性介质）的行为的统计模型推导而来。为了实现这一点，该方法持续追踪从辐射表面或者吸收介质发射的光子的轨迹。该方法同样可以模拟介质中的吸收现象以及光谱依赖性，求解的精度取决于发射光子的数量。

该方法常用于LED产品的仿真

8.1 离散传递模型

8.1.1 基本假设

离散传递模型是基于通量模型的方法。具有以下假设前提：

固体表面的热辐射（包括自身发射和反射部分），除对称辐射面类型外，均假定为漫射辐射，即遵循兰贝特定律。根据该定律，单位投入辐射源面积、单位立体角内的辐射强度在所有方向上均相同。
未明确指定为黑体或白体的辐射固体表面，均假定为理想灰体。这意味着其具有与黑体相似的连续发射功率谱，因此其单色发射率不随发射波长变化。然而，对于特定材料和特定表面条件，灰体发射率可能依赖于表面温度。
表面对太阳辐射的吸收与反射，独立于来自所有其他热辐射源的热辐射（过程）。
传播中的热辐射在穿过被指定为“辐射透明”的固体时，不发生任何吸收。一个固体可被指定为：仅对太阳辐射透明；或对除太阳辐射外的所有热辐射源透明；或对热辐射与太阳辐射二者皆透明

8.1.2 离散传递方程

一般情况下，参与热辐射的表面可以发射、吸收和反射热辐射（包括太阳辐射和热引起的辐射）。离开辐射表面或者辐射源的热辐射可以通过公式描述为

\[Q^{out} _ T = \varepsilon \sigma T^4 A + (1 - \varepsilon)Q^{in}_T \]

式中：\(\varepsilon\) 表示表面发射率，\(\sigma\) 表示Stefan-Boltzmann 常量，\(T\) 表示表面温度，\(A\) 是辐射面面积，\(Q^{in} _ T\) 表示到达该表面的投入辐射。

8.2 离散坐标模型

8.2.1 基本假设

基于以下假设：

在计算域内的任意位置，整个4π立体角方向域被离散为指定数量的相等立体角。
吸收性（半透明）固体根据其指定的材料吸收系数来吸收和发射热辐射。此模型中不考虑散射效应。
不透明固体的表面根据其指定的发射率系数吸收入射热辐射，其余入射辐射则根据指定的镜面反射系数，以镜面反射、漫反射或二者结合的方式进行反射。
吸收性固体会发生镜面反射，且反射辐射会根据固体与相邻介质（可能是另一个吸收性固体，或是折射率恒定为1的透明固体或流体）的指定折射率发生折射。折射率数值不得超过4。

8.3 蒙特卡洛方法

8.3.1 基本假设