y-plus

1. \(y^+\) 简介

不论是高雷诺数流动还是低雷诺数流动，只要壁面为无滑移边界，近壁面附近必定存在较大的法向速度梯度。在距离壁面极小的法向距离内，速度从相对较大的值降至与壁面速度相同，甚至为0。因此对于近壁面法区域的求解，通常采用两种处理方式：一种是壁面函数法，二是加密网格，利用壁面模型法。至于这两种方法如何取，由 \(y^+\) 来体现。

壁面的存在对湍流流动影响显著，由于无滑移壁面的边界定义显然存在速度梯度。在离壁面非常近的区域内，粘性阻尼会削弱切向速度脉动，而运动阻塞则会减弱法向脉动；但在近壁区域的外侧部分，由于平均速度的大梯度导致湍流动能生成，湍流会迅速增强。

近壁建模对数值解的保真度影响重大，因为壁面是平均涡量和湍流的主要来源。毕竟，正是在近壁区域，求解变量的梯度较大，且动量及其他标量输运最为剧烈。因此，准确表征近壁区域的流动是成功预测壁面湍流的关键。

大量实验表明，近壁区域大致可分为三层。最内层称为粘性底层，其中流动几乎呈层流状态，分子粘性在动量及热量/质量输运中起主导作用。最外层称为完全湍流层，湍流在此起主要作用。最后，在粘性底层与完全湍流层之间还存在一个过渡区域，此处分子粘性与湍流的影响同等重要。如图为近壁面位置无量纲速度分布情况

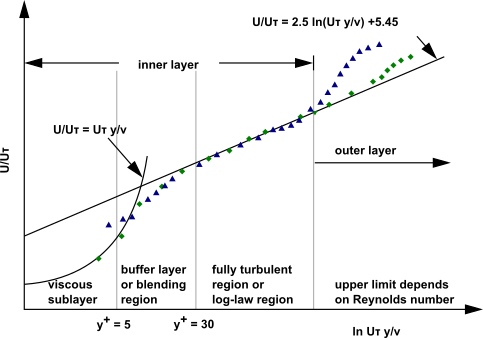
图中 \(y^+=\frac{y\rho u_{\tau}}{\mu}\)；纵坐标为无量纲速度 \(\frac{u}{u_{\tau}}\)。其中，\(u_{\tau}=\sqrt{\frac{\tau_w}{\rho}}\)，\(\tau_w\) 为壁面剪切应力，\(y\) 为壁面法向距离。从图 \(y^+<5\) 的区域，速度呈非线性形式，该区域通常称为粘性子层（viscous sublayer region）；在 \(y^+>60\) 的区域，速度与距离几乎呈线性趋势，该部分区域为完全发展湍流，也称为对数律区域（log law region）；两部分之间的区域，常称之为过渡子层（buffer layer region）。

估算 \(y^+\) 的一般步骤：

• 估算雷诺数：\(Re = \frac{\rho u L}{\mu}\) ；
• 估算壁面摩擦系数： \(C_f = 0.058Re^{-0.2}\)；
• 计算壁面剪切应力：\(\tau_w = \frac{1}{2}C_f\rho U_\infty^2\)，其中\(U_\infty\)为来流速度；
• 利用壁面剪切应力估算速度： \(u_\tau\)：\(u_\tau = \sqrt{\frac{\tau_w}{\rho}}\)；
• 计算第一层网格高度： \(y\)：\(y = \frac{y^+ \mu}{u_\tau \rho}\) 。

上面计算得到的 \(y^+\) 为估计值，通常需要根据计算结果来修正该值直至满足模拟要求。下面以平板流动来说明该计算过程：

• 雷诺数（\(Re\)）计算：公式\(Re = \frac{\rho u L}{\mu}\)，代入\(\rho = 1.225\)、\(u = 20\)、\(L = 1\)、\(\mu = 1.8×10^{-5}\) ，算出\(Re = 1.36×10^6\) ；
• 壁面摩擦系数（\(C_f\)）计算：公式\(C_f = 0.058Re^{-0.2}\)，代入雷诺数结果，算出\(C_f = 0.00344\) ；
• 壁面剪切应力（\(\tau_w\)）计算：公式\(\tau_w = \frac{1}{2}C_f\rho U_\infty^2\)，代入\(C_f\)、\(\rho\)、\(U_\infty = 20\) ，算出\(\tau_w = 0.843\mathrm{kg/(m\cdot s^2)}\)；
• 速度（\(u_\tau\)）计算：公式\(u_\tau = \sqrt{\frac{\tau_w}{\rho}}\)，代入\(\tau_w\)、\(\rho\) ，算出\(u_\tau = 0.83\mathrm{m/s}\)；
• 第一层网格高度（\(y\)）计算：公式\(y = \frac{y^+ \mu}{u_\tau \rho}\)，代入\(y^+ = 50\)、\(\mu\)、\(u_\tau\)、\(\rho\) ，算出\(y = 8.851×10^{-4}\mathrm{m}\) ，即第一层网格高度约为\(8.851×10^{-4}\mathrm{m}\) 。

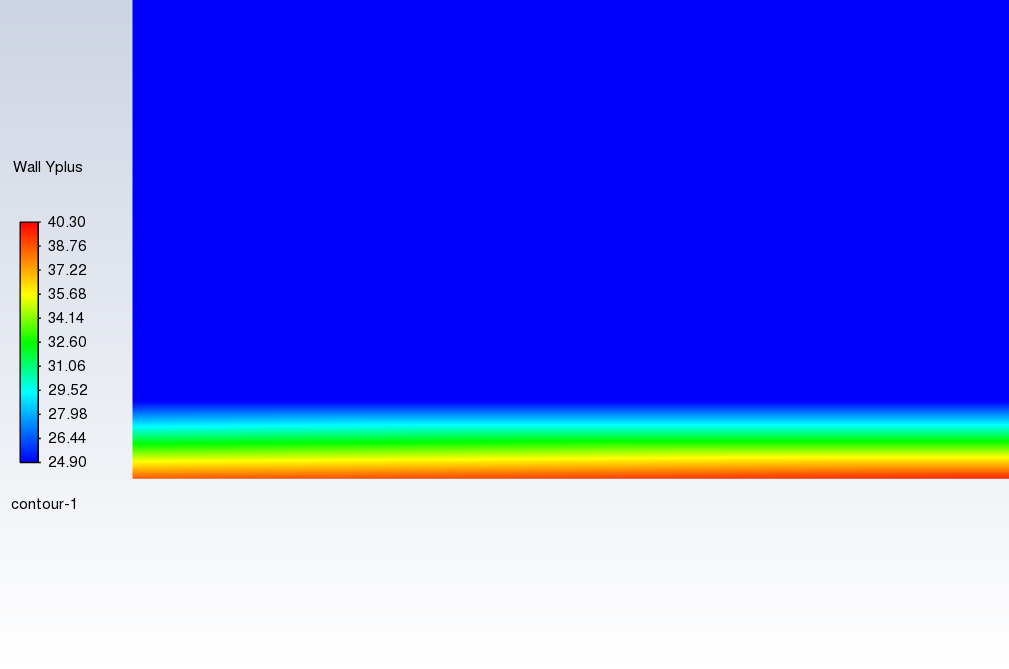
以下为仿真结果：采用两方程 \(k-\omega \; sst\) 湍流模型，其中 \(k-\epsilon\) 湍流模型计算的偏低 \(30~40\)，采用增强型壁面函数与该结果类似，并且 \(S-A\) 模型也与之类似。

2. 壁面函数 vs. 近壁模型

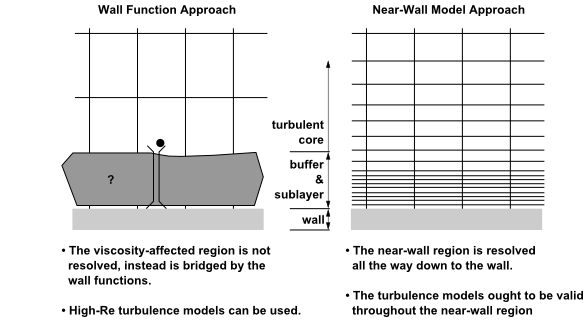
传统上，近壁区建模有两种方法。其中一种方法不解析受粘性影响的内区（inner region）（粘性底层和过渡层），而是使用称为壁面函数的半经验公式，来充当位于壁面与完全湍流区之间（受粘性影响区域）数据传递的桥梁。壁面函数的使用避免了对湍流模型进行修正以考虑壁面存在的需要。

另一种方法通过对湍流模型进行修正，使得受粘性影响区域能够通过网格直接解析至壁面（包括粘性底层）。为便于讨论，这将被称为“近壁建模”方法。这两种方法在下图中以示意图形式展示。

所有壁面函数（可扩展壁面函数除外）的主要缺点是，在壁面法向网格细化时，数值结果会变差。\(y^+\) 值小于15时，壁面剪切应力和壁面传热将逐渐产生无界误差。尽管这曾是若干年前的工业标准，但 Ansys Fluent 已采取措施提供更先进的壁面函数，这些公式允许进行一致的网格细化而不导致结果变差。此类 \(y^+\) 无关公式是所有基于 \(ω\) 方程的湍流模型的默认设置。对于基于 \(ε\) 方程的模型，Menter-Lechner方法和增强壁面处理（EWT）起到相同作用。 \(y^+\) 不敏感壁面处理同样是Spalart-Allmaras模型的默认设置，允许您在无需考虑近壁 \(y^+\) 分辨率的情况下运行该模型。

仅当边界层的整体分辨率足够时，才能获得高质量的壁面边界层数值结果。这一要求实际上比达到特定的 \(y^+\) 值更为重要。准确覆盖边界层的最小单元数约为10，但20是理想的。对于非结构化网格，为准确预测壁面边界层建议在近壁区域生成10-20层或者更多的棱柱层单元。棱柱层的厚度应确保约 15 个或更多节点实际覆盖边界层。这可以在求解后通过观察湍流粘度来检查，湍流粘度在边界层中间有一个最大值--这个最大值给出了边界层的厚度（最大值的两倍位置给出了边界层边缘）。棱柱层必须比边界层厚，否则棱柱层有可能限制（仿真过程中）边界层的增长（影响边界层捕捉精度）。

使用近壁建模方法时，如果求解粘性子层，需要保证 \(y^+ ≈1\) ，对于湍流模型需要选择低雷诺数湍流模型，适用于壁面对计算结果非常重要的情况，如气动阻力计算、旋转机械叶片性能等。但是此时壁面函数不可用，壁面函数适用于第一层网格尺寸 \(30<y^+<300\) 的情况，此时通常使用高雷诺数湍流模型，如 \(标准k-\epsilon\) 模型、\(Realizable \; k-\epsilon\) 模型、\(RNG \; k-\epsilon\) 模型。一般来说对于粘性子层区域的捕捉精度不高时使用。

3. Fluent中的壁面函数模型

这是关于计算流体动力学（CFD）中壁面处理方法的技术内容，具体信息如下：
（1） 不同流动场景下壁面函数/处理方法的选用规则：
- 高雷诺数（\(Re>10^6\) ）且有流动分离、再附或射流情况，用标准或非平衡壁面函数，非平衡壁面函数适配复杂流动形态。
- 低雷诺数或需精确求解壁面附近贴体流动特征（如边界层精细结构 ），采用增强壁面处理方法。
（2） 增强壁面处理的模型适配性：是SA模型（Spalart - Allmaras模型 ）、k - omega模型的默认壁面处理，也可用于k - epsilon模型、雷诺应力模型（RSM），用于指导CFD模拟中壁面流动数值计算的设置，优化模拟精度 。