流体以及数学描述

1. 流体以及数学描述

在开始得出描述流体行为的基本方程之前，为了方便起见，不妨先解释一下流体动力学（fluid dynamics）一词的含义。实际上，流体动力学就是研究大量单独粒子之间的相互作用的运动，在研究的范畴内它们是原子或者分子。这就意味着，假设流体的密度足够大，以至于可以将它们近似成连续体。这表示即使一个无穷小的流体单元仍然包含足够多的粒子，这样我们可以为它们指定平均速度和平均动能。通过这种方法，流体中的每一个点都可以定义速度、压力、温度、密度以及其他重要的物理量。

流体力学主要方程的推导是基于这样一个事实：流体的动力学行为有下面的守恒定律决定，即

• 质量守恒
• 动量守恒
• 能量守恒

某个流动物理量的守恒意味着：它在任意控制体内的总变化可以表示为该物理量穿过边界的输运量、任何内力和内部源项以及作用在该控制体上的外力的净效应。穿过边界的量称为通量。

通量一般可分解为两个不同的部分：第一部分是由于对流传输，第二部分是由于静止流体中的分子热运动。第二部分是扩散性质的--它与所考虑的物理量的梯度成正比，因此在均匀分布（不存在物理梯度）的情况下会消失。

通过对守恒定律的讨论，我们很自然地想到了将流场划分为若干体积，并集中研究流体在这样一个有限区域内的行为模型。为此，我们定义了所谓的有限控制体，并尝试对其物理特性进行数学描述。

1.1. 有限控制体

考虑图中以流线形式表示的一般流场，由闭合曲面 \(\partial \Omega\) 围成且固定在空间中的任意有限区域的流动，定义该区域为控制体 \(\Omega\)。

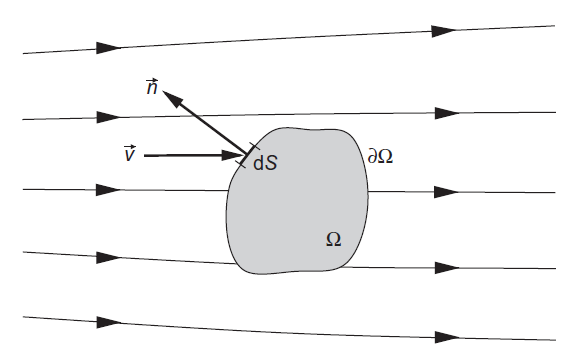
同时也可以引入面积微元 \(dS\) 以及与之相联系的指向外部的单位法向量 \(\vec n\) 。单位体积的标量 \(U\) 的守恒定律表明，其在区域 \(\Omega\) 内随时间的变化为

\[\frac{\partial}{\partial t}\int_{\Omega}U\mathrm{d}\Omega \]

上式就等于对流通量的贡献总和——大量的 \(U\) 以 \(\vec v\) 的速度穿过边界进入控制体内

\[-\int_{\partial\Omega}U(\vec{v}\cdot\vec{n})dS \]

进一步由于扩散通量——用广义菲克梯度定律表示

\[\int_{\partial\Omega}\kappa\rho[\nabla(U / \rho)\cdot\vec{n}]dS \]

其中 \(\kappa\) 表示热扩散系数，最后由于体积源项 \(Q_V\) 以及面源相 \(Q_S\) 即：

\[\int_{\Omega} Q_V d\Omega+\oint_{\partial\Omega}(\vec{Q}_S\cdot\vec{n})dS \]

将上述的贡献汇总之后，可以得到下面关于守恒标量 \(U\) 的守恒形式：

\[\frac{\partial}{\partial t}\int_{\Omega}U\mathrm{d}\Omega+\oint_{\partial\Omega}\left[U(\vec{v}\cdot\vec{n})-\kappa\rho(\nabla U^{*}\cdot\vec{n})\right]\mathrm{d}S = \int_{\Omega}Q_{V}\mathrm{d}\Omega+\oint_{\partial\Omega}(\vec{Q}_{S}\cdot\vec{n})\mathrm{d}S \tag{1} \]

其中 \(U^*\) 表示单位质量的标量 \(U\) ，即 \(U/\rho\) 。

需要重点注意的是，守恒变量如果是向量而不是标量时，方程1的形式仍然可用。但是不同的是，对流和扩散通量为张量而不是向量——\(\overline{\overline{F}}_C\) 为对流通量张量，\(\overline{\overline{F}}_D\) 为扩散通量张量。体积源项为向量 \(\vec{Q}_V\)，面元源项变成张量 \(\overline{\overline{Q}}_C\)，根据守恒定律针对向量 \(\vec{U}\) 有：

\[\frac{\partial}{\partial t}\int_{\Omega} \vec{U} \mathrm{d}\Omega + \oint_{\partial\Omega} \left[(\overline{\overline{F}}_C - \overline{\overline{F}}_D) \cdot \vec{n} \right] \mathrm{d}S = \int_{\Omega} \vec{Q}_v \mathrm{d}\Omega + \int_{\partial\Omega} (\overline{\overline{Q}}_S \cdot \vec{n}) \mathrm{d}S \tag{2} \]

上面两个方程就是守恒定律的积分形式，它拥有两个非常重要且可取的性质：

• 如果不存在体积源项，变量U只由穿过控制体边界 \(\partial \Omega\) 的通量决定，不受任何控制体内的通量影响。
• 对于非连续流场，比如激波间断区域或者接触间断区域，守恒形式仍然是适用的。

由于其通用性和可取性，当今大多数CFD程序基于控制方程的积分形式也就不足为奇了。在接下来的章节中，我们将利用上述积分形式，推导出流体力学的三个守恒定律的相应表达式。

注意：Diffusive——指扩散，而非耗散，扩散即存在物理梯度时发生，而耗散则是指能量的不可逆损失，比如超音速运动的飞行器，气动热的产生就是由于强烈的粘性耗散，动能转换成热能，且这种转换不可逆。

2. 守恒定律

2.2.1. 连续性方程

如果我们专注于单相流动，质量守恒定律表述的事实是：质量不会在流场中凭空产生，也不会凭空消失。连续性方程中也没有扩散通量的贡献，因为对于静止的流体，任何质量的变化都会导致流体粒子的位移。

连续性方程中流体的质量守恒是通过宏观运动（对流）体现，而非分子的扩散（微观分子作用）。在一般的守恒方程中，比如动量方程、能量方程中，扩散通量通常表示由分子运动引起的输运（粘性应力，热传导）。

为了推导出连续性方程，考虑固定在空间中的有限控制体模型，控制面上一点，流速为 \(\vec{v}\) ，单位法向量为 \(\vec{n}\) ，\(dS\) 表示面积微元。连续性方程中的守恒量是密度 \(\rho\) ，在有限控制体内总质量随时间的变化率就有：

\[\frac{\partial}{\partial t}\int_{\Omega}\rho\mathrm{d}\Omega \]

质量流量就可以表示成：密度×面积×垂直于表面的速度分量，因此穿过每个面元 \(dS\) 的对流通量贡献为：

\[\rho(\vec{v} \cdot \vec{n})dS \]

因为对流法向量 \(\vec{n}\) 总是指向控制体外部，如果 \((\vec{v} \cdot \vec{n})\) 为负，则表示流入控制体，如果为正，则表示流出控制体，因此质量流出控制体。正如上所述，不存在体积源项和面源项，因此，考虑方程1的一般形式：

\[ \frac{\partial}{\partial t} \int_{\Omega} \rho \, \mathrm{d}\Omega + \oint_{\partial\Omega} \rho (\vec{v} \cdot \vec{n}) \, \mathrm{d}S = 0 \tag{3} \]

这就是连续性方程的积分形式——质量守恒定律。

2.2.2. 动量方程

牛顿第二定律指出，动量的变化是由作用在质量单元上的净力引起的。对于控制体 \(\Omega\) 上无穷小的部分有：

\[\rho \vec{v} d \Omega \]

控制体内动量随时间的变化为

\[\frac{\partial}{\partial t} \int_{\Omega} \rho \vec{v} d \Omega \]

因此，守恒变量可以写成速度与密度的乘积形式

\[\rho \vec{v}=[\rho u,\rho v,\rho w]^T \]

描述穿过控制体边界的动量输运的对流通量张量是由笛卡尔坐标系中各个分量组成

\[\begin{aligned} \begin{cases} x&-分量 \rho u \vec{v} \\ y&-分量 \rho v \vec{v} \\ z&-分量 \rho w \vec{v} \end{cases} \end{aligned} \]

动量守恒中，对流通量张量的贡献为

\[- \oint_{\partial \Omega} \rho \vec{v}(\vec{v} \cdot \vec{n}) dS \]

对于静止的流体没有动量的扩散，所以扩散通量为0。因此现在剩下的问题就是，流体单元受到什么力作用？我们可以确定作用在控制体上的两种力，即

• 外部体积力，直接作用在控制体质量上的力。比如重力、浮力、科氏力或者向心力。在特定的案例中，也可以有电磁力的存在。
• 面力，直接作用在控制体表面上的力，由下面两种源项产生：
  （a）由控制体周围流体施加的压力分布；
  （b）流体与控制体表面之间摩擦产生的剪应力和正应力。
  综上，每单位体积的体力用 \(\rho \vec{f_e}\) 表示，对应方程2中的体积源项。因此，外部体力对动量守恒方程的贡献为

\[\int_{\Omega} \rho \vec{f_e} d\Omega \]

面源项包含两部分——均匀分布的压力和粘性应力张量，即

\[\overline{\overline{Q}}_S=-p \overline{\overline{I}} + \overline{\overline{\tau}} \tag{4} \]

如下图为，作用在控制体面元上的面力

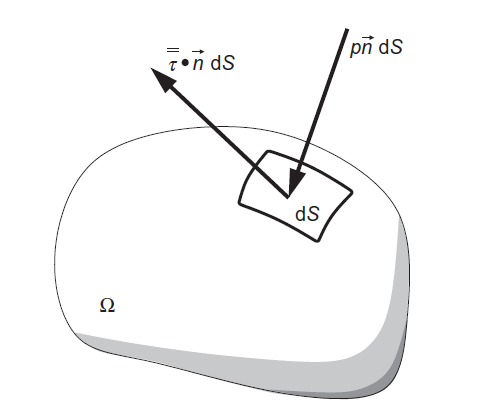
\(\overline{\overline{I}}\) 表示单位张量，控制体上的面源项的影响如上图所示，我们将更详细的阐述应力张量的形式，特别说明正应力和剪应力是如何与流速联系的。

因此，总结上面各种情况对一般守恒形式（方程2）的贡献可以得出固定在空间中的任意控制体 \(\Omega\) 内动量守恒方程的表示

\[ \frac{\partial}{\partial t} \int_{\Omega} \rho \vec{v} \, \mathrm{d}\Omega + \oint_{\partial\Omega} \rho \vec{v} (\vec{v} \cdot \vec{n}) \, \mathrm{d}S = \int_{\Omega} \rho \vec{f} \, \mathrm{d}\Omega - \oint_{\partial\Omega} p \vec{n} \, \mathrm{d}S + \oint_{\partial\Omega} (\overline{\overline{\tau}} \cdot \vec{n}) \, \mathrm{d}S \tag{5} \]

2.2.3. 能量方程

我们在推导能量方程时要用到的基本原理是热力学第一定律。应用在开始章节中的控制体中时，表示控制体内总能随时间发生的任何改变是由于作用在体积上的力的功率以及进入控制体内的净热通量引起的。流体单位质量的总能 \(E\) 等于单位质量的内能 \(e\) 和 单位质量的动能 \(|\vec{v}|^2/2\) 之和，因此总能为

\[E=e+\frac{|\vec{v}|^2}{2}=e+\frac{u^2+v^2+w^2}{2} \tag{6} \]

在能量守恒方程中守恒变量为单位体积的总能，即 \(\rho E\) ，在控制体内其随时间的变化可以表示为

\[\frac{\partial}{\partial t} \int_{\Omega} \rho E d \Omega \]

根据一般守恒定律推导中的讨论，我们可以指定对流通量的贡献为

\[- \oint_{\partial \Omega} \rho E(\vec{v} \cdot \vec{n}) dS \]

相较于连续性方程和动量方程，能量方程中包含扩散通量。正如我们已经讨论的，扩散通量与单位质量的守恒变量的梯度成正比（Fick's law）。因为扩散通量是为静止而流体定义的，只有内能才是有意义的，因此有

\[\vec{F}_D = - \gamma \rho \kappa \nabla e \tag{7} \]

式中， \(\gamma = c_p/c_v\) 为比热比，\(\kappa\) 表示热扩散系数。扩散通量表示一部分热通量进入控制体内的，即由于分子热传递引起的热扩散——由于温度梯度引起的热传递。因此方程7一般以傅里叶热传导定律的形式书写，即

\[\vec{F}_D = -k \nabla T \tag{8} \]

其中，\(k\) 导热系数，\(T\) 为绝对静温。
进入控制体内的另一部分静热通量，是由辐射的吸收和发射或者化学反应引起的体积热。使用 \(\dot q_h\) 表示热源——单位体积热传导随时间的变化率。结合体力\(\vec{f}_e\) 的功率，将这一项引入到动量方程中，完善体积源项

\[Q_V = \rho \vec{f_e} \cdot \vec{v} + \dot q_h \tag{9} \]

对能量守恒方程的最后一个贡献项—— \(Q_S\) 还没有确定，该源项对应于压力以及正应力和剪应力在流体单元上所做的功率，即

\[\vec{Q}_S = -p \vec{v} + \overline{\overline \tau} \cdot \vec{v} \tag{10} \]

对上述所有贡献和项进行排序后，我们得到能量守恒方程的如下表达式

\[\begin{equation} \begin{aligned} \frac{\partial}{\partial t} \int_{\Omega} \rho E \, \mathrm{d}\Omega + \oint_{\partial\Omega} \rho E (\vec{v} \cdot \vec{n}) \, \mathrm{d}S = \oint_{\partial\Omega} k (\nabla T \cdot \vec{n}) \, \mathrm{d}S + \int_{\Omega} \left( \rho \vec{f}_e \cdot \vec{v} + \dot{q}_h \right) \, \mathrm{d}\Omega \\ \quad - \oint_{\partial\Omega} p (\vec{v} \cdot \vec{n}) \, \mathrm{d}S + \oint_{\partial\Omega} (\overline{\overline{\tau}} \cdot \vec{v}) \cdot \vec{n} \, \mathrm{d}S. \tag{11} \end{aligned} \end{equation} \]

方程11通常写成与上式稍微不同的形式，为此，我们将根据总焓、总能和压力之间的关系来改写上式

\[H = h + \frac{|\vec{v}|^2}{2} = E + \frac{p}{\rho} \tag{12} \]

焓是指系统的总能量，上式中 \(h = e + \frac{p}{\rho}\) ，焓 = 热力学能 + 压力势能（单位质量的压力）。因此总焓 \(H = h + \frac{|\vec{v}|^2}{2} = e + \frac{p}{\rho} + \frac{|\vec{v}|^2}{2} = E + \frac{p}{\rho}\)

在应用能量守恒定律时，结合对流项—— \(\rho E \vec{v}\) 和压力项—— \(p \vec{v}\) ，能量方程的最终形式为

\[\frac{\partial}{\partial t}\int_{\Omega} \rho E \mathrm{d}\Omega + \oint_{\partial\Omega} \rho H(\vec{v} \cdot \vec{n}) \mathrm{d}S = \oint_{\partial\Omega} k(\nabla T \cdot \vec{n}) \mathrm{d}S + \int_{\Omega} (\rho \vec{f}_e \cdot \vec{v} + \dot{q}_h) \mathrm{d}\Omega + \oint_{\partial\Omega} (\overline{\overline{\tau}} \cdot \vec{v}) \cdot \vec{n} \mathrm{d}S \tag{13} \]

我们已经推导出三大守恒定律方程：质量守恒、动量守恒和能量守恒。下一节，我们将弄清楚方程中的正应力项和剪应力项。

3. 粘性应力

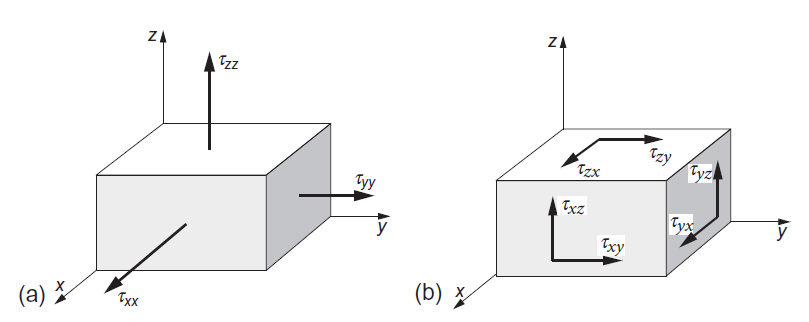
粘性应力源于流体与单元面之间的摩擦作用，用粘性应力张量 \(\overline{\overline{\tau}}\) 来描述。在笛卡尔坐标系中，它的通用形式为：

\[\overline{\overline{\tau}} = \begin{bmatrix} \tau_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yx} & \tau_{yy} & \tau_{yz} \\ \tau_{zx} & \tau_{zy} & \tau_{zz} \end{bmatrix} \quad \text{其中} \quad \begin{aligned} \begin{cases} \tau_{xy} &= \tau_{yx}, \\ \tau_{xz} &= \tau_{zx}, \\ \tau_{yz} &= \tau_{zy} \end{cases} \end{aligned} \tag{14} \]

符号 \(\tau_{ij}\) 表示作用在垂直于 \(i\) 轴的平面且沿 \(j\) 轴方向的应力。应力分量 \(\tau_{xx}\)、\(\tau_{yy}\)、\(\tau_{zz}\) 表示正应力，其他分量分别表示剪应力。如图所示为六面体流体单元的应力分布。从图中可以看出，互相垂直的正应力试图使单元表面发生位移，剪应力试图剪切单元。

现在你可能会问，粘性应力如何计算的呢？首先，其取决于介质的动力学属性，对于流体比如空气或者水，Newton 指出切应力正比于速度梯度。因此，这种介质称为牛顿流体。另一方面，比如融化的塑料或者血液就是另一种情况——都属于非牛顿流体。对于绝大多数的实际问题，流体都可以假设为牛顿流体，应力张量的分量为

\[\begin{aligned} \tau_{xx} &= \lambda \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} \right) + 2\mu \frac{\partial u}{\partial x} \\ \tau_{yy} &= \lambda \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} \right) + 2\mu \frac{\partial v}{\partial y} \\ \tau_{zz} &= \lambda \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} \right) + 2\mu \frac{\partial w}{\partial z} \\[6pt] \tau_{xy} &= \tau_{yx} = \mu \left( \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x} \right) \\ \tau_{xz} &= \tau_{zx} = \mu \left( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \right) \\ \tau_{yz} &= \tau_{zy} = \mu \left( \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y} \right) \end{aligned} \tag{15} \]

\(\lambda\) 表示第二粘度系数（second viscosity），\(\mu\) 表示动力粘度系数，出于便利，我们可以定义运动粘度系数 \(\nu\)：

\[\nu = \frac{\mu}{\rho} \tag{16} \]

方程15是由英国人斯托克斯（George Stokes）在19世纪推导出，其中 \(\mu(\partial u / \partial x)\)等在正应力的项表示线性变形——形状的改变，另一方面，\(\lambda div\vec{v}\) 表示体积膨胀——体积变化率，实质上是密度的变化。

以 \(\tau_{xx}\) 为例说明：
\(\tau_{xx} = \underbrace{\lambda \left( \epsilon_{xx} + \epsilon_{yy} + \epsilon_{zz} \right)}_{\text{体积膨胀项}} + \underbrace{2\mu \epsilon_{xx}}_{\text{线性变形项}}\)

• \(\lambda\) 项表示体积膨胀项：通过 \(\lambda\) 表示材料对变形的抵抗，其中 \(\epsilon_{xx} + \epsilon_{yy} + \epsilon_{zz} = \nabla \cdot \mathbf{u}\) 表示体积膨胀率。
• \(2\mu\) 项表示线性变形项：通过动力粘度系数反应材料在 \(x\) 方向上的纯线性变形—— \(\epsilon_{xx} = \partial u/\partial x\) 为 \(x\) 方向上的线应变。

为了封闭正应力方程组，斯托克斯引入经验公式：

\[\lambda = \frac{2}{3} \mu = 0 \tag{17} \]

上式被称为体积粘度。体积粘度表示在温度均匀分布的流体中，在体积以有限速率变化时的能量耗散特性。

除了极高的温度或者压力外，迄今为止还没有实验证据能够推翻这一假设。因此一般使用方程17结合方程15消除 \(\lambda\)，因此粘性正应力为

\[\begin{aligned} \tau_{xx} &= 2\mu \left( \frac{\partial u}{\partial x} - \frac{1}{3}\text{div}\vec{v} \right), \\ \tau_{yy} &= 2\mu \left( \frac{\partial v}{\partial y} - \frac{1}{3}\text{div}\vec{v} \right), \\ \tau_{zz} &= 2\mu \left( \frac{\partial w}{\partial z} - \frac{1}{3}\text{div}\vec{v} \right). \end{aligned} \tag{18} \]

值得注意的是，对于不可压缩流体（常密度），由于速度的散度为0（连续性方程），上式对正应力的表达式将得到简化。

有待确定的是作为流体状态函数的粘度系数 \(\mu\) 和导热系数 \(k\) 。这只能在连续介质力学的框架内根据经验假设来完成。我们将在下一节再讨论这个问题。

4. N-S方程

在上一节中，我们分别推导出了质量守恒定律、动量守恒定律以及能量守恒定律。为了更好地体现每一个物理项所具有的意义，现在可以将这些方程整合成一个方程系统。为此，我么回到向量的一般守恒定律，即方程2。出于以下原因，我们将会引入两个通量向量：\(\vec{F_C}\)，\(\vec{F_V}\)。第一个向量跟流体中对流输运量相关，通常被称为对流通量矢量，不过对于动量和能量方程该项还分别包括压力项 \(p\vec{n}\) （方程5）和 \(p(\vec{v} \cdot \vec{n})\) （方程11）。第二个通量向量——称为粘性通量向量 \(\vec{F_V}\)，包含粘性应力以及热扩散。除此之外，让我们来定义一个源项 \(\vec{Q}\)，其包括由体积力和体积热组成的体积源项。

考虑这些之后，与单位法向量 \(\vec{n}\)相乘得到向量积，结合方程2、3、5和13得到

\[\frac{\partial}{\partial t}\int_{\Omega} \vec{W}\, \mathrm{d}\Omega + \oint_{\partial\Omega} (\vec{F}_c - \vec{F}_v)\, \mathrm{d}S = \int_{\Omega} \vec{Q}\, \mathrm{d}\Omega \tag{19} \]

守恒变量的向量形式 \(\vec{W}\) 在三维中由下面5个分量组成

\[\vec{W}=\begin{bmatrix} \rho\\ \rho u\\ \rho v\\ \rho w\\ \rho E \end{bmatrix} \tag{20} \]

对于对流通量向量 \(\vec{F_C}\) 有

\[\vec{F}_c = \begin{bmatrix} \rho V\\ \rho u V + n_x p\\ \rho v V + n_y p\\ \rho w V + n_z p\\ \rho H V \end{bmatrix} \tag{21} \]

正交于面积微元的逆变速度被定义为：速度向量与各个方向上的单位法向量之间的标量积，即：

\[V \equiv \vec{v}\cdot\vec{n}=n_x u + n_y v + n_z w \tag{22} \]

方程21中的总焓 \(H\) 由方程12给出。结合方程14对于粘性通量向量就有

\[\vec{F}_v = \begin{bmatrix} 0 \\ n_x \tau_{xx}+n_y \tau_{xy}+n_z \tau_{xz}\\ n_x \tau_{yx}+n_y \tau_{yy}+n_z \tau_{yz}\\ n_x \tau_{zx}+n_y \tau_{zy}+n_z \tau_{zz}\\ n_x \Theta_x + n_y \Theta_y + n_z \Theta_z \end{bmatrix} \tag{23} \]

其中

\[\begin{align*} \Theta_x &= u\tau_{xx}+v\tau_{xy}+w\tau_{xz}+k\frac{\partial T}{\partial x}\\ \Theta_y &= u\tau_{yx}+v\tau_{yy}+w\tau_{yz}+k\frac{\partial T}{\partial y}\\ \Theta_z &= u\tau_{zx}+v\tau_{zy}+w\tau_{zz}+k\frac{\partial T}{\partial z} \end{align*} \tag{24} \]

上式分别描述了流体中粘性应力和热传递所做的功，最后，源项 \(\vec{Q}\) 可以写成

\[\vec{Q}=\begin{bmatrix} 0\\ \rho f_{e,x}\\ \rho f_{e,y}\\ \rho f_{e,z}\\ \rho \vec{f}_e\cdot\vec{v}+\dot{q}_h \end{bmatrix} \tag{25} \]

对于牛顿流体而言，如果粘性应力之间存在方程15中描述的关系，上面方程 19-25 组成的方程系统就是 \(Navier-Stokes \; equations\)。它们描述了穿过固定在空间中的控制体 \(\Omega\) 的边界 \(\partial \Omega\) 的质量、动量和能量的交换（通量形式）。根据守恒定律我们已经推导出了 N-S 方程的积分形式。应用高斯定理，方程19可以改写成微分形式。由于文献中经常出现微分形式，未完整起见，将其纳入其他章节进行详细描述。

在一些案例中，比如涡轮机械中的应用或者大气物理学，控制体关于某个轴是旋转的（通常是静止的）。在这种情况下， N-S 方程转换成旋转参考系下的描述。因此，由于科里奥利力（科氏力）以及向心力的作用源项 \(\vec{Q}\) 需要进一步扩展。

对于其他情形，控制体会出现平移或者变形，比如会出现在流固耦合的情形中。接着，N-S 方程必须扩展一个项，即用于描述面元 \(dS\) 相对于固定参考系的运动。另外，所谓的 \(geometric \; conservation \; law\) 也必须满足。在其他章节我们再具体描述。

N-S 方程是由5个守恒变量 \(\rho,\rho u,\rho v,\rho w,\rho E\) 组成的三维方程系统。但是方程组包含7个未知的流场变量，分别是：\(\rho,u,v,w,E,p,T\)。因此，我们必须额外增加两个方程，用于描述状态变量之间的热力学关系。比如，压力可以描述为密度和温度的函数，内能或者焓是温度和压力的函数。除此之外，我们必须提供粘性系数 \(\mu\) 和热传导系数 \(k\) 作为流体的状态函数以便完全封闭整个方程组。显然，这些关系取决于考虑的流体类型。下面，我们将展示两种常见情形中封闭方程组的方法。

4.1. 理想气体状态方程

在纯空气动力学中，通常将工作流体的行为合理的假设成热量完全气体，状态方程形式为

\[p = \rho R T \tag{26} \]

\(R\) 表示特定的气体常数。焓的表示形式为

\[h = c_p T \tag{27} \]

用保守变量来表示压力是很方便的。为此，我们必须将总焓与总能量的关系式 (方程12) 与状态方程 （方程26) 结合起来。将焓的表达式 (方程27) 代入并使用以下定义

\[R = \frac{c_p}{c_v}，\gamma = \frac{c_p}{c_v} \tag{28} \]

最后得到压力表达式、

\[p = (\gamma - 1)\rho\left[E - \frac{u^{2}+v^{2}+w^{2}}{2}\right] \tag{29} \]

然后借助以下关系式计算温度，对于理想气体动力粘度系数 \(mu\) 与温度强相关但是与压力弱相关。萨瑟兰（Sutherland）方程经常被使用，对于空气该方程的形式为

\[\mu = \frac{1.45T^{3/2}}{T + 110}\cdot 10^{-6} \tag{30} \]

温度T单位为开尔文，在 \(T = 288K\) 时，得到 \(\mu = 1.78 \times 10^{-5}kg/m \cdot s\)，导热系数 \(k\) 的温度依赖性与气体中的 \(\mu\) 相似。相比之下，液体的 \(k\) 几乎是恒定的。因此

\[k = c_p \frac{\mu}{\Pr} \tag{31} \]

该方程通常用于空气，另外，通常假设整个流体域中的普朗特数 \(Pr\) 是常数，对于空气普朗特数取值为 \(Pr = 0.72\)。

4.2. 真实气体状态方程

当我们必须处理真实气体时，问题就变得更加复杂了。原因在于，除了流体动力学之外，我们现在还必须模拟热力学过程和化学反应。真实气体流动的例子包括燃烧模拟、重返大气层飞行器的高超音速流动或蒸汽轮机中的流动。

原则上，可以采用两种不同的方法来解决问题。第一种方法适用于气体处于化学平衡和热力学平衡状态的情况。这意味着存在唯一的状态方程。因此，控制方程19 保持不变。只有压力、温度、粘度等数值是通过曲线拟合从查找表中插值出来的。但在实际应用中，气体往往处于化学和/或热力学非平衡状态，因此必须建立相应的模型。

举例说明，让我们考虑一种由 \(N\) 种不同物质组成的混合气体。对于有限的达姆克勒数（Damköhler number 定义为流动驻留时间与化学反应时间之比），我们必须在模型中加入有限速率的化学反应。它必须描述化学反应导致的组分生成/破坏。在下文中，我们将进一步假设流体动力学和化学反应的时间尺度和空间尺度要比热力学的大得多。因此，我们假设气体在热力学上处于平衡状态，但在化学上处于非平衡状态。为了模拟这种气体混合物的行为，必须在 \(Navier-Stokes\) 方程的基础上增加 \((N - 1)\) 个 \(N\) 种气体的额外传输方程。因此，我们从形式上得到了与公式19 相同的系统，但现在增加了守恒变量 \(W\) 向量、通量向量 \(\vec{F}_C\) 和 \(\vec{F}_V\)，以及由 \((N - 1)\) 个物种方程扩展的源项 \(\vec{Q}\)。回顾表达式 20 至 25，守恒变量向量现在为

\[\vec{W} = \begin{bmatrix} \rho \\ \rho u \\ \rho v \\ \rho w \\ \rho E \\ \rho Y_1 \\ \vdots \\ \rho Y_{N - 1} \end{bmatrix} \tag{32} \]

对流和粘性通量向量转换成

\[\vec{F}_c = \begin{bmatrix} \rho V \\ \rho u V + n_x p \\ \rho v V + n_y p \\ \rho w V + n_z p \\ \rho H V \\ \rho Y_1 V \\ \vdots \\ \rho Y_{N - 1} V \end{bmatrix}, \quad \vec{F}_v = \begin{bmatrix} 0 \\ n_x \tau_{xx}+n_y \tau_{xy}+n_z \tau_{xz}\\ n_x \tau_{yx}+n_y \tau_{yy}+n_z \tau_{yz}\\ n_x \tau_{zx}+n_y \tau_{zy}+n_z \tau_{zz}\\ n_x \Theta_x + n_y \Theta_y + n_z \Theta_z\\ n_x \Phi_{x,1}+n_y \Phi_{y,1}+n_z \Phi_{z,1}\\ \vdots \\ n_x \Phi_{x,N - 1}+n_y \Phi_{y,N - 1}+n_z \Phi_{z,N - 1} \end{bmatrix} \tag{33} \]

其中

\[\begin{align*} \Theta_x &= u\tau_{xx}+v\tau_{xy}+w\tau_{xz}+k\frac{\partial T}{\partial x}+\rho\sum_{m = 1}^{N}h_mD_m\frac{\partial Y_m}{\partial x},\\ \Theta_y &= u\tau_{yx}+v\tau_{yy}+w\tau_{yz}+k\frac{\partial T}{\partial y}+\rho\sum_{m = 1}^{N}h_mD_m\frac{\partial Y_m}{\partial y},\\ \Theta_z &= u\tau_{zx}+v\tau_{zy}+w\tau_{zz}+k\frac{\partial T}{\partial z}+\rho\sum_{m = 1}^{N}h_mD_m\frac{\partial Y_m}{\partial z},\\ \Phi_{x,m} &= \rho D_m\frac{\partial Y_m}{\partial x},\\ \Phi_{y,m} &= \rho D_m\frac{\partial Y_m}{\partial y},\\ \Phi_{z,m} &= \rho D_m\frac{\partial Y_m}{\partial z}. \end{align*} \tag{34} \]

最终，源项变成

\[\vec{Q} = \begin{bmatrix} 0 \\ \rho f_{e,x} \\ \rho f_{e,y} \\ \rho f_{e,z} \\ \rho \vec{f}_e \cdot \vec{v} + \dot{q}_h \\ \dot{s}_1 \\ \vdots \\ \dot{s}_{N - 1} \end{bmatrix} \tag{35} \]

在上述表达式32-35中，\(Y_m\) 分别表示组分 \(m\) 的质量分数，\(h_m\) 表示焓，\(D_m\) 表示有效二元扩散系数。此外，\(\dot s_m\) 是组分 \(m\) 因化学反应而发生的变化率。请注意，混合物的总密度 \(ρ\) 等于各组分密度 \(ρY_m\) 的总和。因此，由于总密度被视为一个独立的量，因此只剩下 \((N - 1)\) 个独立的密度 \(ρYm\)。剩余的质量分数 \(Y_N\) 由以下公式求得

\[Y_N = 1 - \sum_{m = 1}^{N - 1}Y_m \tag{36} \]

为了找到压力 \(p\) 的表达式，我们首先假设各个组分的行为类似于理想气体，即

\[p_m = \rho Y_m \frac{R_u}{W_m} T \tag{37} \]

\(R_u\) 表示通用气体常数，\(W_m\) 表示分子量。结合道尔定律 （Dalton’s law）

\[p = \sum_{m=1}^N p_m \tag{38} \]

可以写成

\[p = \rho R_u T \sum_{m=1}^N \frac{Y_m}{W_m} \tag{39} \]

需要注意的是，由于气体处于热力学平衡状态，所有组分都具有相同的温度 \(T\)。温度必须根据表达式进行迭代计算

\[e = \sum_{m = 1}^{N} \left[ Y_m \left( h_{f,m}^0 + \int_{T_{\text{ref}}}^{T} c_{p,m} \, \mathrm{d}T \right) \right] - \frac{p}{\rho} \tag{40} \]

气体混合物的内能 \(e\) 通过方程6可以获得。方程40中 \(h_{f,m}^0\)，\(c_{p,m}\) 和 \(T_{ref}\) 分别表示热方程，定压比热和第 \(m\) 个组分的参考温度。通过曲线拟合，确定了组分的上述量值以及热导率 \(k\) 和动态粘度 \(μ\) 的值。

最后一部分是公式 35 中的化学源项 \(\dot s_m\)。涉及 \(N\) 个组分的 \(N_R\) 基本反应的速率方程可以写成一般形式

\[\sum_{m = 1}^{N} \nu_{lm}' C_m \underset{K_{\text{b}l}}{\overset{K_{\text{f}l}}{\rightleftharpoons}} \sum_{m = 1}^{N} \nu_{lm}'' C_m \quad \text{for} \quad l = 1,2,\dots,N_R \tag{41} \]

其中，\(v_{lm}'\) 和 \(v_{lm}''\) 分别是第 \(l\) 个正向反应和逆向反应中物质 \(m\) 的化学计量系数（stoichiometric coefficients）。此外，\(C_m\) 表示物质 \(m\) 的摩尔浓度（\(C_m = \rho Y_m / W_m\) ），最后，\(K_{fl}\) 和 \(K_{bl}\) 分别表示第 \(l\) 个反应步骤的正向和逆向反应速率常数。它们由经验阿伦尼乌斯（Arrhenius formulas）公式给出：

\[K_{\mathrm{f}} = A_{\mathrm{f}} T^{B_{\mathrm{f}}} \exp\left(-\frac{E_{\mathrm{f}}}{R_{u}T}\right) \\ K_{\mathrm{b}} = A_{\mathrm{b}} T^{B_{\mathrm{b}}} \exp\left(-\frac{E_{\mathrm{b}}}{R_{u}T}\right) \]

式中，\(A_{\mathrm{f}}\) 和 \(A_{\mathrm{b}}\) 是阿伦尼乌斯系数，\(E_{\mathrm{f}}\) 和 \(E_{\mathrm{b}}\) 表示活化能，\(B_{\mathrm{f}}\) 和 \(B_{\mathrm{b}}\) 分别为常数。第 \(l\) 个反应引起的物质 \(m\) 摩尔浓度的变化率由下式给出 。

\[\dot{C}_{lm} = (v_{lm}'' - v_{lm}') \left( K_{fl} \prod_{n = 1}^{N} C_{n}^{v_{ln}'} - K_{bl} \prod_{n = 1}^{N} C_{n}^{v_{ln}''} \right) \tag{42} \]

因此，结合式(2.42)，我们可以计算出物质 \(m\) 的总变化率：

\[\dot{s}_{m} = W_{m} \sum_{l = 1}^{N_{R}} \dot{C}_{lm} \tag{43} \]

更多细节可查阅上述参考文献。关于化学反应流的控制方程，以及通量的雅可比矩阵及其特征值的详细概述，也可在参考文献[28]中找到。

真实气体的另一个实际例子是蒸汽的模拟，或者在涡轮机械应用中要求更高的湿蒸汽模拟。在后一种情况下，蒸汽与水滴混合，此时我们涉及到多相流。可以通过求解一组额外的输运方程，或者沿着多条流线追踪液滴。这些模拟在现代蒸汽轮机叶栅设计中有着非常重要的应用。例如，对通过涡轮叶片的流动进行分析，有助于理解由凝结引起的超临界激波的产生以及流动不稳定性，这些因素会给叶片带来额外的动态载荷，进而损失效率。

4.3. N-S方程的简化形式

接下来，我们将考虑纳维 - 斯托克斯方程（2.19）的三种常见简化形式。在此，我们将重点关注每种近似背后的物理原理。前两种纳维 - 斯托克斯方程简化形式的方程见附录。

4.3.1. 薄剪切层近似

在模拟高雷诺数下物体绕流时（即边界层相对于特征尺寸较薄的情况），纳维 - 斯托克斯方程（19）可以简化。一个必要条件是不存在大面积的边界层分离。由此可以预示，只有在垂直于物体表面方向（图中的 \(\eta\) 方向）上的流动参量梯度会对粘性应力有贡献 。另一方面，在计算剪切应力张量（式(14)和(15)）时，其他坐标方向（图中的 \(\xi\) 方向）上的梯度可忽略不计。这里我们所说的是纳维 - 斯托克斯方程的所谓薄剪切层（TSL）近似。TSL 修正的目的在于，粘性项的数值计算成本会降低，而且在这些假设条件下，解仍能保持足够的精度。从实际角度来看，TSL 近似也是合理的。

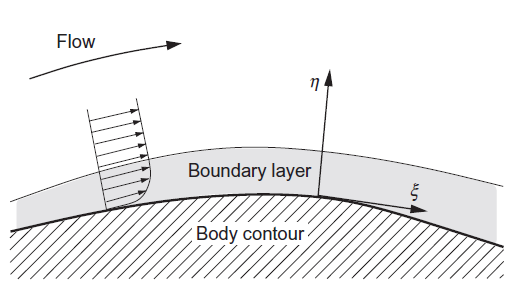
对于高雷诺数的情形，在壁面法向方向上的网格的分别率需要很高，以便于更好的捕捉边界层。出于计算内存的速度的限制，在其他方向上的网格生成较粗的网格。这反过来又导致梯度评估的数值精度大大低于法向方向。由于二次流（如叶片排中的二次流）无法得到适当解决，TSL 简化通常只应用于外部空气动力学。

“secondary flow” 指二次流 ，是因流线弯曲、水流分离等引起的除主流以外的各种次生流动的总称 。像在叶片排（blade row ）中，叶片的形状、布局以及流体绕叶片流动时的复杂相互作用，会使流体在主流方向之外产生额外的流动分量，这就是二次流。比如在叶轮机通道内，由于叶片表面边界层发展、叶片尾迹以及通道内的压力梯度等因素，会诱导出垂直或斜交于主流方向的二次流。二次流会影响流场的压力分布、能量损失以及传热特性等，对设备性能有重要影响 。

4.3.2. Parabolized Navier-Stokes 方程

这种情况下，满足下面三个条件：

• 流动为定常的：守恒变量不随时间变化；
• 流体主要沿一个主方向流动（例如：不能存在边界层分离）；
• 横向流动分量可忽略。

控制方程（19）可以简化为一种称为抛物线纳维 - 斯托克斯（PNS）方程的形式 。上述条件使我们能够在粘性应力项（式(15)）中，将 \(u\)、\(v\) 和 \(w\) 沿流向的导数设为零。此外，粘性应力张量 \(\overline{\tau}\)、其做功项 \(\overline{\tau} \cdot \vec{\nu}\) 以及热传导项 \(k\nabla T\) 在流向的分量，从式(23)的粘性通量矢量中被去除。连续性方程以及对流通量（式(21)）保持不变。考虑图中所示的情形，其中主流方向与 \(x\) 坐标一致，可以证明PNS近似会得到一组抛物型/椭圆型混合方程。即，流向的动量方程与能量方程变为抛物型，因此可以沿 \(x\) 方向推进求解。\(y\) 方向和 \(z\) 方向的动量方程是椭圆型的，需要在每个 \(x\) 平面上迭代求解。因此，PNS方法的主要优势在于极大地降低了流场求解的复杂度——从完整的三维流场变成了一系列的二维问题。

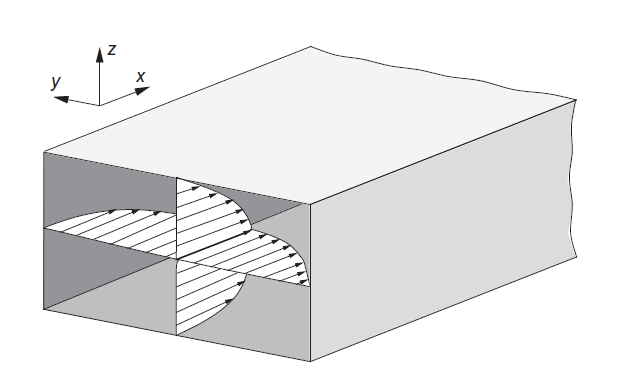
对于抛物线 N-S 方程的典型应用就是管道内部流动，以及使用 space-marching 方法的定常超声速流动模拟。

4.3.3. 欧拉方程

如我们所见，纳维 - 斯托克斯方程描述了粘性流体的行为。在许多情况下，完全忽略粘性效应是一种有效的近似，例如对于高雷诺数流动，此时边界层相较于物体尺寸非常薄。在这种情况下，我们可以简单地从式(19)中省略粘性通量矢量 \(\vec{F}_{\mathrm{v}}\) 。这样，我们就得到：

\[\frac{\partial}{\partial t} \int_{\Omega} \vec{W} \mathrm{d}\Omega + \oint_{\partial\Omega} \vec{F}_{\mathrm{c}} \mathrm{d}S = \int_{\Omega} \vec{Q} \mathrm{d}\Omega. \tag{44} \]

其余各项仍由之前的式(20) - (22)和式(25)给出。这种简化形式的控制方程称为欧拉方程。它们描述了无粘性流体中流动参量的纯对流。如果欧拉方程以守恒形式表述（如上述形式），它们能够精确地描述诸如激波、膨胀波以及三角翼（具有尖锐前缘）上的涡等重要现象。此外，欧拉方程过去一直是——并且现在仍然是——离散化方法和边界条件发展的基础。

然而，需要注意的是，如今由于个人计算机计算能力的提升以及对模拟质量要求的提高，欧拉方程在流动模拟中应用相对较少。