等熵流动

等熵流动

相关书籍中介绍：理想绝热意味着等熵，亦即绝热且可逆，并且只适用于可压缩流动。下面援引NASA关于拉法尔喷管的等熵流动介绍。

当气体被强制通过管道时，气体分子会被管道壁面偏转。如果气体速度远低于其声速，气体密度保持不变，气流速度增加。然而，当气流速度接近声速时，我们必须考虑气体的可压缩性影响。气体密度会随位置变化。

考虑气体流过管道（如图所示），如果气流被非常缓慢地压缩（面积减小），然后再逐渐膨胀（面积增大），气流状态会恢复到初始值。我们称这样的过程是可逆的。从热力学第二定律的角度来看，可逆流动的熵值保持不变。工程师们将这种类型的流动称为等熵流，它是由希腊语 “iso”（相同）和 “entropy”（熵）组合而成。

当流动变量的变化很小且很缓慢时，就会出现等熵流，比如上述理想的通过喷嘴的流动。声波的产生就是一个等熵过程。在流动面积增加的同时转向的超声速流动也是等熵的。由于面积增加，我们称这种情况为等熵膨胀。如果超声速流动突然转向且流动面积减小，就会产生激波，流动变为不可逆。此时等熵关系不再适用，流动由斜激波或正激波关系控制。

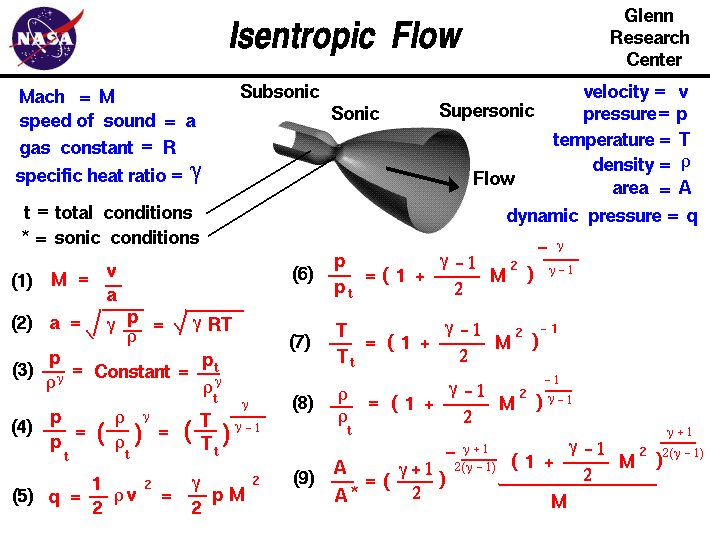
速度 = \(v\)，压力 = \(p\)，温度 = \(T\)，密度 = \(\rho\)，面积 = \(A\)，动压 = \(q\)，马赫数 = \(M\)，声速 = \(a\)，气体常数 = \(R\)，比热比 = \(\gamma\)，* = 临界条件，\(t\) = 总条件

• 公式1

\[M = v / a \]

声速又取决于密度 \(\rho\)、压力 \(p\)、温度 \(T\) 和比热比 \(\gamma\)：

• 公式2

\[a = \sqrt{\gamma \frac{p}{\rho}} = \sqrt{\gamma R T} \]

其中 \(R\) 是状态方程中的气体常数。从气体的熵方程出发，可以推导出等熵流中压力和密度的关系如下：

• 公式3

\[\frac{p}{\rho^{\gamma}} = 常量 \]

我们可以通过定义总条件（即气流等熵静止时的压力和密度）来确定这个常量的值。这些方程中许多带有 “\(t\)” 下标的量表示 “总条件”。（你可能从伯努利方程的相关经验中对总条件已经有了一些概念 ）。

\[\frac{p}{\rho^{\gamma}} = 常量 = \frac{p_{t}}{\rho_{t}^{\gamma}} \]

利用状态方程，我们可以很容易地从公式(3)推导出以下关系：

• 公式4

\[\frac{p}{p_{t}} = (\frac{\rho}{\rho_{t}})^{\gamma} = (\frac{T}{T_{t}})^{\frac{\gamma}{\gamma - 1}} \]

动压 \(q\) 的定义为：

• 公式5

\[q = \frac{\rho v^{2}}{2} = \frac{\gamma p M^{2}}{2} \]

利用质量、动量和能量守恒定律以及气流中总焓的定义，我们可以推导出以下关系：

• 公式6

\[\frac{p}{p_{t}} = [1 + \frac{M^{2}(\gamma - 1)}{2}]^{-\frac{\gamma}{\gamma - 1}} \]

• 公式7

\[\frac{T}{T_{t}} = [1 + \frac{M^{2}(\gamma - 1)}{2}]^{-1} \]

• 公式8

\[\frac{\rho}{\rho_{t}} = [1 + \frac{M^{2}(\gamma - 1)}{2}]^{-\frac{1}{\gamma - 1}} \]

然后，考虑可压缩质量流量方程，我们可以推导出：

• 公式9

\[\frac{A}{A^{*}} = \frac{\left[1 + \frac{M^{2}(\gamma - 1)}{2}\right]^{\frac{\gamma + 1}{2(\gamma - 1)}}\left(\frac{\gamma + 1}{2}\right)^{-\frac{\gamma + 1}{2(\gamma - 1)}}}{M} \]

带星号的条件表示气流壅塞时的情况，此时马赫数等于1。注意马赫数在本页面右侧所有方程中都起着重要作用。如果确定了气流的马赫数，就可以确定所有其他的流动关系。同样，确定任何一个流动关系（例如压力比），就能确定马赫数，并设定所有其他的流动条件。

比热比

1. 热力学

热力学是物理学的一个分支，主要研究系统的能量和功。热力学只关注系统的宏观响应，这些响应是我们在实验中能够观察和测量的。在火箭科学领域，我们对热力学在发动机设计和高速飞行中所发挥的作用尤为关注。

2. 比热容

在本页面，我们将推导一些方程，这些方程把气体的热容与状态方程中使用的气体常数联系起来。我们会用到状态变量的“比”值。对于科学家而言，一个“比”状态变量指的是该变量的值除以物质的质量。这样一来，我们在推导变量之间的关系时，就无需考虑物质的具体数量。

在任何时候，我们都可以将比变量乘以物质的量，从而得到流动变量的实际值。通过对热传递的学习，我们知道两个物体之间传递的热量与物体之间的温差以及物体的热容成正比。

热容是一个常数，它表示单位温度升高时所添加的热量。这个常数的值因材料不同而有所差异，并且取决于具体的过程。比热容不是一个状态变量而是一个过程变量。在热力学和统计物理中，通常研究定压比热和定容比热。

3. 焓方程

在处理气体问题时，使用基于气体焓的热力学方程形式最为方便。根据焓的定义：

\[h = e + pv \]

其中，\(h\)是比焓，\(p\)是压力，\(v\)是比体积，\(e\)是比内能。在一个过程中，这些变量的值会发生变化。我们用希腊字母\(\Delta\)（德尔塔）来表示这种变化。所以，“\(\Delta h\)”表示在一个过程中，“\(h\)”从状态1到状态2的变化量。那么，对于一个定压过程，焓方程变为：

\[\Delta h = \Delta e + p\Delta v \]

焓、内能和体积都发生了变化，但压力保持不变。从我们对焓方程的推导可知，在定压过程中，比焓的变化量等于热传递：

\[\Delta h = c_p\Delta T \]

其中，\(\Delta T\)是过程中气体的温度变化量，\(c_p\)是比热容。我们给比热容加上下标“\(p\)”，以提醒我们这个值仅适用于定压过程。

气体的状态方程通过气体常数\(R\)将温度、压力和体积联系起来。航空学家使用的气体常数是由通用气体常数推导而来的，但每种气体都有其独特的值。

\[pv = RT \]

如果是定压过程，那么：

\[p\Delta v = R\Delta T \]

现在，假设我们对气体进行一个定容过程，使其产生与我们一直在讨论的定压过程完全相同的温度变化。根据热力学第一定律：

\[\Delta e = \Delta q - \Delta w \]

其中，\(q\)是比热传递，\(w\)是气体所做的功。对于定容过程，功等于零。我们可以将热传递表示为一个常数乘以温度变化量，即：

\[\Delta e = c_v\Delta T \]

其中，\(\Delta T\)是过程中气体的温度变化量，\(c_v\)是比热容。我们给比热容加上下标“\(v\)”，以提醒我们这个值仅适用于定容过程。尽管这个过程和定压过程的温度变化相同，但比热容的值是不同的。

由于我们选择的定容过程与定压过程具有相同的温度变化，所以可以将上面给出的“\(\Delta e\)”的表达式代入焓方程。一般情况下，不能进行这样的代换，因为定压过程和定容过程会产生不同的温度变化。如果我们将“\(\Delta e\)”“\(p\Delta v\)”和“\(\Delta h\)”的表达式代入焓方程，可得：

\[c_p\Delta T = c_v\Delta T + R\Delta T \]

两边同时除以“\(\Delta T\)”，得到关系式：

\[c_p = c_v + R \]

定压和定容过程的比热常数与给定气体的气体常数相关。这个相当了不起的结果是从热力学关系推导出来的，而这些热力学关系是基于对物理系统和过程的观察。利用气体动理论，从分子层面的能量守恒角度也可以推导出相同的结果。

我们可以定义一个额外的变量，称为比热比，用希腊字母“\(\gamma\)”表示，它等于\(c_p\)除以\(c_v\)：

\[\gamma = \frac{c_p}{c_v} \]

“\(\gamma\)”只是一个数值，其大小取决于气体的状态。在标准日条件下，空气的\(\gamma = 1.4\)。“\(\gamma\)”出现在许多流体方程中，包括简单压缩或膨胀过程中压力、温度和体积的关系式、声速方程，以及所有等熵流和激波的方程。由于“\(\gamma\)”的值仅取决于气体的状态，因此有针对特定气体的\(\gamma\)值表。你可以使用这些表格来解决气体动力学问题。