Bernoulli Equation

伯努利方程

1. 方程形式

伯努利方程并非一个独立的定律，而是在不同条件下由 Navier-Stokes 动量方程（式（1））和能量方程（式（2））推导而来的。

\[\rho\left(\frac{\partial u_{j}}{\partial t} + u_{i}\frac{\partial u_{j}}{\partial x_{i}}\right)=-\frac{\partial p}{\partial x_{j}}+\rho g_{j}+\frac{\partial}{\partial x_{i}}\left[\mu\left(\frac{\partial u_{j}}{\partial x_{i}}+\frac{\partial u_{i}}{\partial x_{j}}\right)+\left(\mu_{v}-\frac{2}{3}\mu\right)\frac{\partial u_{m}}{\partial x_{m}}\delta_{ij}\right] \tag{1} \]

\[\rho\frac{De}{Dt}=-p\frac{\partial u_{m}}{\partial x_{m}} + 2\mu\left(S_{ij}-\frac{1}{3}\frac{\partial u_{m}}{\partial x_{m}}\delta_{ij}\right)^{2}+\mu_{v}\left(\frac{\partial u_{m}}{\partial x_{m}}\right)^{2}+\frac{\partial}{\partial x_{i}}\left(k\frac{\partial T}{\partial x_{i}}\right) \tag{2} \]

首先推导出由动能方程简化而来的伯努利方程形式，考虑无粘流动时\(\mu = \mu_v = 0\)，重力是唯一的体积力，因此式1就简化为欧拉方程

\[\frac{\partial u_{j}}{\partial t}+u_{i}\frac{\partial u_{j}}{\partial x_{i}}=-\frac{1}{\rho}\frac{\partial p}{\partial x_{j}}-\frac{\partial \varPhi}{\partial x_{j}} \tag{3} \]

式中：\(\varPhi = gz\) 表示体积势函数；\(g\)为重力加速度；z轴为垂直方向，如果流动是正压流动，那么\(\rho = \rho(p)\)，并且：

\[\frac{1}{\rho}\frac{\partial p}{\partial x_j}=\frac{\partial }{\partial x_j}\int_{p_0}^{p}\frac{dp'}{\rho(p')} \tag{4} \]

式中，\(dp/\rho\)是全微分，\(p_0\)是参考压力，\(p'\)是积分变量。在上式中，积分置于端点有关，而与积分路径无关。流体的质点在运动的过程中，它的密度只是压强的函数而和其他热力学变数（如温度）无关，则称此流体为正压流体，对应流动为正压流动（barotropic），其中不可压缩流体和理想绝热（等熵）气体都是正压流体 。

除此之外式3中对流加速度可以改写成速度-涡量的向量积和单位质量动能梯度的形式

\[u_{i}\frac{\partial u_{j}}{\partial x_{i}}=-(\mathbf{u} \times \boldsymbol{\omega})_{j}+\frac{\partial}{\partial x_{j}}\left(\frac{1}{2}u_{i}^{2}\right) \tag{5} \]

将式（5）和式（4）带入到式（3）中：

\[\frac{\partial u_{j}}{\partial t}+\frac{\partial }{\partial x_{j}}\left[\frac{1}{2}u_{i}^{2}+\int_{p_0}^{p}\frac{dp'}{\rho(p')}+gz\right]=(\mathbf{u} \times \boldsymbol{\omega})_{j} \tag{6} \]

所有的梯度项都被合并成了伯努利函数B，即中括号中的内容。式（6）可以用于推导无粘正压流动伯努利方程的演化。

首先考虑定常流动（\(\partial u_j/\partial t = 0\)），这样式（6）简化成

\[\nabla B=\mathbf{u}\times\boldsymbol{\omega} \tag{7} \]

左端项是正交于常数曲面B的向量，右端项是同时垂直于\(\boldsymbol{u}\)和\(\boldsymbol{\omega}\)的向量。如图所示，

这是一个由流线和涡线定义的曲面，在该曲面上，伯努利函数是一个常量，注意流线和涡线可以为任一方位。

由此可知B为常数的曲面必定包含流线和涡线，因此，无粘、定常、正压流动满足：

\[\frac{1}{2}u_{i}^{2}+\int_{p_0}^{p}\frac{dp'}{\rho(p')}+gz = 沿流线和涡线为常数值 \tag{8} \]

这是伯努利几种可能方程的第一种形式，另外，如果流动无旋（\(\omega = 0\)） 的，那么式（7）就有

\[\frac{1}{2}u_{i}^{2}+\int_{p_0}^{p}\frac{dp'}{\rho(p')}+gz=\text{constant everywhere} \tag{9} \]

可以证明，存在包含流线和涡线的曲面的充分条件是流动为正压流动，顺便说一下，这种类型的曲面称为 Lamb surfaces ，是为了纪念杰出的英国应用数学家和流体力学家霍勒斯・兰姆。

在一般的非正压流动中，可以在流场中的任意两点之间绘制由流线和涡线段组成的路径。那么式（8）是有效的，条件是在所选的特定路径上计算积分。如前文所述，（式（8）要求流动是定常的、无粘性的，并且只有重力（或其他保守）体积力作用于其上。

我们在此仅指出一个要点：在非旋转参考系中，如果粘性效应可以忽略不计，正压无旋流动将保持无旋。考虑绕固体物体的流动，比如翼型（如图所示）。

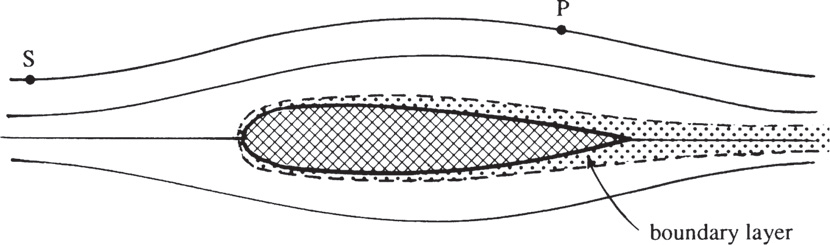
在靠近物体表面的薄粘性层（称为边界层）之外的所有点处，流动都是无旋的。这是因为在粘性层之外的流线上的粒子 P 从某点 S 出发，在 S 点处流动是均匀的，因此是无旋的。所以，在这个例子中，伯努利方程式（9）在粘性层之外的所有地方都成立。

---

下面介绍由不考虑粘性剪切力以及热交换（\(\sigma_{ij} = q_i = 0\)）的能量方程（式（2））推导而来的伯努利方程形式，针对定常流动（\(\partial / \partial t = 0\)）:

\[\rho u_{i}\frac{\partial }{\partial x_{i}}\left(e + \frac{1}{2}u_{j}^{2}\right)=\rho u_{i}g_{i}-\frac{\partial }{\partial x_{j}}(\rho u_{j}p/\rho) \tag{10} \]

当体积力是具有势函数\(gz\)的保守力，定常连续性方程\(\partial (\rho u_i) / \partial x_i = 0\)用于简化式（10），上式就变成：

\[\rho u_{i}\frac{\partial}{\partial x_{i}}\left(e + \frac{p}{\rho}+\frac{1}{2}u_{j}^{2}+gz\right)=0 \tag{11} \]

已知\(h = e + \frac{p}{\rho}\) ，所以表明\(h + \frac{|\boldsymbol{u}|^2}{2} + gz\)必须正交于当地的流线方向\(u_i\)，因此，另一种伯努利方程形式为：

\[h+\frac{1}{2}|\mathbf{u}|^{2}+gz=\text{constant on streamlines} \tag{12} \]

能量方程经傅里叶热传导定律转换后：

\[\frac{Ds}{Dt} = \frac{1}{\rho}\frac{\partial}{\partial x_{i}}\left(\frac{k}{T}\frac{\partial T}{\partial x_{i}}\right)+\frac{k}{\rho T^{2}}\left(\frac{\partial T}{\partial x_{i}}\right)^{2}+\frac{\varepsilon}{T} \tag{13} \]

上述方程，等式的右端第一项表示由热传导导致的熵增或熵减，后面两项与温度和速度梯度的平方成正比，代表了热传导和粘性生热所导致的熵产生。热力学第二定律表明由不可逆现象引起的熵产生为正值，因此（动力粘度、热扩散率、热导率）\(\mu,\kappa,k>0\)。因此，在大多数流体流动分析中，无需明确援引热力学第二定律，因为通过取粘度和热导率的正值，该定律已得到满足。此外，式（13）要求，当流动为无粘性且不导热时，即当\(Ds/Dt=0\)时，流体微团的熵应沿其运动轨迹保持不变。

所以，无粘、无热传递的流动是等熵流动（熵\(s\)沿粒子运动轨迹不变），并且当熵\(s\)为常数时，意味着\(dp/\rho = dh\)。因此只有动量伯努利方程式（8）、（9）中忽略热传导和粘性应力时，路径积分\(\int \frac{dp}{\rho}\)才仅仅是端点的函数\(h\)。式（12）在高速气流的情况下非常有用，因为在高速气流中，沿流线方向动能和热能之间存在显著的相互作用，该式与式（8）基本一样，但不包含式（8）考虑正压流动和沿涡线计算的情况。

总结：当前至少有四种伯努利方程形式

• 无粘、定常、正压流动：式（8）
• 无粘、无旋、非定常、正压流动：

\[\frac{\partial \phi}{\partial t}+\frac{1}{2}|\nabla\phi|^{2}+\int_{p_0}^{p}\frac{dp'}{\rho(p')}+gz = \text{constant} \tag{14} \]

• 无粘、等熵、定常流动：式（12）
• 粘度恒定、无旋、非定常、常密度流动：

\[\int_{1}^{2}\frac{\partial \mathbf{u}}{\partial t}\cdot d\mathbf{s}+\left(\frac{1}{2}|\mathbf{u}|^{2}+gz + \frac{p}{\rho}\right)_2=\left(\frac{1}{2}|\mathbf{u}|^{2}+gz+\frac{p}{\rho}\right)_1 \tag{15} \]

式（15）中脚标1、2分别表示同一时刻同一流线的上、下游位置

\[\frac{\partial \phi}{\partial t}+\frac{1}{2}|\nabla\phi|^{2}+gz+\frac{p}{\rho}=\text{constant} \tag{16} \]

2. 伯努利方程的应用

2.1 皮托管

首先来考虑一种简单的用于测量流体流中局部流速的装置，方法是插入一根细弯管，如图所示，这种弯管被称为皮托管，得名于法国数学家亨利·皮托（1695 - 1771 年），他曾使用一根弯曲的玻璃管来测量塞纳河的流速。考虑处于同一高度的两个点（点1和点2），点1远离该弯管，点2恰好在开口端的正前方，此处流体速度\(u_{2}\)为零。

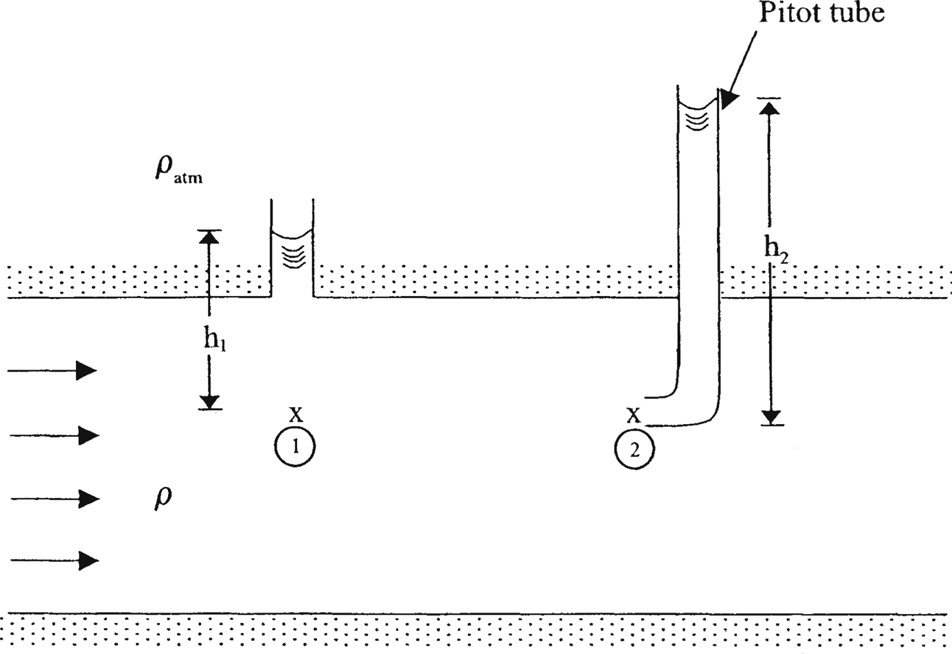
如果流动沿连接1和2的流线是定常、无旋且常密度的，那么下式就变成：

\[\begin{aligned} \frac{1}{2}U^{2}+gz + p/\rho&=\text{ a constant along a streamline} \\ \frac{p_1}{\rho}+\frac{1}{2}|\mathbf{u}|_1^{2}&=\frac{p_2}{\rho}+\frac{1}{2}|\mathbf{u}|_2^{2}=\frac{p_2}{\rho} \end{aligned} \tag{17} \]

由此可得出：\(|\mathbf{u}|_1 = \sqrt{2(p_2 - p_1)/\rho}\)，两点处的压力可根据流体静力学平衡得出：\(p_1 = \rho g h_1 \text{ and } p_2 = \rho g h_2\)，因此\(|\mathbf{u}|_1=\sqrt{2g(h_2 - h_1)}\)。

由于假定流体密度远大于皮托管所暴露的大气的密度，因此假定两液柱顶部的压力相同。实际上，它们的差值为\(\rho_{atm}g(h_2 - h_1)\)。当1号位置与壁面之间的流线是直且平行的时候，那么在1号位置以上的区域使用流体静力学近似是可以的。

由皮托管测得的压力\(p_2\)称为滞止压力（Stagnation Pressure）或者总压（Total Pressure），大于当地的静压值。即使没有皮托管来测量滞止压力，通常也会将\(p+\rho \frac{|\mathbf u|^2}{2}\)的局部值称为局部滞止压力，其定义为假设局部流体无摩擦地减速至零速度时所达到的压力。量\(\frac{\rho u^2}{2}\)有时被称为动压力；滞止压力是静压力和动压力之和。

2.2 水箱开孔流动

作为伯努利方程的另一个应用实例，考虑流体通过水箱上的孔口或开口的流动。由于水箱内水位下降，流动略有非定常性，但如果水箱面积远大于孔口面积，这种影响就很小。在远离水箱壁面的任何地方，粘性效应都可以忽略不计。所有流线都可以追溯到水箱中的自由液面，在自由液面上，它们具有相同的伯努利常数\(B = |\mathbf{u}|^{2}/2 + p/\rho + gz\)。由此可知，该流动是无旋的，并且\(B\)在整个流动中保持恒定。

我们希望在水箱自由液面上的一点和射流中的一点之间应用伯努利方程。然而，开口处（图中的A 截面）的情况并不简单，因为射流截面上的压力并不均匀。尽管在射流自由液面上的任何地方，压力都等于大气压力（忽略表面张力的微小影响），但在这个截面处，射流内部的压力并不等于大气压力。由于孔口处的流线是弯曲的，为了平衡离心力，压力必须在射流宽度上发生变化。孔口处（A截面）的压力分布如图所示。然而，射流中的流线在离孔口很短的距离后就变得平行（图中的C截面），此时射流面积小于孔口面积。C截面上的压力是均匀的，且等于大气压力(\(p_{atm}\))，因为在射流表面压力就是这个值。

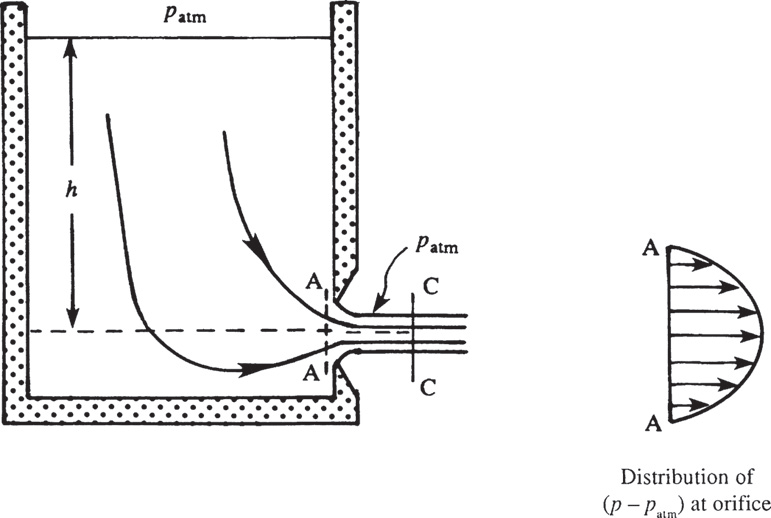
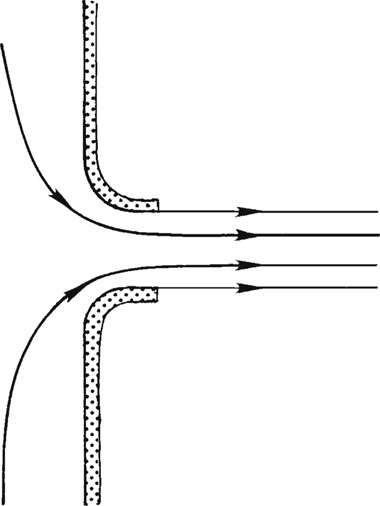
流经圆形孔口，在这里，压力和速度可以在水箱内实现平行流出，因此水箱外的射流宽度不会发生变化。

对于自由液面上的一点与水箱出口C截面上的一点之间的定常、常密度流动应用伯努利方程

\[\frac{p_{atm}}{\rho}+gh=\frac{p_{atm}}{\rho}+\frac{u^{2}}{2} \tag{18} \]

喷口平均速度\(u = \sqrt{2gh}\)，该式指出势能的减少量=动能的增加量，那么质量流量近似为\(\dot m = \rho A_c u = \rho A_c \sqrt{2gh}\)。
\(A_c\)是喷口截面积：

• 对于尖锐边缘孔口，由于射流在孔口下游收缩，则\(A_c\)约为孔口面积的\(62\%\)；
• 对于边缘圆滑的孔口，射流不收缩，出口流线平行，出口压力均匀且等于大气压力，此时A等于孔口的面积。

2.3 忽略重力的常密度流动

当流速为0时，不可压缩流动N-S动量方程简化为流体静压\(p_s\)和作用在静密度\(\rho_s\)上定常体积力之间的平衡

\[0 = -\nabla p_s+\rho_s \mathbf{g} \tag{19} \]

上式等同于\(dp/dz = -\rho g\)，当从下式中减去这种静平衡后，就会有相对流体静压的压力差：\(p'=p-p_s\)，以及静密度差\(\rho ' = \rho -\rho_s\)

\[\begin{aligned} \rho\frac{D\mathbf{u}}{Dt}&=-\nabla p + \rho\mathbf{g}+\mu\nabla^{2}\mathbf{u}\text{ (incompressible)} \\ \tag{20} \rho\frac{D\mathbf{u}}{Dt}&= -\nabla p'+\rho' \mathbf{g}+\mu\nabla^{2}\mathbf{u} \end{aligned} \]

当流体密度是常数时，那么\(\rho ' = 0\)，那么重力体积力项去除后

\[\rho\frac{D\mathbf{u}}{Dt}= -\nabla p'+\mu\nabla^{2}\mathbf{u} \tag{21} \]

正因如此，在常密度流动中定常体积力（像重力）通常在动量方程中会被省略，压力则是相对于局部静压值来衡量的，此外，在这种情况下，\(p'\)中的\('\)通常也会省略。然而，当流动包含自由液面时、流体-流体交界面处密度发生变化时或者其他密度发生变化的情形，重力体积力会重新出现。