多相流模型

目录

• Fluent 中的多相流模型
  • 1. 多相流模型的设置步骤
  • 2. 功能窗口
    • 2.1. 多相流模型的功能窗口
      • 2.1.1. VOF 模型
        • （1）Volume Fraction Formulation
        • （2）Interface Modeling
        • （3）针对体积分数的空间离散方案选择
        • （4）Couple Level-set + VOF
        • （5）Open Channel flow
        • （6）主相和次相的选择
        • （7）相间作用力

Fluent 中的多相流模型

1. 多相流模型的设置步骤

首先是需要设置双精度求解——Double Precision

• 启用多相流模型：VOF、Mixture、Eulerian 三种模型可供选择，求解的复杂度依次增加，其中 VOF、Eulerian 模型需要指定体积分数——Volume Fraction 求解方案；

• 在材料库中选择不同相的材料。如果多相流模型中的流动为可压缩流动：

  • 软件中可以允许使用的流体密度计算方法有：

    • 任意入口边界可以使用多种可压缩理想气体相和/或者不可压缩/可压缩液体；
    • 任意入口边界可使用单个真实气体或者真是液体；
    • 一个入口边界可以使用多种真实气体模型；
    • 多种可压缩液体的使用，可以使用 Fluent 中内置的基于 Tait law 的可压缩液体模型，也可以使用 UDF 来定义。

    对于多种可压缩相，针对可压缩流动的基本方程保持一样，然而边界条件需要修正以考虑由于可压缩流动混合物导致的材料属性的改变。

  • 在理想气体和实际气体混合的情况下，不能使用同一个入口边界，需要分别指定；

  • 当采用 VOF 模型时，若首相为可压缩理想气体，则稳定性提高；

  • 如果指定边界(例如，对于压力入口或者 Intake Fan)处的总压，Fluent 将使用该边界上所指定的温度值作为可压缩相的总温，并将其作为不可压缩相的静温；

  • 对于每个质量流量入口——Mass-flow Inlet，需要为每个单独的相指定质量流量或质量通量。

  (1) 增强的可压缩流动数值方案：由于显式处理了考虑密度变化的源项，可压缩流模拟可能存在收敛困难的问题，在压力和温度变化较大的情况下，这些模拟可能变得极不稳定。在 Ansys Fluent 中，默认启用了一个增强的数值处理，可以在求解开始时和计算可压缩流动期间提供更好的稳定性。该处理控制了每个迭代步之间压力和温度的变化率，并为方程组矩阵提供了额外的对角优势。
  虽然不建议禁用增强的数值处理，但可以使用下面的文本用户界面命令暂时关闭它来研究不稳定的情况：

  solve/set/multiphase-numerics/compressible-flow/enhanced-numerics
  ...
  enhanced compressible flow numerics? [yes] no
  

  (2) 替代的可压缩流动数值方案：对于可压缩多相流的更一般的处理方法是在入口边界对可压缩相进行严格的数学处理。该公式不将进入求解域中的不可压缩和可压缩相视为伪混合物，而是基于基本热力学关系(如 Maxwell 关系)来处理。这种方法涉及到对性质导数的评估，可以通过数值计算或通过解析表达式计算。可以通过文本命令启用这种替代处理：

  solve/set/multiphase-numerics/compressible-flow/alternate-bc-formulation
  alternate compressible bc formulation? [no] y
  use analytical thermodynamic derivatives? [no] y
  

• 定义相的参数，并指定它们之间出现的任何相互作用(例如, 当使用 VOF 模型时, 表面张力系数；当使用混合物模型时，滑移速度函数；当使用欧拉模型时，阻力函数)。

• 针对欧拉多相流模型，如果流动是湍流流动，需要定义多相流湍流模型。

• 如果包含体力，启用重力选项并指定重力加速度。

• 设置边界条件，在设置流动边界时要设置第二相的体积分数，另外，如果在 VOF 模拟中使用了壁面附着力（Wall Adhesion）选项，需要在壁面边界条件中指定接触角度。

• 设置方法和控制条件，并对第二相的体积分数进行针对性的初始化，初始化方法是针对某个特定区域，Patch 该区域中该相的体积分数为指定的值。

2. 功能窗口

2.1. 多相流模型的功能窗口

2.1.1. VOF 模型

（1）Volume Fraction Formulation

体积分数求解方程包括 显示方法 和 隐式方法：

• 显示方法：属于非迭代性的并且与时间相关的，因此只能基于瞬态进行求解。相较于隐式方法求解其具有更高的数值计算精度，但是时间步长受限于基于库朗特数的稳定性准则。

优点：方法的建立和编程相对简单；
缺点：为保证求解的稳定性，步长大小受限，收敛时间长。

• 隐式方法：隐式方法属于迭代性的，并且可以基于稳态和瞬态两种方案求解。隐式方法非常适合稳态求解，相较于显示方法求解，其解信息的传播速度要快很多，其库朗特数可以很大。

优点：用很大的时间步长也可以保证求解的稳定性，减少求解时间；
缺点：方法建立和编程复杂。

对于定常流动问题，到底是使用稳态模拟还是瞬态模拟，取决于流动的特征：

• 稳态模拟：如果稳态解不受初始流动条件影响，并且每一相都有一个单独的入口边界；
• 瞬态模拟：如果稳态解依赖于初始流动条件，并且/或者每一相都没有单独的入口边界。

对于瞬态模拟，隐式方法求解可以使用比显示方法更大的时间步，这是因为 隐式方法的无条件稳定性。然而，隐式时间步长可能会受限于截断误差。当使用一阶瞬态方法时，隐式方法相比显式方法会产生更多的数值耗散。因此 隐式方法应该与更高阶的瞬态方法一起使用来获得更高的计算精度。

稳态与瞬态：研究雨滴从高空落下是否会砸死人的问题，雨滴从某一高度落下，受重力作用速度逐渐加快，加速的同时阻力也在增加，气动阻力与速度的平方成正比，突然某一时刻，阻力与重力相同，此时雨滴将匀速下落。雨滴下落的过程中，如果研究速度，在匀速之前的过程属于瞬态问题，因为该过程中速度随时间的增加而变化；如果研究匀速后的过程，速度不发生变化，在任意时刻下速度都是相同的，因此属于稳态问题。瞬态与稳态的选择与某一物理过程中所研究的物理量是否随时间变化来确定。所有的工程问题都可以用瞬态进行求解，但不一定都能按照稳态求解，稳态只是瞬态的一种简化。

在进行瞬态模拟时，每个时间步内的求解都是假定为稳态进行求解的。稳态求解与初始值无关，瞬态求解与初始值相关。稳态求解中，好的初始值选取有利于收敛。

（2）Interface Modeling

该选项适用于所有的多相流模型，在求解多相流问题之前需要指定 Interface 处理方法，不同的处理方法对应不同的体积分数离散方案。主要的类型有：

• Sharp：在不同的相之间具有明显的 Interface 时使用；

  • Interfacial Anti-Diffusion

    针对在 Interaface 处的单元，防止其之间出现渗透的现象，仍保持明显的交界面。同时尝试去抑制由体积分数对流格式所产生的数值耗散，这种数值耗散会影响收敛，尤其是设置的参数跨越太大导致求解不稳定、较大的时间步长。一般用于粗网格，或者具有高纵横比的网格，在相的交界面处单元体积过渡比较大的情况。对于 Interfacial Anti-Diffusion 处理方法的力度可以通过 TUI 命令行设置一个 0 ~ 1 的值：define/models/multiphase/interface-modeling-options。

    该处理方法如果强度过高会导致人工波（Artifical waves）的出现，物极必反。此时可以通过开启动态调整反扩散强度的方案来避免人工波的产生。该方案是通过降低交界面切向的 Anti-Diffusion 强度来实现的：

    solve/set/multiphase-numerics/advanced-stability-controls/anti-diffusion/
    enable-dynamic-strength?
    
    solve/set/multiphase-numerics/advanced-stability-controls/anti-diffusion/enable-dynamic-strength?
    Enable anti-diffusion treatment with dynamic strength? [no] yes
    

    动态调整反扩散的原理是：

\[ \begin{cases} C = min\left [ (cos \theta)^m, C_{max}\right] \tag{1} \\ cos \theta = |\hat{n} \cdot \hat{A}| \\ \end{cases} \]

式中：\(C\)为反扩散强度；\(\hat{n}\)为交界面单位法向量；\(\hat{A}\) 面积单位法向量；\(\theta\) 面积与交界面单元法向量之间的夹角；\(m\) 是指数，默认值为 1.5；\(C_{max}\) 表示反扩散强度的最大值，介于 0 ~ 0.95 之间，默认值为 0.75。

其中指数 \(m\) 和最大反扩散强度 \(C_{max}\) 的值可以通过下面的 TUI 命令修改：

	```
	#指数m
	solve/set/multiphase-numerics/advanced-stability-controls/anti-diffusion/
	set-dynamic-strength-exponent
	#反扩散强度C_max
	solve/set/multiphase-numerics/advanced-stability-controls/anti-diffusion/
	set-maximum-dynamic-strength
	```

• Dispersed：适用于流体之间互相渗透，即分散的，没有明显的交界面；

• Sharp/Dispersed：这是一种混合方法，适用于不同的相之间既没有太明显的交界面又并不是完全渗透的情况。

  • Interface Modeling Options

    

    

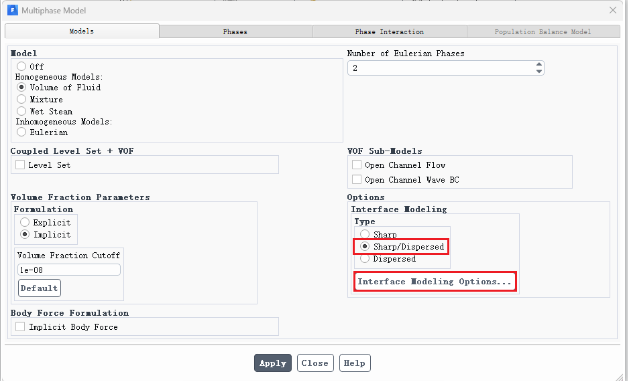
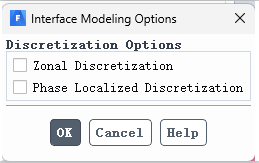
    具有两个选项：第一个选项是基于单元区域来求解交界面是 sharp/dispersed 类型的多相流问题；第二个选项是基于成对的相在交界面区域出的处理方法。

    勾选第一个选项时，需在 Fluid zone 设置 slope limiter：

    

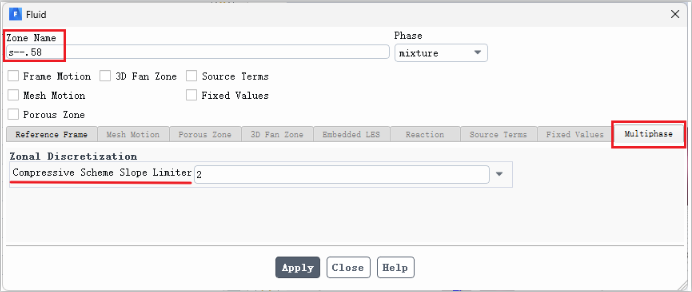
    勾选第二个选项时，需要在多相流模型中选择：

    

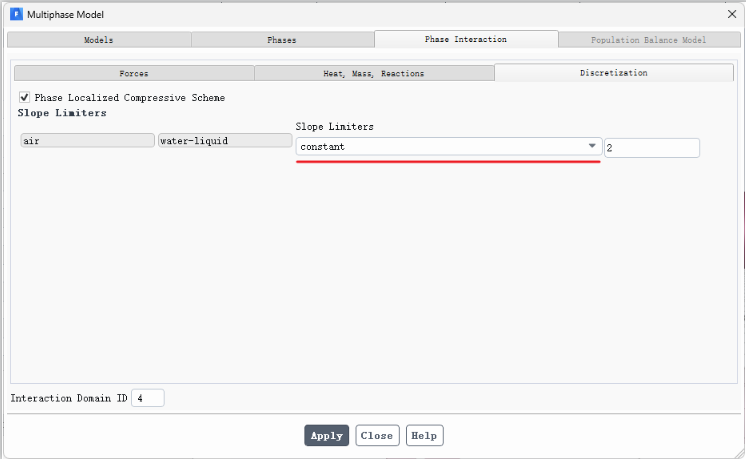
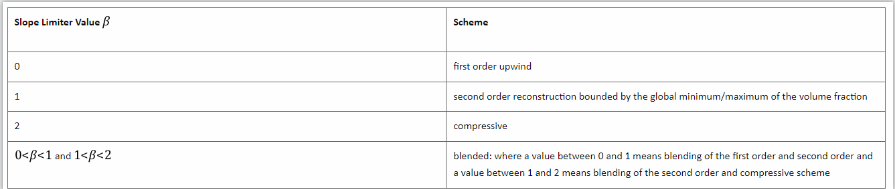
    • Slope Limiters

      适用于高阶离散方案的一种修正方法，避免高阶空间离散化方案因求解域急剧变化而产生的虚假振荡或摆动，该值需要设置在 0 ~ 1 之间：

      

（3）针对体积分数的空间离散方案选择

根据不同的边界处理方式、计算体积分数的数值方法，对应的空间离散方案有：

Interface Modeling Type	隐式方法	显式方法
Sharp	Compressive / BGM(仅限于定常) / Modified HRIC	Geo-Reconstruct / CICSAM / Compressive / Modified HRIC
Sharp/Dispersed	Compressive / Modified HRIC	同左
Dispersed	First Order Upwind Second Order Upwind QUICK	First Order Upwind QUICK

CICSAM 是一种高分辨率差分格式，适用于不同相之间高粘度比的流动，其优点是具有与几何重构方案一样的效果。

（4）Couple Level-set + VOF

该方法是同时兼顾了Level-set 方法和VOF方法优势的一种混合方法。

• Level-set方法适合解决两相交界面拓扑较为复杂的问题，也是常用的Interface Tracking 方法。类似于VOF模型中的Interface Tracking方法，该方法使用Level-set函数捕捉和跟踪两相交界面，该函数被定义为与交界面的有符号距离（距离分正负）。因为Level-set函数是光滑且连续的，所以可以准确计算空间梯度。反过来说，也可以准确预测由于曲率导致的交界面曲率和表面张力。但是，Level-set方法无法保证体积守恒。

• VOF方法是保证体积守恒的（naturally volume-conserved），因为它计算和Tracking的是每个单元/控制体中特定相位的体积分数而不是 Interface本身。但是VOF方法的缺点在于其空间导数的计算，因为VOF函数中对特定相的体积分数计算在Interface处是不连续的。

  Couple Level-set VOF模型是专门为不涉及传质的两相流动而设计的，且仅适用于求解瞬态问题。针对网格类型要求，二维网格只能是四边形、三角形或者两者混合类型的网格；三维网格只能是六面体、四面体或者两者混合类型的网格。

开启该混合方法后，关于体积分数的空间离散方案推荐选用几何重构方案（Geo-Reconstruce Scheme）。

（5）Open Channel flow

该流动模型为VOF的子模型，其为明渠流动。该种流动是由重力作为驱动力，因此使用该模型之前要打开重力选项。明渠流动是具有自由面的流动，自由面上各点的压强为大气压，其相对压强为0，所以明渠流动又称为无压流动。

比如：人工渠道、天然河道以及非满管流管道的流动。

（6）主相和次相的选择

所研究的流动状态下，体积分数占比最高的那一相，且为连续相，比如水在管道中流动，那么水就是连续相，空气可能会以气泡的形式存在于水中，作为分散相存在，因此此时水为第一相，空气为第二相。

（7）相间作用力

表面张力效应的重要程度是基于两个无量纲量的值来确定的：雷诺数（\(Re\)）和毛细管数（\(Ca\)）；或者雷诺数（\(Re\)）和韦伯数（\(We\)）。当\(Re \ll 1\)时，我们关注的量是毛细管数：

\[Ca = \frac{\mu U}{\sigma} \tag{5} \]

而当\(Re \gg 1\)时，我们关注的量是韦伯数：

\[We = \frac{\rho LU^{2}}{\sigma} \tag{6} \]

其中，\(U\)是自由流速度。如果\(Ca \gg 1\) 或者 \(We \gg 1\)，表面张力效应可以忽略不计。

若要在模型中考虑表面张力的影响，请参考《用户指南》中的“考虑表面张力和粘附效应”部分。

通过韦伯数 We先判断惯性力与表面张力之比,如果\(We >> 1\)，则可忽略表面张力的作用，如果比值很小，那么就需要考虑表面张力的作用，此时需要开启表面张力模型（Surface Tension Force Modeling）；

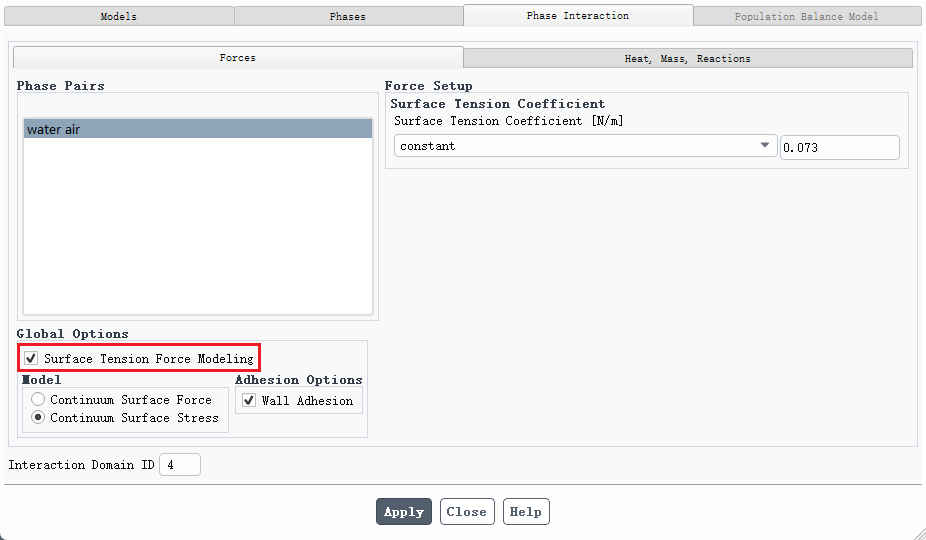
韦伯数越小表示表面张力越重要，比如毛细管现象、肥皂泡、液滴等小尺度问题。再比如雨滴下落时的形状就与表面张力相关，而瀑布倾泻而下的水则可以忽略表面张力的影响。

在三角形和四面体网格上对表面张力效应的计算，不如在四边形和六面体网格上那样精确。因此，表面张力效应最为关键的区域应当采用四边形或六面体进行网格划分。

• 对比连续面力（CSF）和连续面应力（CSS）
  与连续表面力（CSF）方法相比，连续表面应力（CSS）方法几乎没有额外的优势，尤其是在涉及表面张力变化的情况下。由于压力梯度和表面张力的不平衡，CSS方法和CSF方法都会在界面处产生parasitic currents。

在CSF方法中，表面张力以一种非守恒的方式表示如下：

\[F_{CSF} = \sigma k \Delta \alpha \tag{3} \]

式中\(k\)表示曲率，该式只适用于恒定的表面张力。
对于变化的表面张力，连续表面力（CSF）公式要求你基于表面张力梯度，在与界面相切的方向上对一个额外的项进行建模。
在连续表面应力（CSS）方法中，表面张力以一种守恒的方式表示如下：

\[F_{CSS}=\nabla\cdot\left[\sigma\left(|\nabla \alpha|I - \frac{\nabla \alpha\otimes\nabla \alpha}{|\nabla \alpha|}\right)\right] \tag{4} \]

式中，\(I\)=单位张量，\(\sigma\)=表面张力系数，\(\otimes\)=两个向量的张量积：原始法向量和变换后的法向量，\(\alpha\)=体积分数。

连续表面应力（CSS）方法无需对曲率进行任何显式计算。因此，在诸如尖角等分辨率不足的区域，它在物理表现上更为出色。由于其守恒公式，CSS方法在对变化的表面张力进行建模时不需要任何额外的项 。

如果液体与固体表面之间存在附着力，此时需要打开Adhesion Options选项，并且需要在物面边界处设置接触角。

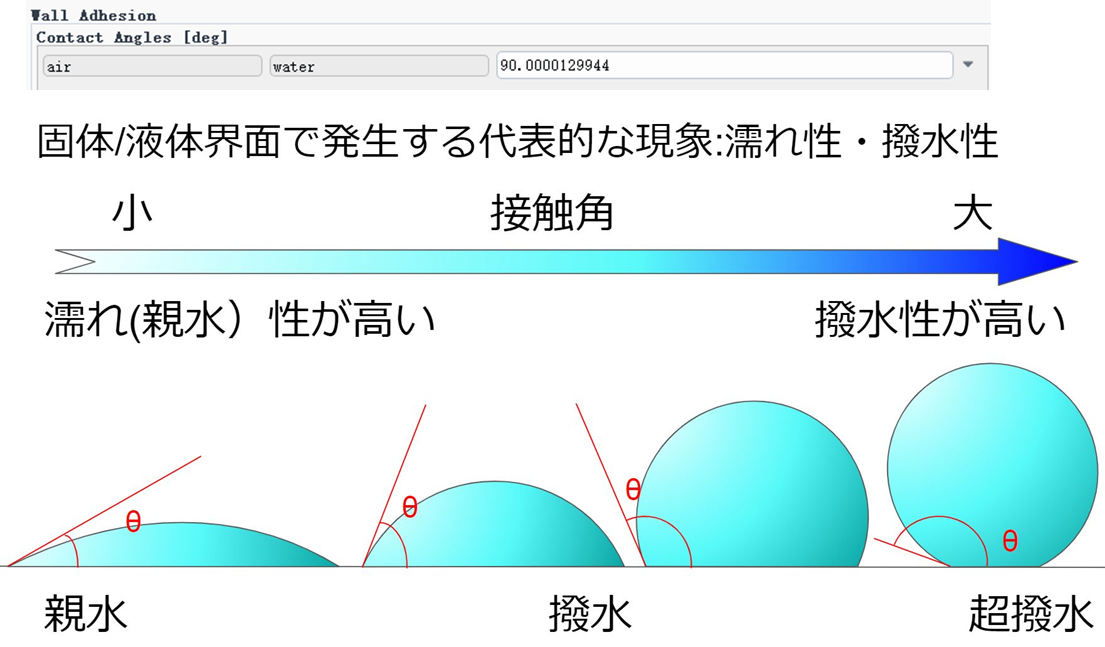
在考虑到表面张力时，推荐打开隐式体力（Implicit Body Force），这种处理方法通过考虑动量方程中压力梯度和表面张力的部分平衡，提高了求解的收敛性。