机器学习经典算法之PageRank
Google 的两位创始人都是斯坦福大学的博士生,他们提出的 PageRank 算法受到了论文影响力因子的评价启发。当一篇论文被引用的次数越多,证明这篇论文的影响力越大。正是这个想法解决了当时网页检索质量不高的问题。
/*请尊重作者劳动成果,转载请标明原文链接:*/
/* https://www.cnblogs.com/jpcflyer/p/11180263.html * /
一、 PageRank 的简化模型
我们先来看下 PageRank 是如何计算的。
我假设一共有 4 个网页 A、B、C、D。它们之间的链接信息如图所示:
这里有两个概念你需要了解一下。
出链指的是链接出去的链接。入链指的是链接进来的链接。比如图中 A 有 2 个入链,3 个出链。
简单来说,一个网页的影响力 = 所有入链集合的页面的加权影响力之和,用公式表示为:
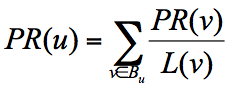
u 为待评估的页面, B_{u} 为页面 u 的入链集合。针对入链集合中的任意页面 v,它能给 u 带来的影响力是其自身的影响力 PR(v) 除以 v 页面的出链数量,即页面 v 把影响力 PR(v) 平均分配给了它的出链,这样统计所有能给 u 带来链接的页面 v,得到的总和就是网页 u 的影响力,即为 PR(u)。
所以你能看到,出链会给被链接的页面赋予影响力,当我们统计了一个网页链出去的数量,也就是统计了这个网页的跳转概率。
在这个例子中,你能看到 A 有三个出链分别链接到了 B、C、D 上。那么当用户访问 A 的时候,就有跳转到 B、C 或者 D 的可能性,跳转概率均为 1/3。
B 有两个出链,链接到了 A 和 D 上,跳转概率为 1/2。
这样,我们可以得到 A、B、C、D 这四个网页的转移矩阵 M:

我们假设 A、B、C、D 四个页面的初始影响力都是相同的,即:
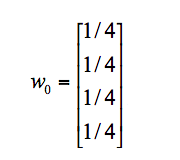
当进行第一次转移之后,各页面的影响力 w_{1} 变为:
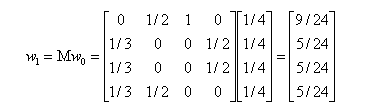
然后我们再用转移矩阵乘以 w_{1} 得到 w_{2} 结果,直到第 n 次迭代后 w_{n} 影响力不再发生变化,可以收敛到 (0.3333,0.2222,0.2222,0.2222),也就是对应着 A、B、C、D 四个页面最终平衡状态下的影响力。
你能看出 A 页面相比于其他页面来说权重更大,也就是 PR 值更高。而 B、C、D 页面的 PR 值相等。
至此,我们模拟了一个简化的 PageRank 的计算过程,实际情况会比这个复杂,可能会面临两个问题:
1. 等级泄露(Rank Leak):如果一个网页没有出链,就像是一个黑洞一样,吸收了其他网页的影响力而不释放,最终会导致其他网页的 PR 值为 0。
2. 等级沉没(Rank Sink):如果一个网页只有出链,没有入链(如下图所示),计算的过程迭代下来,会导致这个网页的 PR 值为 0(也就是不存在公式中的 V)。
针对等级泄露和等级沉没的情况,我们需要灵活处理。
比如针对等级泄露的情况,我们可以把没有出链的节点,先从图中去掉,等计算完所有节点的 PR 值之后,再加上该节点进行计算。不过这种方法会导致新的等级泄露的节点的产生,所以工作量还是很大的。
有没有一种方法,可以同时解决等级泄露和等级沉没这两个问题呢?
二、 PageRank 的随机浏览模型
为了解决简化模型中存在的等级泄露和等级沉没的问题,拉里·佩奇提出了 PageRank 的随机浏览模型。他假设了这样一个场景:用户并不都是按照跳转链接的方式来上网,还有一种可能是不论当前处于哪个页面,都有概率访问到其他任意的页面,比如说用户就是要直接输入网址访问其他页面,虽然这个概率比较小。
所以他定义了阻尼因子 d,这个因子代表了用户按照跳转链接来上网的概率,通常可以取一个固定值 0.85,而 1-d=0.15 则代表了用户不是通过跳转链接的方式来访问网页的,比如直接输入网址。
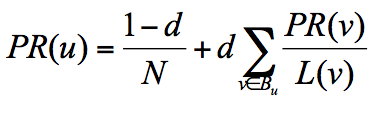
其中 N 为网页总数,这样我们又可以重新迭代网页的权重计算了,因为加入了阻尼因子 d,一定程度上解决了等级泄露和等级沉没的问题。
通过数学定理(这里不进行讲解)也可以证明,最终 PageRank 随机浏览模型是可以收敛的,也就是可以得到一个稳定正常的 PR 值。
三、 PageRank 在社交影响力评估中的应用
网页之间会形成一个网络,是我们的互联网,论文之间也存在着相互引用的关系,可以说我们所处的环境就是各种网络的集合。
只要是有网络的地方,就存在出链和入链,就会有 PR 权重的计算,也就可以运用我们今天讲的 PageRank 算法。
我们可以把 PageRank 算法延展到社交网络领域中。比如在微博上,如果我们想要计算某个人的影响力,该怎么做呢?
一个人的微博粉丝数并不一定等于他的实际影响力。如果按照 PageRank 算法,还需要看这些粉丝的质量如何。如果有很多明星或者大 V 关注,那么这个人的影响力一定很高。如果粉丝是通过购买僵尸粉得来的,那么即使粉丝数再多,影响力也不高。
同样,在工作场景中,比如说脉脉这个社交软件,它计算的就是个人在职场的影响力。如果你的工作关系是李开复、江南春这样的名人,那么你的职场影响力一定会很高。反之,如果你是个学生,在职场上被链入的关系比较少的话,职场影响力就会比较低。
同样,如果你想要看一个公司的经营能力,也可以看这家公司都和哪些公司有合作。如果它合作的都是世界 500 强企业,那么这个公司在行业内一定是领导者,如果这个公司的客户都是小客户,即使数量比较多,业内影响力也不一定大。
除非像淘宝一样,有海量的中小客户,最后大客户也会找上门来寻求合作。所以权重高的节点,往往会有一些权重同样很高的节点在进行合作。
四、 如何使用工具实现 PageRank 算法
PageRank 算法工具在 sklearn 中并不存在,我们需要找到新的工具包。实际上有一个关于图论和网络建模的工具叫 NetworkX,它是用 Python 语言开发的工具,内置了常用的图与网络分析算法,可以方便我们进行网络数据分析。
上节课,我举了一个网页权重的例子,假设一共有 4 个网页 A、B、C、D,它们之间的链接信息如图所示:
针对这个例子,我们看下用 NetworkX 如何计算 A、B、C、D 四个网页的 PR 值,具体代码如下:
1 import networkx as nx 2 3 # 创建有向图 4 5 G = nx.DiGraph() 6 7 # 有向图之间边的关系 8 9 edges = [("A", "B"), ("A", "C"), ("A", "D"), ("B", "A"), ("B", "D"), ("C", "A"), ("D", "B"), ("D", "C")] 10 11 for edge in edges: 12 13 G.add_edge(edge[0], edge[1]) 14 15 pagerank_list = nx.pagerank(G, alpha=1) 16 17 print("pagerank 值是:", pagerank_list)
NetworkX 工具把中间的计算细节都已经封装起来了,我们直接调用 PageRank 函数就可以得到结果:
1 pagerank 值是: {'A': 0.33333396911621094, 'B': 0.22222201029459634, 'C': 0.22222201029459634, 'D': 0.22222201029459634}
好了,运行完这个例子之后,我们来看下 NetworkX 工具都有哪些常用的操作。
1. 关于图的创建
图可以分为无向图和有向图,在 NetworkX 中分别采用不同的函数进行创建。无向图指的是不用节点之间的边的方向,使用 nx.Graph() 进行创建;有向图指的是节点之间的边是有方向的,使用 nx.DiGraph() 来创建。在上面这个例子中,存在 A→D 的边,但不存在 D→A 的边。
2.关于节点的增加、删除和查询
如果想在网络中增加节点,可以使用 G.add_node(‘A’) 添加一个节点,也可以使用 G.add_nodes_from([‘B’,‘C’,‘D’,‘E’]) 添加节点集合。如果想要删除节点,可以使用 G.remove_node(node) 删除一个指定的节点,也可以使用 G.remove_nodes_from([‘B’,‘C’,‘D’,‘E’]) 删除集合中的节点。
那么该如何查询节点呢?
如果你想要得到图中所有的节点,就可以使用 G.nodes(),也可以用 G.number_of_nodes() 得到图中节点的个数。
3. 关于边的增加、删除、查询
增加边与添加节点的方式相同,使用 G.add_edge(“A”, “B”) 添加指定的“从 A 到 B”的边,也可以使用 add_edges_from 函数从边集合中添加。我们也可以做一个加权图,也就是说边是带有权重的,使用 add_weighted_edges_from 函数从带有权重的边的集合中添加。在这个函数的参数中接收的是 1 个或多个三元组 [u,v,w] 作为参数,u、v、w 分别代表起点、终点和权重。
另外,我们可以使用 remove_edge 函数和 remove_edges_from 函数删除指定边和从边集合中删除。
另外可以使用 edges() 函数访问图中所有的边,使用 number_of_edges() 函数得到图中边的个数。
以上是关于图的基本操作,如果我们创建了一个图,并且对节点和边进行了设置,就可以找到其中有影响力的节点,原理就是通过 PageRank 算法,使用 nx.pagerank(G) 这个函数,函数中的参数 G 代表创建好的图。
五、 如何用 PageRank 揭秘希拉里邮件中的人物关系
了解了 NetworkX 工具的基础使用之后,我们来看一个实际的案例:希拉里邮件人物关系分析。
希拉里邮件事件相信你也有耳闻,对这个数据的背景我们就不做介绍了。你可以从 GitHub 上下载这个数据集: https://github.com/cystanford/PageRank
整个数据集由三个文件组成:Aliases.csv,Emails.csv 和 Persons.csv,其中 Emails 文件记录了所有公开邮件的内容,发送者和接收者的信息。Persons 这个文件统计了邮件中所有人物的姓名及对应的 ID。因为姓名存在别名的情况,为了将邮件中的人物进行统一,我们还需要用 Aliases 文件来查询别名和人物的对应关系。
整个数据集包括了 9306 封邮件和 513 个人名,数据集还是比较大的。不过这一次我们不需要对邮件的内容进行分析,只需要通过邮件中的发送者和接收者(对应 Emails.csv 文件中的 MetadataFrom 和 MetadataTo 字段)来绘制整个关系网络。因为涉及到的人物很多,因此我们需要通过 PageRank 算法计算每个人物在邮件关系网络中的权重,最后筛选出来最有价值的人物来进行关系网络图的绘制。
了解了数据集和项目背景之后,我们来设计到执行的流程步骤:
首先我们需要加载数据源;
在准备阶段:我们需要对数据进行探索,在数据清洗过程中,因为邮件中存在别名的情况,因此我们需要统一人物名称。另外邮件的正文并不在我们考虑的范围内,只统计邮件中的发送者和接收者,因此我们筛选 MetadataFrom 和 MetadataTo 这两个字段作为特征。同时,发送者和接收者可能存在多次邮件往来,需要设置权重来统计两人邮件往来的次数。次数越多代表这个边(从发送者到接收者的边)的权重越高;
在挖掘阶段:我们主要是对已经设置好的网络图进行 PR 值的计算,但邮件中的人物有 500 多人,有些人的权重可能不高,我们需要筛选 PR 值高的人物,绘制出他们之间的往来关系。在可视化的过程中,我们可以通过节点的 PR 值来绘制节点的大小,PR 值越大,节点的绘制尺寸越大。
设置好流程之后,实现的代码如下:
1 # -*- coding: utf-8 -*- 2 3 # 用 PageRank 挖掘希拉里邮件中的重要任务关系 4 5 import pandas as pd 6 7 import networkx as nx 8 9 import numpy as np 10 11 from collections import defaultdict 12 13 import matplotlib.pyplot as plt 14 15 # 数据加载 16 17 emails = pd.read_csv("./input/Emails.csv") 18 19 # 读取别名文件 20 21 file = pd.read_csv("./input/Aliases.csv") 22 23 aliases = {} 24 25 for index, row in file.iterrows(): 26 27 aliases[row['Alias']] = row['PersonId'] 28 29 # 读取人名文件 30 31 file = pd.read_csv("./input/Persons.csv") 32 33 persons = {} 34 35 for index, row in file.iterrows(): 36 37 persons[row['Id']] = row['Name'] 38 39 # 针对别名进行转换 40 41 def unify_name(name): 42 43 # 姓名统一小写 44 45 name = str(name).lower() 46 47 # 去掉, 和 @后面的内容 48 49 name = name.replace(",","").split("@")[0] 50 51 # 别名转换 52 53 if name in aliases.keys(): 54 55 return persons[aliases[name]] 56 57 return name 58 59 # 画网络图 60 61 def show_graph(graph, layout='spring_layout'): 62 63 # 使用 Spring Layout 布局,类似中心放射状 64 65 if layout == 'circular_layout': 66 67 positions=nx.circular_layout(graph) 68 69 else: 70 71 positions=nx.spring_layout(graph) 72 73 # 设置网络图中的节点大小,大小与 pagerank 值相关,因为 pagerank 值很小所以需要 *20000 74 75 nodesize = [x['pagerank']*20000 for v,x in graph.nodes(data=True)] 76 77 # 设置网络图中的边长度 78 79 edgesize = [np.sqrt(e[2]['weight']) for e in graph.edges(data=True)] 80 81 # 绘制节点 82 83 nx.draw_networkx_nodes(graph, positions, node_size=nodesize, alpha=0.4) 84 85 # 绘制边 86 87 nx.draw_networkx_edges(graph, positions, edge_size=edgesize, alpha=0.2) 88 89 # 绘制节点的 label 90 91 nx.draw_networkx_labels(graph, positions, font_size=10) 92 93 # 输出希拉里邮件中的所有人物关系图 94 95 plt.show() 96 97 # 将寄件人和收件人的姓名进行规范化 98 99 emails.MetadataFrom = emails.MetadataFrom.apply(unify_name) 100 101 emails.MetadataTo = emails.MetadataTo.apply(unify_name) 102 103 # 设置遍的权重等于发邮件的次数 104 105 edges_weights_temp = defaultdict(list) 106 107 for row in zip(emails.MetadataFrom, emails.MetadataTo, emails.RawText): 108 109 temp = (row[0], row[1]) 110 111 if temp not in edges_weights_temp: 112 113 edges_weights_temp[temp] = 1 114 115 else: 116 117 edges_weights_temp[temp] = edges_weights_temp[temp] + 1 118 119 # 转化格式 (from, to), weight => from, to, weight 120 121 edges_weights = [(key[0], key[1], val) for key, val in edges_weights_temp.items()] 122 123 # 创建一个有向图 124 125 graph = nx.DiGraph() 126 127 # 设置有向图中的路径及权重 (from, to, weight) 128 129 graph.add_weighted_edges_from(edges_weights) 130 131 # 计算每个节点(人)的 PR 值,并作为节点的 pagerank 属性 132 133 pagerank = nx.pagerank(graph) 134 135 # 将 pagerank 数值作为节点的属性 136 137 nx.set_node_attributes(graph, name = 'pagerank', values=pagerank) 138 139 # 画网络图 140 141 show_graph(graph) 142 143 144 145 # 将完整的图谱进行精简 146 147 # 设置 PR 值的阈值,筛选大于阈值的重要核心节点 148 149 pagerank_threshold = 0.005 150 151 # 复制一份计算好的网络图 152 153 small_graph = graph.copy() 154 155 # 剪掉 PR 值小于 pagerank_threshold 的节点 156 157 for n, p_rank in graph.nodes(data=True): 158 159 if p_rank['pagerank'] < pagerank_threshold: 160 161 small_graph.remove_node(n) 162 163 # 画网络图, 采用 circular_layout 布局让筛选出来的点组成一个圆 164 165 show_graph(small_graph, 'circular_layout')
运行结果如下:
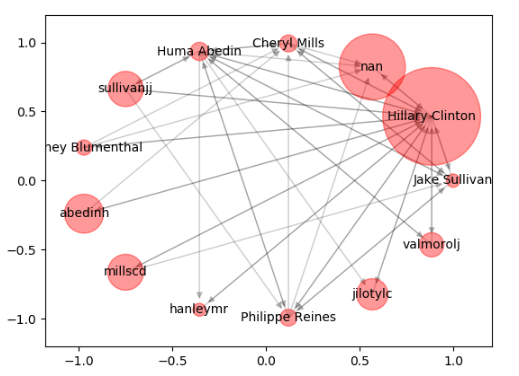
针对代码中的几个模块我做个简单的说明:
1. 函数定义
人物的名称需要统一,因此我设置了 unify_name 函数,同时设置了 show_graph 函数将网络图可视化。NetworkX 提供了多种可视化布局,这里我使用 spring_layout 布局,也就是呈中心放射状。
除了 spring_layout 外,NetworkX 还有另外三种可视化布局,circular_layout(在一个圆环上均匀分布节点),random_layout(随机分布节点 ),shell_layout(节点都在同心圆上)。
2. 计算边权重
邮件的发送者和接收者的邮件往来可能不止一次,我们需要用两者之间邮件往来的次数计算这两者之间边的权重,所以我用 edges_weights_temp 数组存储权重。而上面介绍过在 NetworkX 中添加权重边(即使用 add_weighted_edges_from 函数)的时候,接受的是 u、v、w 的三元数组,因此我们还需要对格式进行转换,具体转换方式见代码。
3.PR 值计算及筛选
我使用 nx.pagerank(graph) 计算了节点的 PR 值。由于节点数量很多,我们设置了 PR 值阈值,即 pagerank_threshold=0.005,然后遍历节点,删除小于 PR 值阈值的节点,形成新的图 small_graph,最后对 small_graph 进行可视化(对应运行结果的第二张图)。
搜索关注微信公众号“程序员姜小白”,获取更新精彩内容哦。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号