实验4

实验1

一元二次方程的根，不能设计成以函数返回值的方式返回给主调函数

实验2

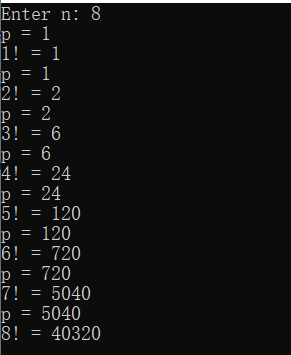
#include <stdio.h>
long long fac(int n);

int main() {
    int i,n;
    printf("Enter n: ");
    scanf("%d", &n);
    for(i=1; i<=n; ++i) 
        printf("%d! = %lld\n", i, fac(i)); 
    return 0;
}

long long fac(int n) {
    static long long p = 1;
    printf("p = %lld\n", p);
    p = p*n;
    return p;
}

#include<stdio.h>
int func(int, int);

int main() {
    int k=4,m=1,p1,p2;
    
    p1 = func(k,m) ; 
    p2 = func(k,m) ;
    printf("%d,%d\n",p1,p2) ;
    
    return 0;    
}

int func(int a,int b) {   
    static int m=0,i=2;
    
    i += m+1;
    m = i+a+b;  
    
    return (m);
}

局部static变量只赋初值一次，以后每次调用函数时不再重新赋初值而保留上次函数调用结束时的值。

实验3

#include <stdio.h>

#define N 1000
int fun(int n,int m,int bb[N]) {
    int i,j,k=0,flag;
    
    for(j=n;j<=m;j++) {
        flag=1;   
        for(i=2;i<j;i++)
            if(j%i==0) {  
               flag=0;
               break;
        }
        if(flag!=0) 
           bb[k++]=j;
    }
    return k;
}

int main(){
    int n=0,m=0,i,k,bb[N];
    
    scanf("%d",&n);
    scanf("%d",&m);
    
    for(i=0;i<m-n;i++)
        bb[i]=0;
        
    k=fun(n,m,bb); 
    
    for(i=0;i<k;i++)
        printf("%4d",bb[i]);
        
    return 0;
}

实验4

#include <stdio.h>
long long fun(int n);

int main() {
    int n;
    long long f;
    
    while(scanf("%d", &n) != EOF) {
        f = fun(n);
        printf("n = %d, f = %lld\n", n, f);
    }
    
    return 0;
}

long long fun(int n){
    long long k;
    if(n==0)
        k=0;
    if(n==1)
        k=1;
    if(n>=2)
        k=2*fun(n-1)+1;
    return k;
}

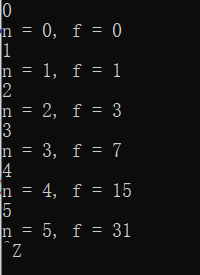
实验5

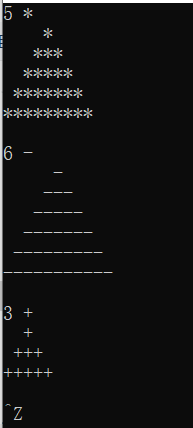
#include <stdio.h>

void draw(int n, char symbol);

#include <stdio.h> 
int main() {
    int n, symbol;
    
    while(scanf("%d %c", &n, &symbol) != EOF) {
        draw(n, symbol);
        
        printf("\n");
    }
    
    return 0;
} 

void draw(int n, char symbol){
    int x,y,z;
    for(x=1;x<=n;x++){
        for(y=1;y<=n-x;y++){
            printf(" ");
        }
        for(z=1;z<=2*x-1;z++){
            printf("%c",symbol);
        }printf("\n");
        }
    
}