线段树
线段树
基本的线段树就略过去了,基本线段树不会写这一年也白学了。
区间修改的时候要懒惰标记。如果有加和乘的话要考虑哪一个操作先。然后如果是乘的话一开始要初始化为 \(1\)
动态开点线段树:只有当访问到某个子节点的时候才开这个节点。
标记永久化:如果确定懒惰标记不会爆的话,可以不下传懒惰标记,而是在需要求的时候把那个值带在询问里面往下传。但是这个必须要求区间贡献独立。
还做了一道树链剖分的题目,那道题放到树链剖分里面去了。link,理论上来说树链剖分里面每一道题目都用了线段树。
T1 2824 排序
二分答案,将小于 \(mid\) 的值全部赋值为 \(1\) ,大于 \(mid\) 的值全部赋值为 \(0\),然后区间查询一下这里有多少个 \(1\)(或者反过来),这也就是当前的 \(mid\) 在哪一个位置,当这个位置是 \(q\) 的时候,那么就说明 \(mid\) 就是查询的值。(应该吧,郭总说这是整体二分模板题,找个时间把整体二分给学了)。
#define ir idx * 2 + 1
#define il idx * 2
#define L tr[idx].l
#define R tr[idx].r
struct node{
int l,r;
int sum,lazy;
}tr[N << 2];
struct wen{
lwl type;
lwl l,r;
}q[N];
int n,m,k,mid;
int w[N];
void push_up(int idx) {
tr[idx].sum = (tr[il].sum + tr[ir].sum);
}
void push_down(int idx) {
int t = tr[idx].lazy;
if (t == -1) return ;
int mid = (L + R) >> 1;
tr[il].sum = (mid - L + 1) * t;
tr[ir].sum = (R - mid) * t;
tr[il].lazy = tr[ir].lazy = t;
tr[idx].lazy = -1;
}
void build(int l,int r,int idx) {
if (l > r) return ;
L = l,R = r;
tr[idx].lazy = -1;
if (l == r) {
tr[idx].sum = (w[l] >= mid);
return ;
}
int mid = (L + R) >> 1;
if (mid >= l) build(l,mid,il);
if (mid < r) build(mid + 1,r,ir);
push_up(idx);
}
void update(int l,int r,int idx,int val) {
if (l > r) return ;
if (L >= l && R <= r) {
tr[idx].sum = (R - L + 1) * val;
tr[idx].lazy = val;
return ;
}
push_down(idx);
int mid = (L + R) >> 1;
if (mid >= l) update(l,r,il,val);
if (mid < r) update(l,r,ir,val);
push_up(idx);
}
int query(int l,int r,int idx) {
if (l > r) return 0;
if (L >= l && R <= r) {
return tr[idx].sum;
}
push_down(idx);
int ans = 0;
int mid = (L + R) >> 1;
if (mid >= l) ans += query(l,r,il);
if (mid < r) ans += query(l,r,ir);
return ans;
}
bool check() {
build(1,n,1);
for (int i = 1; i <= m; i ++) {
int type = q[i].type;
int l = q[i].l,r = q[i].r;
int cnt = query(l,r,1);
if (!type) {
update(r - cnt + 1,r,1,1);
update(l,r - cnt,1,0);
} else {
update(l,l + cnt - 1,1,1);
update(l + cnt,r,1,0);
}
}
return query(k,k,1);
}
int main(){
n = fr(),m = fr();
for (int i = 1; i <= n; i ++) w[i] = fr();
for (int i = 1; i <= m; i ++) {
q[i] = {fr(),fr(),fr()};
}
int l = 1,r = n;
int ans = 0;
k = fr();
while (l <= r) {
mid = (l + r) >> 1;
if (check()) ans = mid,l = mid + 1;
else r = mid - 1;
}
fw(ans);
return 0;
}
T2 3979 遥远的国度
如果不换根就是裸的树链剖分,于是单独考虑换根。
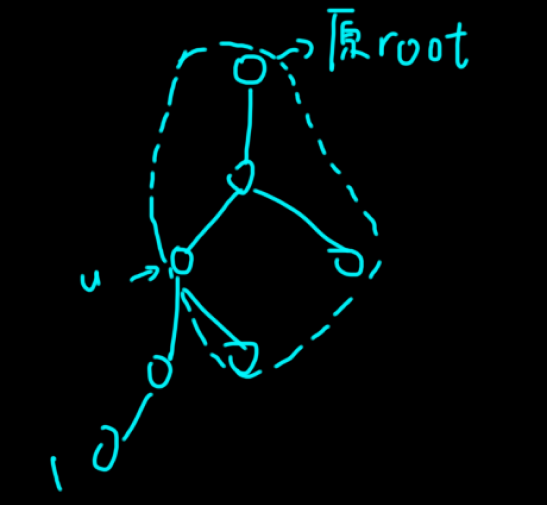
可以发现,换根其实只是对于子树的查询有影响,所以我们查询的时候我们就改一下查询方法,因为可以发现,如果将下图的 \(1\) 点改为根节点的话,那么 \(u\) 的子树就变成了框起来的那部分。可以发现,其实这个地方就是所有的点减去 \(u\) 所对应的二子节点的子树,那么我们就可以查询两个分开的区间,然后再在这两个区间里面取一个最小值。
T3 Legacy
线段树优化建图,建两颗线段树,第一棵线段树的边都是从上往下的,第二棵线段树的边都是从下往上的,然后边权都是 \(0\) (所以不能把他们建在一棵树上,要不然所有最短路都是 \(0\) 了)。建出来大概就是下面这个样子:
而对于每一个 \(2\) 操作,就从 \(tr2\) 的叶子节点向 \(tr1\) 的对应区间连边(也就是下面绿色的边),而对于 \(3\) 操作来说,我们就从 \(tr2\) 的根节点向 \(tr1\) 的叶子结点连边。
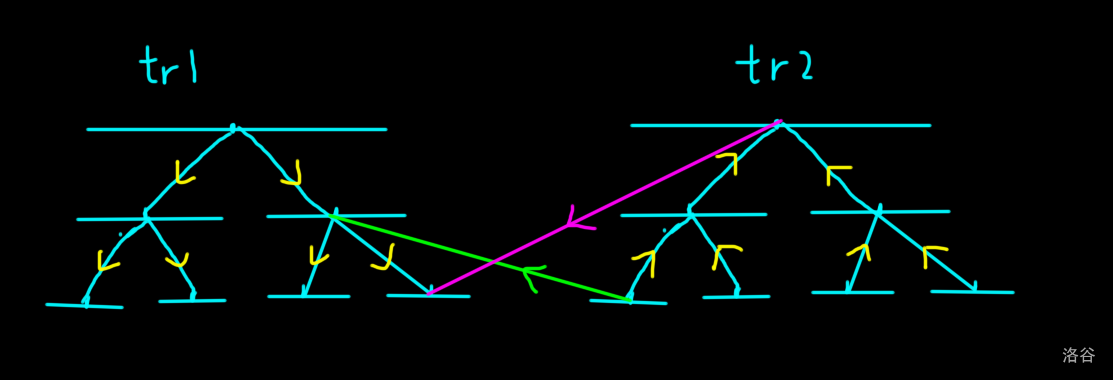
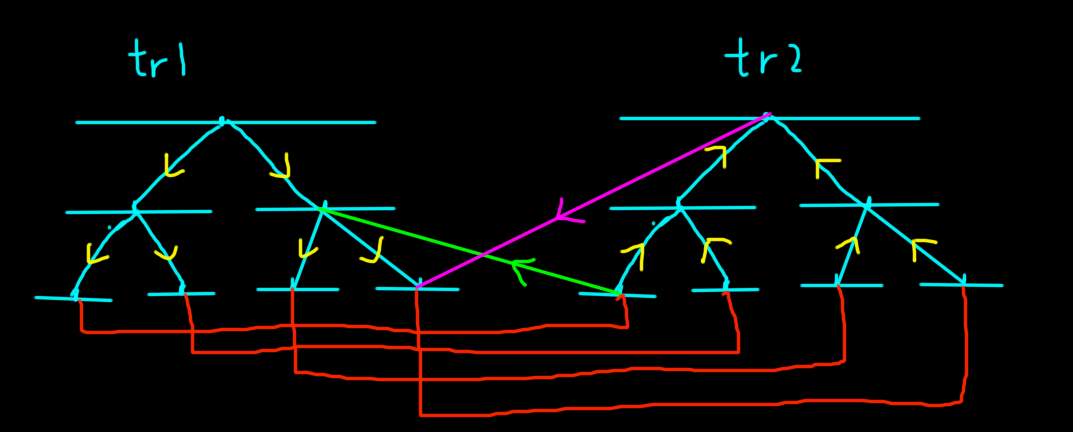
除此之外,还需要连的边是叶子结点和叶子结点之间的边,因为两棵不同的树的同一个叶子节点对应图中的点是一样的,所以说同样的叶子节点之间要连权值为 \(0\) 的边。(也就是下面的红边)
最后跑一遍最短路就可以了。
注意这一题要开 \(lwl\) ,不仅是 \(dis\) 数组,还有 \(dij\) 里面那个优先队列也要开 \(lwl\)
struct node{
int l,r;
}tr1[N << 2],tr2[N << 2];
struct Node{
int v,w;
};
int n,m,st,tot;
vector<Node> e[N << 3];
int leaf1[N],leaf2[N];
lwl dis[N << 4];
bool flag[N << 4];
void add(int a,int b,int val) {
e[a].push_back({b,val});
}
// up to down
void build_1(int l,int r,int idx) {
int &L = tr1[idx].l,&R = tr1[idx].r;
if (l > r) return ;
L = l,R = r;
if (l == r) {
leaf1[l] = idx;
return ;
}
int mid = (L + R) >> 1;
build_1(l,mid,il);
build_1(mid + 1,r,ir);
add(idx,il,0),add(idx,ir,0);
}
// down to up
void build_2(int l,int r,int idx) {
int &L = tr2[idx].l,&R = tr2[idx].r;
if (l > r) return ;
L = l,R = r;
if (l == r) {
leaf2[l] = idx + tot;
add(leaf1[l],leaf2[l],0);
add(leaf2[l],leaf1[l],0);
return ;
}
int mid = (L + R) >> 1;
build_2(l,mid,il);
build_2(mid + 1,r,ir);
add(il + tot,idx + tot,0),add(ir + tot,idx + tot,0);
}
void add_1(int l,int r,int idx,int from,int val) {
int &L = tr1[idx].l,&R = tr1[idx].r;
if (L >= l && R <= r) {
add(from,idx,val);
return ;
}
int mid = (L + R) >> 1;
if (mid >= l) add_1(l,r,il,from,val);
if (mid < r) add_1(l,r,ir,from,val);
}
void add_2(int l,int r,int idx,int to,int val) {
int &L = tr2[idx].l,&R = tr2[idx].r;
if (L >= l && R <= r) {
add(idx + tot,to,val);
return ;
}
int mid = (L + R) >> 1;
if (mid >= l) add_2(l,r,il,to,val);
if (mid < r) add_2(l,r,ir,to,val);
}
void dij() {
memset(dis,0x3f,sizeof dis);
priority_queue<pii,vector<pii>,greater<pii> > q;
dis[leaf2[st]] = 0;
q.push({dis[leaf2[st]],leaf2[st]});
while (q.size()) {
auto u = q.top().se;
q.pop();
if (flag[u]) continue;
for (auto it : e[u]) {
int v = it.v,w = it.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({dis[v],v});
}
}
flag[u] = true;
}
}
int main(){
n = fr(),m = fr(),st = fr();
build_1(1,n,1);
tot = n << 2;
build_2(1,n,1);
while (m --) {
int type = fr();
if (type == 1) {
int u = fr(),v = fr(),w = fr();
add(leaf2[u],leaf1[v],w);
} else if (type == 2) {
int u = fr(),l = fr(),r = fr(),w = fr();
add_1(l,r,1,leaf2[u],w);
} else {
int v = fr(),l = fr(),r = fr(),w = fr();
add_2(l,r,1,leaf1[v],w);
}
}
dij();
for (int i = 1; i <= n; i ++) {
if (dis[leaf1[i]] > linf / 2) fw(-1);
else fw(dis[leaf1[i]]);
kg;
}
return 0;
}
练习
今天的题做且仅会做第一题。你妈的。鉴定为 \(B,C\) 题都是不可做题。等老师的代码吧。
A.快递小哥
线段树优化建树,这个是区间和区间之间连边,和前面那个差不多。然后一开始有好多人因为没有输出 \(-1\) \(WA\) 了,但是我写了,乐。
区间连区间的话和前面那个差不多,但是多点连多点有点麻烦,所以为每一组边减一个虚点,最后距离除以 \(2\) 也可以(潇潇写的是连两个点然后这两个点之间的边有权值,然后两个区间连向这两个点,边权为 \(0\))
一开始这道题 \(dij\) 写错了,恼。
struct node{
int l,r;
};
struct Node{
int v,w;
};
int n,m,st;
int tot = 0;
node tr1[N << 2],tr2[N << 2];
vector<Node> e[N << 4];
int leaf1[N],leaf2[N];
int dis[N << 4],flag[N << 4];
void add(int a,int b,int val) {
e[a].push_back({b,val});
}
// from up -> down
void build_1(int l,int r,int idx) {
int &L = tr1[idx].l,&R = tr1[idx].r;
if (l > r) return ;
L = l,R = r;
if (l == r) {
leaf1[l] = idx;
return ;
}
int mid = (l + r) >> 1;
build_1(l,mid,il);
build_1(mid + 1,r,ir);
add(idx,il,0),add(idx,ir,0);
}
// from down -> up
void build_2(int l,int r,int idx) {
int &L = tr2[idx].l,&R = tr2[idx].r;
if (l > r) return ;
L = l,R = r;
if (l == r) {
leaf2[l] = idx + tot;
return ;
}
int mid = (l + r) >> 1;
build_2(l,mid,il);
build_2(mid + 1,r,ir);
add(il + tot,idx + tot,0),add(ir + tot,idx + tot,0);
}
void add_1(int l,int r,int idx,int to) {
int &L = tr1[idx].l,&R = tr1[idx].r;
if (L >= l && R <= r) {
add(to,idx,1);
return ;
}
int mid = (L + R) >> 1;
if (mid >= l) add_1(l,r,il,to);
if (mid < r) add_1(l,r,ir,to);
}
void add_2(int l,int r,int idx,int to) {
int &L = tr2[idx].l,&R = tr2[idx].r;
if (L >= l && R <= r) {
add(idx + tot,to,1);
return ;
}
int mid = (L + R) >> 1;
if (mid >= l) add_2(l,r,il,to);
if (mid < r) add_2(l,r,ir,to);
}
void dij() {
memset(flag,0,sizeof flag);
memset(dis,0x3f,sizeof dis);
priority_queue<pii,vector<pii>,greater<pii> > q;
dis[leaf2[st]] = 0;
q.push({dis[leaf2[st]],leaf2[st]});
while (q.size()) {
auto u = q.top().se;
q.pop();
if (flag[u]) continue;
for (auto it : e[u]) {
int v = it.v,w = it.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({dis[v],v});
}
}
flag[u] = true;
}
}
int main(){
n = fr(),m = fr(),st = fr();
build_1(1,n,1);
tot = n << 2;
build_2(1,n,1);
int k = n << 3;
for (int i = 1; i <= n; i ++) {
add(leaf1[i],leaf2[i],0);
add(leaf2[i],leaf1[i],0);
}
while (m --) {
int a = fr(),b = fr(),c = fr(),d = fr();
k ++;
add_1(a,b,1,k);
add_2(c,d,1,k);
k ++;
add_1(c,d,1,k);
add_2(a,b,1,k);
}
dij();
for (int i = 1; i <= n; i ++) {
if (dis[leaf1[i]] >= inf) wj;
else {
fw(dis[leaf1[i]] / 2);
ch;
}
}
return 0;
}
B.菜鸟驿站
对着代码意会一下吧()
#define L tr[idx].l
#define R tr[idx].r
#define ir idx * 2 + 1
#define il idx * 2
struct node{
int l,r;
int maxn,lazy;
}tr[N << 2];
int n[2];
char s[2][N];
int w[2][N],qwq[4][N << 2];
int tot[N],nw[N],lis[N << 2];
void push_up(int idx) {
tr[idx].maxn = max(tr[il].maxn,tr[ir].maxn);
}
void push_down(int idx) {
if (!tr[idx].lazy) return ;
int t = tr[idx].lazy;
tr[idx].lazy = 0;
tr[il].maxn += t,tr[ir].maxn += t;
tr[il].lazy += t,tr[ir].lazy += t;
}
void build(int l,int r,int idx) {
if (l > r) return ;
L = l,R = r;
tr[idx].lazy = 0;
if (l == r) {
tr[idx].maxn = lis[l];
return ;
}
int mid = (L + R) >> 1;
build(l,mid,il);
build(mid + 1,r,ir);
push_up(idx);
}
void update(int l,int r,int idx,int val) {
if (l > r) return ;
if (L >= l && R <= r) {
tr[idx].lazy += val;
tr[idx].maxn += val;
return ;
}
push_down(idx);
int mid = (L + R) >> 1;
if (mid >= l) update(l,r,il,val);
if (mid < r) update(l,r,ir,val);
push_up(idx);
}
int main(){
int T = fr();
while (T --) {
scanf("%s%s",s[0] + 1,s[1] + 1);
n[0] = strlen(s[0] + 1),n[1] = strlen(s[1] + 1);
memset(tot,0,sizeof tot);
memset(nw,0,sizeof nw);
for (int i = 0; i < 2; i ++) {
for (int j = 1; j <= n[i]; j ++) {
if (s[i][j] == 'A') w[i][j] = 1;
else if (s[i][j] == 'C') w[i][j] = 2;
else if (s[i][j] == 'G') w[i][j] = 3;
else w[i][j] = 0;
tot[w[i][j]] ++;
}
}
for (int i = 0; i < 4; i ++) {
for (int j = 1; j <= n[0] + n[1]; j ++) {
qwq[i][j] = inf;
}
}
memset(lis,0,sizeof lis);
for (int i = 1; i <= n[1] + 1; i ++) {
if (i != n[1] + 1) qwq[w[1][i]][++ nw[w[1][i]]] = i;
for (int j = 0; j < 4; j ++)
lis[i] += min(nw[j],tot[j] - nw[j]);
}
build(0,n[1],1);
memset(nw,0,sizeof nw);
int ans = tr[1].maxn;
for (int i = 1; i <= n[0]; i ++) {
int t = w[0][i];
++ nw[t];
if (nw[t] > (tot[t] + 1) / 2) {
update(0,n[1],1,-1);
} else {
update(0,min(qwq[t][tot[t] / 2 - nw[t] + 1],n[1]) - 1,1,1);
update(qwq[t][(tot[t] + 1) / 2 - nw[t] + 1],n[1],1,-1);
}
ans = max(ans,tr[1].maxn);
}
fw(ans);
ch;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号