树链剖分

前置

先来看两个问题：

将树从 \(x\) 节点到 \(y\) 节点最短路径上所有点的权值都加上 \(z\)

很容易想到，我们可以通过树上差分来解决这个问题

求树上从 \(x\) 节点到 \(y\) 节点最短路径上所有节点的值的和

这个也是很简单的，就是 \(LCA\) 就可以了，我们先 \(dfs\) 处理每个点到根节点的 \(dis\) ，然后再通过 \(LCA\) 求出两个节点的最近公共祖先就可以很容易的求出来了。

但是如果这两个问题结合起来，称为一道题的两种操作这两个方法显然就不适用了，那么就要用到树链剖分了。

简要

树链剖分是解决树上问题的一种常见的数据结构，对于树上路径修改以及路径信息查询等问题有着较优的复杂度

树链剖分分为两种：重链剖分 & 长链剖分。但是长链剖分不常见，应用也不广泛，所以通常说的树剖都是重链剖分。

一些重链剖分的专业名词

重儿子（重节点）：每个点的子树中，子树大小（即节点数最大的子节点）
轻儿子（轻节点）：除了重儿子以外的其他子节点
重边：每个节点与其重儿子之间的边
轻边：每个节点与其轻儿子之间的边
重链：多条重边连成的链
轻链：多条轻边连成的链

关于树剖，最基本的就是求取 \(LCA\) ，而他的时间复杂度到达了 \(O(\log n)\) ，虽然说比不上离线的 \(tarjan\) ，但是后者常数很大，因此树剖便成为了不二之选。

过程

首先，我们先假设一棵树是长这个样子的：

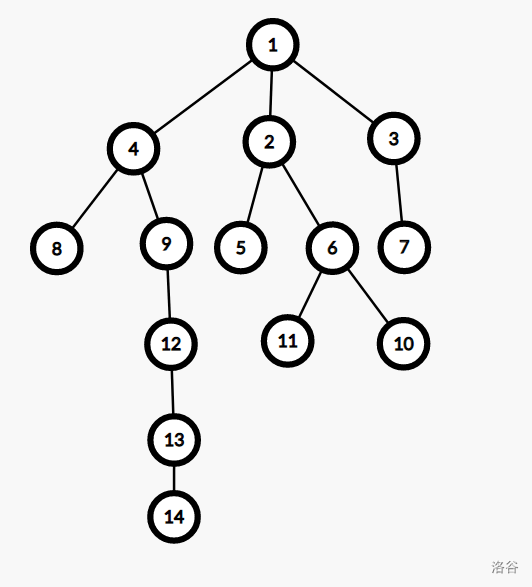
不难发现，这棵树的重链就是 \(1,4,9,12,13,14\) 。

树链剖分求 \(LCA\) 的的思想就是把一个图剖分成 \(\log n\) 条链，然后在链上进行跳跃。

首先我们先定义一下数组来存储上面提到的概念：

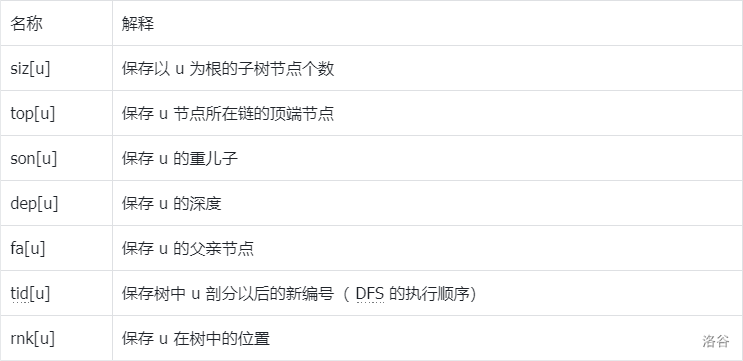
除此之外，还包含两个性质：

如果 \((u,v)\) 是一条轻边，那么 \(siz[u] < siz[v] / 2\)
从根节点到任意节点的路所经过的轻重链个数都必定小于 \(\log n\)

算法大致需要两次 \(DFS\) ，第一次 \(DFS\) 得到当前节点的父亲节点、当前节点的深度值、当前节点的子节点数量、当前节点的重节点

void dfs1(int u,int father) {
	de[u] = de[father] + 1;
	fa[u] = father;
	siz[u] = 1;
	
	for (auto it : e[u]) {
		int v = it.v;
		if (v == father) continue;
		dfs1(v,u);
		siz[u] += siz[v];
		if (son[u] == -1 || siz[v] > siz[son[u]]) son[u] = v;
	}
}

第二次 \(DFS\) 的时候则可以将各个重节点连接成重链，轻节点连接成轻链，并且将重链（其实就是一段区间）用数据结构（一般是线段树或者树状数组）来进行维护，并且为每个节点重新编号，其实也就是 \(DFS\) 在执行时的顺序，同时记录当前节点所在链的起点，还有当前节点在树中的位置。

void dfs2(int u,int st) {
	// 当前节点，起始的重节点
	cnt ++;
	top[u] = st;
	tid[u] = cnt;
	rnk[cnt] = u;
	
	// 如果 u 不在重链上，则不处理
	if (son[u] == -1) return ;
	
	dfs2(son[u],st);
	for (auto it : e[u]) {
		int v = it.v;
		if (v != son[u] && v != fa[u]) {
			//如果 v 不是 u 的重节点或者父亲，则将其的 top 设置为 v
			dfs2(v,v);
		}
	}
}

而修改和查询操作的原理是类似的，以查询操作位例，其实就是一个 \(LCA\) ，不过这里用了 \(top\) 来加速，因为 \(top\) 可以直接跳到该重链的起始节点，轻链没有起始节点之说，他们的 \(top\) 就是自己。需要注意的一点是，每次循环只能跳转一次，并且让节点深的那个来跳到 \(top\) 的位置，避免两个点一起跳从而擦肩而过。

这里面的 \(query\) 和 \(update\) 函数就是线段树或者树状数组的函数。

lwl query_path(int x,int y) {
	lwl ans = 0;
	// 直到两个节点所在链的起始点相等才找到了 LCA
	int hx = top[x],hy = top[y];
	while (hx != hy) {
		if (de[hx] < de[hy]) swap(x,y);
		ans += query(1,n,tid[top[x]],tid[x],1);
		ans %= mod;
		x = fa[x];
		hx = top[x],hy = top[y];
	}
	
	if (tid[x] > tid[y]) swap(x,y);
	ans += query(1,n,tid[x],tid[y],1);
	return ans % mod;
}

void update_path(int x,int y,lwl val) {
	int hx = top[x],hy = top[y];
	while (hx != hy) {
		if (de[hx] < de[hy]) swap(x,y);
		update(1,n,tid[top[x]],tid[x],1,val);
		x = fa[x];
		hx = top[x],hy = top[y];
	}
	
	if (tid[x] > tid[y]) swap(x,y);
	update(1,n,tid[x],tid[y],1,val);
}

应用

T1 模板 3384 重链剖分

调的人想死，谢谢 \(y\) 总的代码，不然我得调死。

点击查看代码

#include<bits/stdc++.h>
#define kg putchar(' ')
#define ch puts("")
#define wj puts("-1")
#define se second
#define fi first
#define ri register int
#define ir idx * 2 + 1
#define il idx * 2
#define hx top[x]
#define hy top[y]
using namespace std;
typedef long long lwl;

const int N = 2e5 + 5, inf = 0x3f3f3f3f;
const double dinf = 929 * 1e12;
const lwl linf = 0x3f3f3f3f3f3f3f3f;

struct node{
	lwl sum;
	lwl lazy;
}tr[N << 2];

lwl n,m,rt,cnt,mod;
lwl siz[N],fa[N],son[N],top[N],de[N];
lwl tid[N],rnk[N];
lwl w[N];
vector<int> e[N];

void dfs1(int u,int father) {
	de[u] = de[father] + 1;
	fa[u] = father;
	siz[u] = 1;
	
	for (auto it : e[u]) {
		int v = it;
		if (v == father) continue;
		dfs1(v,u);
		siz[u] += siz[v];
		if (siz[v] > siz[son[u]]) son[u] = v;
	}
}

void dfs2(int u,int st) {
	// 当前节点，起始的重节点
	cnt ++;
	top[u] = st;
	tid[u] = cnt;
	rnk[cnt] = u;
	
	// 如果 u 不在重链上，则不处理
	if (!son[u]) return ;
	
	dfs2(son[u],st);
	for (auto it : e[u]) {
		int v = it;
		if (v != son[u] && v != fa[u]) {
			//如果 v 不是 u 的重节点或者父亲，则将其的 top 设置为 v
			dfs2(v,v);
		}
	}
}

void push_up(int idx) {
	tr[idx].sum = (tr[ir].sum + tr[il].sum) % mod;
}

void push_down(int idx,int l,int r) {
	if (!tr[idx].lazy) return ;
	int t = tr[idx].lazy;
	int mid = (l + r) >> 1;
	tr[ir].sum = (tr[ir].sum + (r - mid) * t) % mod;
	tr[ir].lazy = (tr[ir].lazy + t) % mod;
	tr[il].sum = (tr[il].sum + (mid - l + 1) * t) % mod;
	tr[il].lazy = (tr[il].lazy + t) % mod;
	tr[idx].lazy = 0;
}

void build(int l,int r,int idx) {
	if (l == r) {
		tr[idx].sum = w[rnk[l]];
		tr[idx].lazy = 0;
		return ;
	}
	int mid = (l + r) >> 1;
	build(l,mid,il);
	build(mid + 1,r,ir);
	push_up(idx);
}

void update(int L,int R,int l,int r,int idx,lwl x) {
	if (L >= l && R <= r) {
		tr[idx].sum += (lwl)(R - L + 1) * x % mod;
		tr[idx].sum %= mod;
		tr[idx].lazy += x;
		tr[idx].lazy %= mod;
		return ;
	}
	push_down(idx,L,R);
	int mid = (L + R) >> 1;
	if (mid >= l) update(L,mid,l,r,il,x);
	if (mid < r) update(mid + 1,R,l,r,ir,x);
	push_up(idx);
}

lwl query(int L,int R,int l,int r,int idx) {
	if (L >= l && R <= r) {
		return tr[idx].sum;
	}
	push_down(idx,L,R);
	lwl ans = 0;
	int mid = (L + R) >> 1;
	if (mid >= l) ans += query(L,mid,l,r,il);
	if (mid < r) ans += query(mid + 1,R,l,r,ir);
	return ans % mod;
}

lwl query_path(int x,int y) {
	lwl ans = 0;
	// 直到两个节点所在链的起始点相等才找到了 LCA
	while (hx != hy) {
		if (de[hx] < de[hy]) swap(x,y);
		ans += query(1,n,tid[hx],tid[x],1);
		ans %= mod;
		x = fa[hx];
	}
	
	if (de[x] > de[y]) swap(x,y);
	ans += query(1,n,tid[x],tid[y],1);
	return ans % mod;
}

void update_path(int x,int y,lwl val) {
	while (hx != hy) {
		if (de[hx] < de[hy]) swap(x,y);
		update(1,n,tid[hx],tid[x],1,val);
		x = fa[hx];
	}
	
	if (tid[x] > tid[y]) swap(x,y);
	update(1,n,tid[x],tid[y],1,val);
}

signed main(){
	n = fr(),m = fr(),rt = fr(),mod = fr();
	for (int i = 1; i <= n; i ++) {
		w[i] = fr();
	}
	for (int i = 1 ; i < n; i ++) {
		int a = fr(),b = fr();
		e[a].push_back(b);
		e[b].push_back(a);
	}
	cnt = 0;
	dfs1(rt,0);
	dfs2(rt,0);
	build(1,n,1);
	for (int i = 1; i <= m; i ++) {
		int type = fr();
		if (type == 1) {
			int x = fr(),y = fr(),k = fr();
			update_path(x,y,k);
		} else if (type == 2) {
			int x = fr(),y = fr();
			lwl ans = query_path(x,y);
			fw(ans),ch;
		} else if (type == 3) {
			int x = fr(),y = fr();
			update(1,n,tid[x],tid[x] + siz[x] - 1,1,y);
		} else {
			int x = fr();
			lwl ans = query(1,n,tid[x],tid[x] + siz[x] - 1,1);
			fw(ans % mod),ch;
		}
	}
	return 0;
}

T2 Tourist

树链剖分+圆方树+线段树（也算是包含在树链剖分里面的吧（？））

圆方树的话看强连通那个博客link

感觉还是比较裸的题目，就是用的东西有点多。

点击查看代码

#define hx top[x]
#define hy top[y]

int n,m,Q,cnt,tot;
int w[N],h[N];
int dfn[N],low[N],timestamp;
int tid[N],top[N],siz[N],fa[N],son[N],rnk[N],de[N];
multiset<int> s[N];
int tr[N << 2];
stack<int> stk;
vector<int> e[N],edge[N];

void tarjan(int u) {
	dfn[u] = low[u] = ++timestamp;
	stk.push(u);
	for (auto v : edge[u]) {
		if (!dfn[v]) {
			tarjan(v);
			low[u] = min(low[v],low[u]);
			if (low[v] >= dfn[u]) {
				tot ++;
				while (stk.size()) {
					auto t = stk.top();
					stk.pop();
					e[tot].push_back(t);
					e[t].push_back(tot);
					h[t] = tot;
					if (t == v) break;
				}
				e[tot].push_back(u);
				e[u].push_back(tot);
			}
		} else low[u] = min(low[u],dfn[v]);
	}
}

void dfs1(int u,int father) {
	fa[u] = father;
	de[u] = de[father] + 1;
	siz[u] = 1;
	
	for (auto v : e[u]) {
		if (v == father) continue;
		dfs1(v,u);
		siz[u] += siz[v];
		if (siz[v] > siz[son[u]]) son[u] = v;
	}
}

void dfs2(int u,int st) {
	cnt ++;
	top[u] = st;
	tid[u] = cnt;
	rnk[cnt] = u;
	
	if (!son[u]) return ;
	dfs2(son[u],st);
	
	for (auto v : e[u]) {
		if (v == fa[u]) continue;
		if (v == son[u]) continue;
		dfs2(v,v);
	}
}

void push_up(int idx) {
	tr[idx] = min(tr[il],tr[ir]);
}

void build(int l,int r,int idx) {
	if (l > r) return ;
	if (l == r) {
		tr[idx] = w[rnk[l]];
		return ;
	}
	int mid = (l + r) >> 1;
	build(l,mid,il);
	build(mid + 1,r,ir);
	push_up(idx);
}

void modify(int L,int R,int l,int r,int idx,int x) {
	if (L >= l && R <= r) {
		tr[idx] = x;
		return ;
	}
	int mid = (L + R) >> 1;
	if (mid >= l) modify(L,mid,l,r,il,x);
	if (mid < r) modify(mid + 1,R,l,r,ir,x);
	push_up(idx);
}

int query(int L,int R,int l,int r,int idx) {
	if (L >= l && R <= r) {
		return tr[idx];
	}
	int mid = (L + R) >> 1;
	int ans = inf;
	if (mid >= l) ans = min(ans,query(L,mid,l,r,il));
	if (mid < r) ans = min(ans,query(mid + 1,R,l,r,ir));
	return ans;
}

int query_path(int x,int y) {
	int ans = inf;
	
	while (hx != hy) {
		if (de[hx] < de[hy]) swap(x,y);
		ans = min(ans,query(1,tot,tid[hx],tid[x],1));
		x = fa[hx];
	}
	
	if (de[x] > de[y]) swap(x,y);
	ans = min(ans,query(1,tot,tid[x],tid[y],1));
	if (x > n) ans = min(ans,w[fa[x]]);
	return ans;
}

int main(){
	n = fr(),m = fr(),Q = fr();
	for (int i = 1; i <= n; i ++) {
		w[i] = fr();
	}
	for (int i = 1; i <= m; i ++) {
		int a = fr(),b = fr();
		edge[a].push_back(b);
		edge[b].push_back(a);
	}
	tot = n;
	for (int i = 1; i <= n; i ++) {
		if (!dfn[i]) tarjan(i);
	}
	dfs1(1,0);
	dfs2(1,1);
	for (int i = 2; i <= n; i ++) {
		s[fa[i]].insert(w[i]);
	}
	for (int i = n + 1; i <= tot; i ++) {
		if (s[i].empty()) w[i] = inf;
		else w[i] = *s[i].begin();
	}
	build(1,tot,1);
	while (Q --) {
		char type = getchar();
		while (type != 'A' && type != 'C')
			type = getchar();
		int a = fr(),b = fr();
		if (type == 'A') {
			int ans = query_path(a,b);
			fw(ans);
			ch;
		} else {
			modify(1,tot,tid[a],tid[a],1,b);
			if (a == 1) {
				w[a] = b;
				continue;
			}
			int p = fa[a];
			s[p].erase(s[p].find(w[a]));
			s[p].insert(b);
			int minn = *s[p].begin();
			if (minn == w[p]) {
				w[a] = b;
				continue;
			}
			modify(1,tot,tid[p],tid[p],1,minn);
			w[p] = minn,w[a] = b;
		}
	}
	return 0;
}

T3 2146 软件包管理器

这个安装就是把当前点到 \(1\) 点的路径上面的点的权值全部都改为 \(1\)，卸载就是把当前点的所有子树的权值都改为 \(0\)，求答案的时候就是 \(tr[1].sum\) 的绝对值的差。

改了一种线段树的写法，因为今天听说了动态开点，感觉这个比较好写动态开点，以后就这么写了（虽然应该不会用动态开点）。

点击查看代码

#define hx top[x]
#define hy top[y]
#define il idx * 2
#define ir idx * 2 + 1
#define L tr[idx].l
#define R tr[idx].r

struct node{
	int l,r;
	int sum;
	int lazy;
}tr[N << 2];

int n,m;
vector<int> e[N];
int siz[N],de[N],fa[N],son[N],tid[N],rnk[N],top[N];
int cnt;

void dfs1(int u,int father) {
	fa[u] = father;
	siz[u] = 1;
	de[u] = de[father] + 1;
	
	for (auto v : e[u]) {
		if (v == father) continue;
		dfs1(v,u);
		siz[u] += siz[v];
		if (siz[v] > siz[son[u]]) son[u] = v;
	}
}

void dfs2(int u,int st) {
	top[u] = st;
	cnt ++;
	tid[u] = cnt;
	rnk[cnt] = u;
	
	if (!son[u]) return ;
	dfs2(son[u],st);
	for (auto v : e[u]) {
		if (v == fa[u] || v == son[u]) continue;
		dfs2(v,v);
	}
}

void push_up(int idx) {
	tr[idx].sum = tr[il].sum + tr[ir].sum;
}

void push_down(int idx) {
	int mid = (L + R) >> 1;
	int t = tr[idx].lazy;
	if (t == -1) return ;
	tr[il].sum = t * (mid - L + 1);
	tr[ir].sum = t * (R - mid);
	tr[il].lazy = tr[ir].lazy = t;
	tr[idx].lazy = -1;
}

void build(int l,int r,int idx) {
	if (l > r) return ;
	L = l,R = r;
	tr[idx].lazy = -1;
	tr[idx].sum = 0;
	if (l == r) {
		return ;
	}
	int mid = (L + R) >> 1;
	build(l,mid,il);
	build(mid + 1,r,ir);
}

void update(int l,int r,int idx,int val) {
	if (L >= l && R <= r) {
		tr[idx].sum = val * (R - L + 1);
		tr[idx].lazy = val;
		return ;
	}
	push_down(idx);
	int mid = (L + R) >> 1;
	if (mid >= l) update(l,r,il,val);
	if (mid < r) update(l,r,ir,val);
	push_up(idx);
}

void update_path(int x,int y,int val) {
	while (hx != hy) {
		if (de[x] < de[y]) swap(x,y);
		update(tid[hx],tid[x],1,val);
		x = fa[hx];
	}
	
	if (de[x] < de[y]) swap(x,y);
	update(tid[y],tid[x],1,val);
}

int main(){
	n = fr();
	for (int i = 2; i <= n; i ++) {
		m = fr() + 1;
		e[m].push_back(i);
	}
	dfs1(1,0);
	dfs2(1,1);
	build(1,n,1);
	m = fr();
	string type;
	int x;
	int la = 0;
	while (m --) {
		cin >> type;
		x = fr() + 1;
		la = tr[1].sum;
		if (type == "install") {
			update_path(x,1,1);
		} else {
			update(tid[x],tid[x] + siz[x] - 1,1,0);
		}
		fw(abs(tr[1].sum - la));
		ch;
	}
	return 0;
}

posted @ 2023-07-21 20:16 jingyu0929 阅读(32) 评论(0) 收藏举报

刷新页面返回顶部

jingyu0929

树链剖分

树链剖分

前置

简要

过程

应用

T1 模板 3384 重链剖分

T2 Tourist

T3 2146 软件包管理器

公告