连通性有关问题
强连通
在有向图中,如果两个顶点 \(u,v\) 间有一条从 \(u\) 到 \(v\) 的路径,也有一条从 \(v\) 到 \(u\) 的路径,则称这两个点强连通
如果有向图中任意两个顶点都是强连通的,那么这张图就是强连通图。
性质:一个有向图 \(G\) 是强连通的,当且仅当 \(G\) 中有一个回路,他至少包含所有节点一次。
求法:\(tarjan\) 和 \(Kosaraju\) (不怎么用,一般都是用 \(tarjan\) )
割点和割边
在一个无向连通图中,如果删除其中一条边或者一个点之后,连通块的数量会变多,那么这个点或边事割点或割边。
一个顶点是割点,当且仅当:
-
\(u\) 为树根,且 \(u\) 有多余一个子树
-
非根节点 \(u\) ,后代 \(v\) 都不可以通过回退边回到 \(u\) 的祖先 \(w\)
割边:圈上的点一定不是割边
双连通分量
分为点双连通分量和边双连通分量两种,就是图中不存在割点就是点双,0不存在桥(割边)就是边双。
3387 模板 缩点
主要是记记 \(tarjan\) 的写法,真是好久没写了,上次写好像还是补 \(2022NOIP\) 的时候写的
int n,m,cnt;
vector<int> e[N];
vector<int> edge[N];
int dfn[N],low[N],timestamp;
bool flag[N];
int h[N],sum[N],ans[N];
int d[N],w[N];
stack<int> s;
void tarjan(int u) {
dfn[u] = low[u] = ++ timestamp;
s.push(u);
flag[u] = true;
for (auto v : e[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u],low[v]);
} else if (flag[v]) {
low[u] = min(low[u],dfn[v]);
}
}
if (dfn[u] == low[u]) {
cnt ++;
while (s.size()) {
auto t = s.top();
s.pop();
flag[t] = false;
h[t] = cnt;
sum[cnt] += w[t];
if (t == u) break;
}
}
}
void topsort() {
queue<int> q;
for (int i = 1; i <= cnt; i ++) {
if (!d[i]) {
q.push(i);
ans[i] += sum[i];
}
}
while (q.size()) {
auto u = q.front();
q.pop();
for (auto v : edge[u]) {
ans[v] = max(ans[v],ans[u] + sum[v]);
d[v] --;
if (!d[v]) q.push(v);
}
}
}
int main(){
n = fr(),m = fr();
for (int i = 1; i <= n; i ++)
w[i] = fr();
while (m --) {
int a = fr(),b = fr();
e[a].push_back(b);
}
for (int i = 1; i <= n; i ++) {
if (!dfn[i]) tarjan(i);
}
for (int i = 1; i <= n; i ++) {
int u = h[i];
for (auto v : e[i]) {
if (h[v] == u) continue;
edge[u].push_back(h[v]);
d[h[v]] ++;
}
}
topsort();
int res = 0;
for (int i = 1; i <= cnt; i ++)
res = max(res,ans[i]);
fw(res);
return 0;
}
2-SAT 问题
这种题目一般是给你很多个条件,然后每一个条件都类似于 \((a,b)\) 之间至少有一个条件成立。
然后这种情况下,我们就将每个要求都拆成两个点:\(a\) 和 \(\lnot a\) ,然后在对于每一个条件的处理的时候,我们就连两条边就可以了。
假设一个要求是 \((a \lor b)\) ,那我们就将其转化为 $ \lnot a \rightarrow b \land \lnot b \rightarrow a $
这个意思就是如果 \(\lnot a\) 的话那么 \(b\) 就成立,也就是说这个有向边代表的就是如果起点成立那么可以退出终点。
所以我们就可以推出这样一个表:
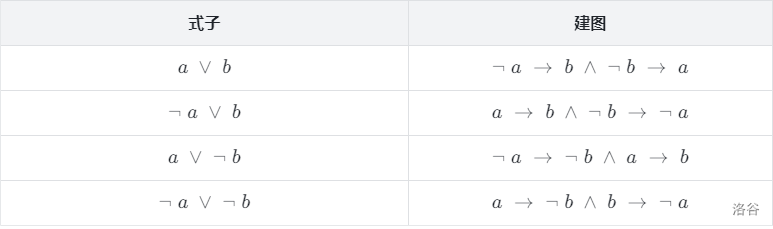
我们可以发现,将这个图建成之后,如果 \(a\) 和 \(\lnot a\) 在同一个连通块当中,那么这个问题就是无解的。
模板题 4782 2-SAT 问题
int n,m,cnt;
vector<int> e[N];
int dfn[N],low[N],timestamp;
bool flag[N];
int h[N],siz[N];
stack<int> s;
void tarjan(int u) {
dfn[u] = low[u] = ++ timestamp;
s.push(u);
flag[u] = true;
for (auto v : e[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u],low[v]);
} else if (flag[v]) low[u] = min(low[u],dfn[v]);
}
if (dfn[u] == low[u]) {
cnt ++;
while (s.size()) {
auto t = s.top();
s.pop();
flag[t] = false;
h[t] = cnt;
siz[cnt] ++;
if (t == u) break;
}
}
}
int main(){
n = fr(),m = fr();
while (m --) {
int i = fr(),a = fr();
int j = fr(),b = fr();
e[j + (1 - b) * n].push_back(i + a * n);
e[i + (1 - a) * n].push_back(j + b * n);
}
for (int i = 1; i <= 2 * n; i ++) {
if (!dfn[i]) tarjan(i);
}
for (int i = 1; i <= n; i ++) {
if (h[i] == h[i + n]) {
wj;
return 0;
}
}
yj;
for (int i = 1; i <= n; i ++) {
if (h[i] < h[i + n]) fw(0);
else fw(1);
kg;
}
return 0;
}
T1 4171 满汉全席
这个题目就是比较裸的模板题,和上面那个做法几乎一模一样,就是那个读数字的时候有的数字式两位或者更多的,所以要全部读进去而不能只考虑一位。
别问我是怎么知道的。
int n,m,cnt;
vector<int> e[N];
int dfn[N],low[N],timestamp;
bool flag[N];
int h[N];
stack<int> s;
void tarjan(int u) {
dfn[u] = low[u] = ++ timestamp;
s.push(u);
flag[u] = true;
for (auto v : e[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[v],low[u]);
} else if (flag[v]) low[u] = min(low[u],dfn[v]);
}
if (dfn[u] == low[u]) {
++ cnt;
while (s.size()) {
auto t = s.top();
s.pop();
flag[t] = false;
h[t] = cnt;
if (t == u) break;
}
}
}
int main(){
//freopen("qwq.in","r",stdin);
int T = fr();
while (T --) {
memset(dfn,0,sizeof dfn);
memset(low,0,sizeof low);
timestamp = 0,cnt = 0;
n = fr(),m = fr();
for (int i = 1; i <= n * 2; i ++) {
e[i].clear();
}
string s;
while (m --) {
cin >> s;
int i = 0,j = 0,a,b;
if (s[0] == 'm') a = 0;
else a = 1;
for (int h = 1; h < s.size(); h ++) {
i = i * 10 + s[h] - '0';
}
cin >> s;
if (s[0] == 'm') b = 0;
else b = 1;
for (int h = 1; h < s.size(); h ++) {
j = j * 10 + s[h] - '0';
}
e[i + (1 - a) * n].push_back(j + b * n);
e[j + (1 - b) * n].push_back(i + a * n);
}
for (int i = 1; i <= 2 * n; i ++) {
if (!dfn[i]) tarjan(i);
}
bool flag = true;
for (int i = 1; i <= n; i ++) {
if (h[i] == h[i + n]) {
flag = false;
wj;
break;
}
}
if (flag) yj;
}
return 0;
}
T2 3825 游戏
这个题感觉有点点暴力的样子,把所有 \(x\) 的情况都试一遍,然后每一种情况都跑一遍 \(tarjan\) 来判断这种情况有没有可能成立,如果成立的话就可以返回然后输出。
int n,m,cnt,d;
vector<int> e[N];
int dfn[N],low[N],timestamp;
bool flag[N];
stack<int> s;
char S[N];
int h[N],where[N];
int w[N][2];
char che[N][2];
bool st = false;
void tarjan(int u) {
dfn[u] = low[u] = ++ timestamp;
s.push(u);
flag[u] = true;
for (auto v : e[u]) {
if (! dfn[v]) {
tarjan(v);
low[u] = min(low[u],low[v]);
} else if (flag[v]) low[u] = min(low[u],dfn[v]);
}
if (dfn[u] == low[u]) {
cnt ++;
while (s.size()) {
auto t = s.top();
s.pop();
flag[t] = false;
h[t] = cnt;
if (t == u) break;
}
}
}
void init() {
cnt = 0,timestamp = 0;
memset(dfn,0,sizeof dfn);
memset(low,0,sizeof low);
memset(h,0,sizeof h);
for (int i = 1; i <= n * 3; i ++) {
e[i].clear();
}
}
int get(int i,char a) {
if (S[i] == 'a') {
if (a == 'B') return i;
else return i + n;
}
if (a == 'A') return i;
return i + n;
}
int f(int x) { // 取反
if (x > n) return x - n;
return x + n;
}
bool solve() {
init();
for (int k = 1; k <= m; k ++) {
int i = w[k][0];
char a = che[k][0];
int j = w[k][1];
char b = che[k][1];
if (S[i] == a + 'a' - 'A') continue;
if (S[j] == b + 'a' - 'A') {
i = get(i,a),j = get(j,b);
e[i].push_back(f(i));
continue;
}
i = get(i,a),j = get(j,b);
e[i].push_back(j);
e[f(j)].push_back(f(i));
}
for (int i = 1; i <= n * 2; i ++) {
if (!dfn[i]) tarjan(i);
}
for (int i = 1; i <= n; i ++) {
if (h[i] == h[i + n]) return false;
}
return true;
}
bool dfs(int u) {
if (u > d) {
if (solve()) return true;
return false;
}
for (int i = 0; i < 2; i ++) {
S[where[u]] = i + 'a';
if (dfs(u + 1)) return true;
}
return false;
}
int main(){
//freopen("qwq.in","r",stdin);
n = fr(),m = fr();
for (int i = 1; i <= n; i ++) {
S[i] = getchar();
if (S[i] == 'x') where[++ d] = i;
}
m = fr();
for (int i = 1; i <= m; i ++) {
w[i][0] = fr();
che[i][0] = getchar();
w[i][1] = fr();
che[i][1] = getchar();
}
if (!dfs(1)) {
wj;
return 0;
}
for (int i = 1; i <= n; i ++) {
if (S[i] == 'a') {
if (h[i] < h[i + n]) cout << "B";
else cout << "C";
} else if (S[i] == 'b') {
if (h[i] < h[i + n]) cout << "A";
else cout << "C";
} else {
if (h[i] < h[i + n]) cout << "A";
else cout << "B";
}
}
return 0;
}
圆方树
前置芝士:割点,点双连通分量
圆方树是一种无向图的重构树,通过对原图建立圆方树可以将原图上的某些问题转化到树上处理。
狭义圆方树
主要是说在仙人掌图中的应用(其他的我也不会,只写过一个仙人掌的)
仙人掌图:如果某个无向连通图的任意一条边最多只出现在一条简单回路里面的图。(简单回路就是在图上不重复经过任何一个顶点的回路)就像是下图(也就是不存在边同事属于多个环的无向连通图)
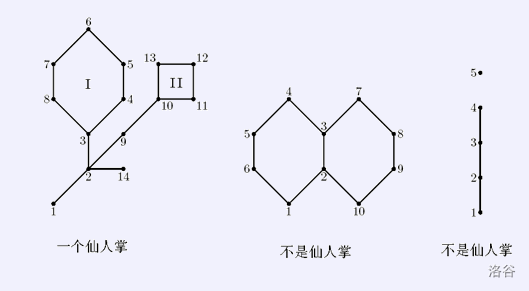
然后仙人掌的圆方树上面的圆点就是原图上的点,方点是我们构造出来对应一个环的点
在仙人掌图上构造圆方树的方法
-
如果一条边在仙人掌中不属于任何一个环,那么就直接将两个圆点连一条边。
-
对于每一个点双连通分量(也就是原图中的环)而言,我们都构造出一个方点,将环上的每一个点都向方点连一条边。这样构造的话我们就可以让一个方点对应一个环
eg:
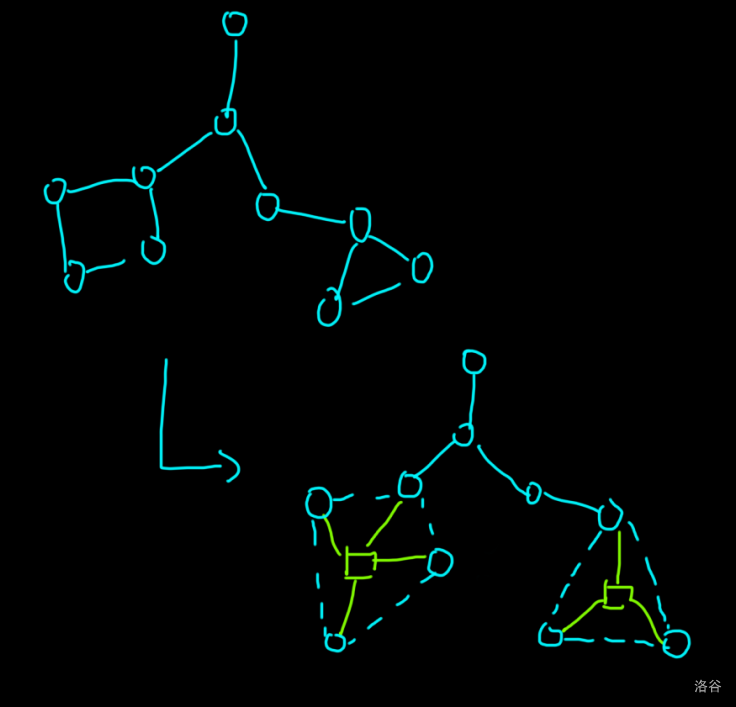
显而易见的是,这样建出来的新图就肯定是一个树,然后就可以用一些树的性质了。
然后这样建了圆方树之后原图的连通性什么的都是不会改变的,这个就用 \(tarjan\) 做就好了。
5236 静态仙人掌
struct node{
int v,w;
};
int cnt = 0;
int n,m,Q,nn;
int h[N],e[M],val[M],ne[M],idx;//原图
vector<node> edge[N]; //圆方树
int dfn[N],low[N],timestamp;
int s[N],stot[N],fu[N],hw[N],fe[N];
// 环的当前大小,环的总和,环的上一个点,每个点到头的最短距离
int fa[N][14],de[N],dis[N];//LCA
int X,Y;
void add(int a,int b,int w) {
e[idx] = b;
val[idx] = w;
ne[idx] = h[a];
h[a] = idx ++;
}
void build_circle(int x,int y,int z) {
int sum = z;
for (int k = y; k != x; k = fu[k]) {
s[k] = sum;
sum += hw[k];
}
s[x] = stot[x] = sum;
//建方点
edge[x].push_back({++nn,0});
for (int k = y; k != x; k = fu[k]) {
stot[k] = sum;
edge[nn].push_back({k,min(s[k],sum - s[k])});
}
}
void tarjan(int u,int from) {
dfn[u] = low[u] = ++ timestamp;
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i],w = val[i];
if (!dfn[v]) {
fu[v] = u,hw[v] = w,fe[v] = i;
tarjan(v,i);
low[u] = min(low[v],low[u]);
if (dfn[u] < low[v]) {
edge[u].push_back({v,w});
}
} else if (i != (from ^ 1)) {
low[u] = min(low[u],dfn[v]);
}
}
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (dfn[u] < dfn[v] && fe[v] != i) {
build_circle(u,v,val[i]);
}
}
}
void dfs(int u,int father) {
de[u] = de[father] + 1;
fa[u][0] = father;
for (int k = 1; k < 14; k ++)
fa[u][k] = fa[fa[u][k - 1]][k - 1];
for (auto it : edge[u]) {
int v = it.v;
dis[v] = dis[u] + it.w;
dfs(v,u);
}
}
int LCA(int x,int y) {
if (de[x] < de[y])
swap(x,y);
int dh = de[x] - de[y];
int kmax = log2(dh);
for (int k = kmax; k >= 0; k --){
if ((dh >> k) & 1)
x = fa[x][k];
}
if (x == y) return x;
kmax = log2(de[x]);
for (int k = kmax; k >= 0; k --) {
if (fa[x][k] != fa[y][k]) {
x = fa[x][k];
y = fa[y][k];
}
}
X = x,Y = y;
return fa[x][0];
}
int main(){
n = fr(),m = fr(),Q = fr();
nn = n;
int a,b,w;
memset(h,-1,sizeof h);
while (m --) {
a = fr(),b = fr(),w = fr();
add(a,b,w),add(b,a,w);
}
tarjan(1,-1);
dfs(1,0);
while (Q --) {
a = fr(),b = fr();
int p = LCA(a,b);
if (p <= n) {
fw(dis[a] + dis[b] - dis[p] * 2);
ch;
}
else {
int ans = dis[a] - dis[X];
ans += dis[b] - dis[Y];
int l = abs(s[X] - s[Y]);
int dm = min(l,stot[X] - l);
ans += dm;
fw(ans);
ch;
}
}
return 0;
}
广义圆方树
普通圆方树(也就是上面的狭义圆方树)只能解决仙人掌图上的问题,而广义圆方树可以将所有无向图转化为圆方树来处理
广义圆方树的性质:圆点方点相间,不存在说圆点和圆点相连,方点和方点相连的情况。
构造方法:
-
原图中的点被称为圆点
-
求得原图中所有点双连通分量,对每一个点双都新建一个节点,这类点被称为方点(这里将两个点一条边的情况也看作是点双)
-
删去原图中的边,令每一个圆点向包含该点的点双对应的方点连边
但是这样构建的时候,会有边的信息丢失(仙人掌图没有)
(虽然我没有写代码,但是别人的 \(blog\) 是这么写的)
好好好,写了代码了,在这里link,Tourist这道题
练习
今天的 \(A\) 题一直题目读不懂,然后去找了老师之后老师说了一遍也没有听懂,于是作罢,从第二题开始做,然后发现第二题是原题,就快速搞完到第三题。第三题是和昨天有点像的分层图,分层图很快的写完了,但是除了一点小问题,调了一个小时左右吧()
第三题搞完回过头搞第一题,然后还没来得及写完老师就讲了。按着郭总的写了一版但是没看懂,自己写了一版
A.守矢的关键路径
这个题目主要就是题目难懂,题目读懂了就很好做了,题目要求的就是有多少个点在 \(1\) 点到 \(n\) 点的最长路上面。
然后这个的做法就是从原点求一遍最短路,然后一开始存边的时候存一下反边,再从终点跑一遍最长路,如果这个点到原点的最长路和到终点的最长路的和等于原点到终点的最长路,就说明这个点在原点到终点的一条最短路上面。
把这个统计一下然后再输出就可以了。还有要注意的一点就是, \(dij\) 是没有办法直接跑最长路的!(郭总和潇潇都写了一次 \(dij\) 最长路,但是潇潇写 \(dij\) 的时候写错了,所以答案对了,但是郭总写的正确 \(dij\) 导致痛失分数,虽然是在第三题写的)
郭总这一题写的代码没看懂,就不贴了
struct node{
int v,w;
};
int n,m;
vector<node> e[N],fe[N];
int early[N],late[N];
int d1[N],d2[N];
bool flag[N];
void spfa1() {
memset(early,-0x3f,sizeof early);
memset(flag,0,sizeof flag);
queue<int> q;
early[1] = 0;
q.push(1);
while (q.size()) {
auto u = q.front();
q.pop();
flag[u] = false;
for (auto it : e[u]) {
int v = it.v,w = it.w;
if (early[v] < early[u] + w) {
early[v] = early[u] + w;
if (!flag[v]) {
flag[v] = true;
q.push(v);
}
}
}
}
}
void spfa2() {
memset(late,-0x3f,sizeof late);
memset(flag,0,sizeof flag);
queue<int> q;
late[n] = 0;
q.push(n);
while (q.size()) {
auto u = q.front();
q.pop();
flag[u] = false;
for (auto it : fe[u]) {
int v = it.v,w = it.w;
if (late[v] < late[u] + w) {
late[v] = late[u] + w;
if (!flag[v]) {
flag[v] = true;
q.push(v);
}
}
}
}
}
int main(){
n = fr(),m = fr();
for (int i = 1; i <= m; i ++) {
int a = fr(),b = fr(),w = fr();
e[a].push_back({b,w});
fe[b].push_back({a,w});
}
spfa1();
spfa2();
int ans = 0;
for (int i = 1; i <= n; i ++) {
if (early[i] + late[i] == early[n]) ans ++;
}
fw(ans);
return 0;
}
B.最大半连通子图
这一题就是一开始先缩个点,然后拓扑排序一下,统计一下每一个强连通分量作为终点的时候他所对应的最大半连通子图的数量和大小,最后再统计一遍就可以了。
这一个题目在 \(ACwing\) 的提高课里面做过
int n,m,cnt;
int mod;
vector<int> e[N],edge[N];
int dfn[N],low[N],timestamp;
stack<int> s;
bool flag[N];
int h[N],siz[N],id[N],d[N];
int cntt[N],con[N];
void tarjan(int u) {
dfn[u] = low[u] = ++timestamp;
s.push(u);
flag[u] = true;
for (auto v : edge[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u],low[v]);
} else if (flag[v]) low[u] = min(low[u],dfn[v]);
}
if (dfn[u] == low[u]) {
cnt ++;
while (s.size()) {
auto t = s.top();
s.pop();
flag[t] = false;
h[t] = cnt;
siz[cnt] ++;
if (t == u) break;
}
}
}
void topsort() {
int idx = 0;
queue<int> q;
for (int i = 1; i <= cnt; i ++) {
if (!d[i]) q.push(i);
}
while (q.size()) {
auto u = q.front();
q.pop();
id[++ idx] = u;
for (auto v : e[u]) {
d[v] --;
if (!d[v]) {
q.push(v);
}
}
}
}
int main(){
//freopen("qwq.in","r",stdin);
n = fr(),m = fr(),mod = fr();
for (int i = 1; i <= m; i ++) {
int a = fr(),b = fr();
edge[a].push_back(b);
}
for (int i = 1; i <= n; i ++) {
if (!dfn[i]) tarjan(i);
}
map<lwl,bool> s; // 标记这个边有没有
for (int i = 1; i <= n; i ++) {
int u = h[i];
for (int j : edge[i]) {
int v = h[j];
if (u == v) continue;
lwl hash = (lwl)u * N + v;
if (!s[hash]) {
s[hash] = 1;
e[u].push_back(v);
d[v] ++;
}
}
}
topsort();
for (int i = 1; i <= n; i ++) {
int u = id[i];
if (!cntt[u]) {
cntt[u] = 1;
con[u] = siz[u];
}
for (auto v : e[u]) {
if (con[v] < con[u] + siz[v]) {
con[v] = con[u] + siz[v];
cntt[v] = cntt[u];
} else if (con[v] == con[u] + siz[v]) {
cntt[v] += cntt[u];
cntt[v] %= mod;
}
}
}
int ans = 0,sum = 0;
for (int i = 1; i <= n; i ++) {
if (ans < con[i]) {
ans = con[i];
sum = cntt[i];
} else if (ans == con[i]) {
sum = (sum + cntt[i]) % mod;
}
}
fw(ans),ch;
fw(sum);
return 0;
}
C.Grass Cownoisseur
然后这一题一开始肯定是要缩点的,因为如果到了这个强连通分量里面其他的点肯定是要走一遍的,不走是傻子。
然后因为题目中说可以逆方向走一遍,我们就可以像昨天那道飞行航线还是啥一样建一个分层图,第一层就是没有用过反方向次数的点,第二层就是用过反方向次数的点。
然后这里记得要把后面新的点的 \(siz\) 用前面的赋值一下。一开始这个赋值的地方写错了,本来应该是 \(siz[i + cnt] = siz[i]\) ,结果不知道脑子怎么想的写的是 \(siz[i + cnt] = siz[cnt]\) 检查半天检查不出来。
最后跑一遍最长路就可以了,然后最长路不能用 \(dij\) !!!(郭总评价:我要放狂言,\(dij\) 死了)最后输出的时候因为前面连边的时候连过 \(u\) 和 \(v + cnt\) 了,所以直接输出 \(dis[h[1] + cnt]\) 就可以了。
还有要注意的一点是这里的原点所对应的值变了,不再是 \(1\) 了,所以不能直接用 \(1\) 来处理其它数据。
int n,m,cnt;
vector<int> edge[N],e[N],fedge[N];
int dfn[N],low[N],timestamp;
int siz[N],h[N];
int dis[N];
stack<int> s;
int st;
bool flag[N];
void tarjan(int u) {
dfn[u] = low[u] = ++timestamp;
s.push(u);
flag[u] = true;
for (auto v : e[u]) {
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[v],low[u]);
} else if (flag[v]) low[u] = min(low[u],dfn[v]);
}
if (dfn[u] == low[u]) {
++ cnt;
while (s.size()) {
auto t = s.top();
s.pop();
flag[t] = false;
h[t] = cnt;
siz[cnt] ++;
if (t == u) break;
}
}
}
void spfa() {
memset(flag,0,sizeof flag);
queue<int> q;
q.push(st),dis[st] = 0;
while (q.size()) {
auto u = q.front();
q.pop();
flag[u] = false;
for (auto v : edge[u]) {
if (dis[v] < dis[u] + siz[v]) {
dis[v] = dis[u] + siz[v];
if (!flag[v]) {
flag[v] = true;
q.push(v);
}
}
}
}
}
int main(){
//freopen("qwq.in","r",stdin);
n = fr(),m = fr();
for (int i = 1; i <= m; i ++) {
int a = fr(),b = fr();
e[a].push_back(b);
}
for (int i = 1; i <= n; i ++) {
if (!dfn[i]) tarjan(i);
}
for (int i = 1; i <= cnt; i ++) {
siz[i + cnt] = siz[i];
}
for (int i = 1; i <= n; i ++) {
int u = h[i];
for (auto j : e[i]) {
int v = h[j];
if (u == v) continue;
edge[u].push_back(v);
edge[u].push_back(v + cnt);
edge[v].push_back(u + cnt);
edge[u + cnt].push_back(v + cnt);
}
}
st = h[1];
spfa();
fw(dis[st + cnt]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号