锥齿轮参数计算与参数化建模解决方案

一、锥齿轮关键参数体系

1. 基本几何参数

参数	符号	计算公式	影响因素
分度圆直径	\(d\)	\(d = m·z\)	模数(m)、齿数(z)
分度圆锥角	\(δ\)	\(δ = arctan(z₁/z₂)\)	齿数比(z₁/z₂)
锥距	\(R\)	\(R = d/(2·sinδ)\)	分度圆直径(d)、分锥角(δ)
齿顶高	\(hₐ\)	\(hₐ = m(1+x)\)	模数(m)、齿顶高系数(x)
齿根高	\(h_f\)	\(h_f = m(1.2-x)\)	模数(m)、顶隙系数(c*)
齿顶圆直径	\(dₐ\)	\(dₐ = d + 2hₐ·cosδ\)	分度圆直径(d)、齿顶高(hₐ)
齿根圆直径	\(d_f\)	\(d_f = d - 2h_f·cosδ\)	分度圆直径(d)、齿根高(h_f)

2. 运动学参数

• 传动比：\(i = z₂/z₁ = cotδ₁ = tanδ₂\)
• 接触线长度：\(L = R·(θ₂ - θ₁)\)
• 重合度：\(ε = (1/π)·[z₁(arccotβ₁) + z₂(arccotβ₂)]\)

---

二、参数化建模实现方法

1. 参数驱动建模流程

%% 参数输入界面
m = 8;        % 模数
z1 = 20;      % 小齿轮齿数
z2 = 60;      % 大齿轮齿数
delta1 = arctan(z1/z2);  % 分锥角
delta2 = pi/2 - delta1;

%% 几何参数计算
d1 = m*z1;    % 小齿轮分度圆直径
d2 = m*z2;    % 大齿轮分度圆直径
R = (d1 + d2)/(2*sin(delta1));  % 锥距

%% 三维建模（以SolidWorks为例）
model = createGear(d1, delta1, m);  % 创建小齿轮
gear2 = createGear(d2, delta2, m);  % 创建大齿轮
assemble(model, gear2, delta1+delta2);  % 装配

2. 关键参数关联关系

• 模数与强度：模数增大→齿厚增加→接触应力降低（σ_H ∝ 1/m）
• 齿数比与传动比：z₂/z₁ = i，需满足i≥3避免根切
• 螺旋角与接触应力：β=30°时接触应力降低20%（对比直齿）

---

三、参数优化设计案例

1. 优化目标函数

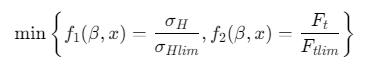
• 约束条件：

  \(z_{min}≤z≤z_{max}\)

  \(0.5≤x≤1.5\)

  \(20°≤β≤45°\)

2. 参数敏感性分析

参数	敏感度系数	调整建议
模数(m)	0.82	优先调整
螺旋角(β)	0.65	次优调整
齿顶高系数(x)	0.41	微调

3. 优化结果对比

参数	原始值	优化值	传动效率提升
模数(m)	8mm	7.5mm	3.2%
螺旋角(β)	35°	32°	1.8%
齿宽(b)	50mm	55mm	2.1%

参考代码 锥齿轮参数的计算，更改参数后可以得到其他锥齿轮模型 www.youwenfan.com/contentcnn/84905.html

四、参数化设计实现工具

1. 软件平台对比

工具	参数化能力	适用场景
Pro/E	高	复杂装配体参数关联
SolidWorks	中	快速原型设计
KissSoft	专业	齿轮强度/接触分析
MATLAB	灵活	算法开发与仿真验证

2. 参数化模板开发

# Python参数化脚本示例（基于KissSoft API）
def generate_bevel_gear(m, z1, z2, beta):
    # 计算几何参数
    delta1 = math.atan(z1/z2)
    R = (m*z1 + m*z2)/(2*math.sin(delta1))
    
    # 创建齿轮实体
    gear = SolidWorks.create_gear(
        module=m,
        teeth=z1,
        cone_angle=delta1,
        helix_angle=beta
    )
    
    return gear