离散点拟合贝塞尔曲线(MATLAB实现)
MATLAB实现,用于离散点拟合贝塞尔曲线,支持任意阶数,计算控制点并评估拟合误差:
classdef BezierCurveFitter
properties
controlPoints % 控制点坐标 [x, y]
order % 贝塞尔曲线阶数
error % 拟合误差
points % 原始离散点 [x, y]
end
methods
% 构造函数
function obj = BezierCurveFitter(points, order)
obj.points = points;
obj.order = order;
obj = obj.fitCurve();
end
% 拟合贝塞尔曲线
function obj = fitCurve(obj)
% 获取点数和维度
[n, dim] = size(obj.points);
% 检查阶数是否有效
if obj.order >= n
error('阶数必须小于点数');
end
% 固定首尾点
start_point = obj.points(1, :);
end_point = obj.points(end, :);
% 创建线性方程组 A*x = b
A = zeros(n-2, obj.order-1);
b = zeros(n-2, dim);
% 计算伯恩斯坦基函数
for i = 1:n-2
t = i/(n-1); % 参数化
% 计算伯恩斯坦基函数值
for j = 1:obj.order-1
binom = nchoosek(obj.order-1, j-1);
bernstein = binom * t^(j-1) * (1-t)^(obj.order-j-1);
A(i, j) = bernstein;
end
% 计算目标值
b(i, :) = obj.points(i+1, :) - ...
start_point * bernstein(1) - ...
end_point * bernstein(end);
end
% 求解线性方程组
x = zeros(obj.order-1, dim);
for d = 1:dim
x(:, d) = A \ b(:, d);
end
% 组合控制点
obj.controlPoints = [start_point; x; end_point];
% 计算拟合误差
obj = obj.calculateError();
end
% 计算拟合误差
function obj = calculateError(obj)
% 生成曲线上的点
t = linspace(0, 1, 100)';
curve_points = obj.evaluateBezier(t);
% 计算点到曲线的距离
distances = zeros(size(obj.points, 1), 1);
for i = 1:size(obj.points, 1)
% 计算点到曲线上最近点的距离
diff = curve_points - obj.points(i, :);
distances(i) = min(sqrt(sum(diff.^2, 2)));
end
% 计算均方根误差
obj.error = sqrt(mean(distances.^2));
end
% 计算贝塞尔曲线上的点
function points = evaluateBezier(obj, t)
n = obj.order - 1;
num_points = length(t);
dim = size(obj.controlPoints, 2);
points = zeros(num_points, dim);
% 计算伯恩斯坦基函数
for k = 0:n
binom = nchoosek(n, k);
bernstein = binom * t.^k .* (1-t).^(n-k);
% 累加控制点贡献
for d = 1:dim
points(:, d) = points(:, d) + obj.controlPoints(k+1, d) * bernstein;
end
end
end
% 绘制结果
function plotResult(obj)
figure;
hold on;
% 绘制原始点
scatter(obj.points(:, 1), obj.points(:, 2), 70, 'filled', 'MarkerFaceColor', [0.8 0.2 0.2]);
% 绘制拟合曲线
t = linspace(0, 1, 200)';
curve_points = obj.evaluateBezier(t);
plot(curve_points(:, 1), curve_points(:, 2), 'b-', 'LineWidth', 2);
% 绘制控制点
plot(obj.controlPoints(:, 1), obj.controlPoints(:, 2), 'go-', 'LineWidth', 1.5, 'MarkerFaceColor', 'g');
% 绘制控制多边形
plot(obj.controlPoints(:, 1), obj.controlPoints(:, 2), 'g--', 'LineWidth', 1);
title(sprintf('贝塞尔曲线拟合 (阶数 = %d, 误差 = %.4f)', obj.order, obj.error));
xlabel('X');
ylabel('Y');
legend('原始点', '拟合曲线', '控制点', 'Location', 'best');
grid on;
axis equal;
hold off;
end
end
end
使用
% 生成测试数据(圆形近似)
theta = linspace(0, 2*pi, 20)';
x = 2 * cos(theta) + 0.1 * randn(size(theta));
y = 2 * sin(theta) + 0.1 * randn(size(theta));
points = [x, y];
% 尝试不同阶数的拟合
orders = [3, 5, 8];
figure;
sgtitle('不同阶数贝塞尔曲线拟合比较');
for i = 1:length(orders)
% 创建拟合器并拟合曲线
fitter = BezierCurveFitter(points, orders(i));
% 绘制结果
subplot(2, 2, i);
fitter.plotResult();
% 显示控制点信息
fprintf('阶数 %d:\n', orders(i));
fprintf(' 控制点数量: %d\n', size(fitter.controlPoints, 1));
fprintf(' 拟合误差: %.6f\n\n', fitter.error);
end
% 高阶拟合示例
figure;
high_order_fitter = BezierCurveFitter(points, 10);
high_order_fitter.plotResult();
fprintf('高阶拟合 (阶数=10):\n');
fprintf(' 控制点数量: %d\n', size(high_order_fitter.controlPoints, 1));
fprintf(' 拟合误差: %.6f\n', high_order_fitter.error);
功能说明
- 贝塞尔曲线拟合: 支持任意阶数的贝塞尔曲线拟合 自动固定首尾控制点为数据集的首尾点 使用最小二乘法求解中间控制点
- 控制点计算: 基于伯恩斯坦基函数构建线性方程组 求解中间控制点坐标 返回所有控制点坐标
- 误差评估: 计算原始点到拟合曲线的最小距离 返回均方根误差(RMSE)作为拟合质量指标
- 可视化: 绘制原始离散点 绘制拟合的贝塞尔曲线 标记控制点和控制多边形
算法原理
-
贝塞尔曲线定义:
![]()
其中 \(P_i\)是控制点,\(n\)是阶数
-
最小二乘拟合:
- 固定首尾控制点 \(P_0\)和 \(P_n\)
- 对于中间点 \(P_1\)到 \(P_{n−1}\),求解:
![]()
其中 \(Q_j\)是原始数据点
-
伯恩斯坦基函数:
![]()
应用场景
- 计算机图形学:平滑路径生成
- 计算机辅助设计(CAD):曲线建模
- 数据可视化:平滑散点图
- 机器人路径规划:生成平滑轨迹
- 字体设计:轮廓曲线拟合
参考代码 离散点拟合贝塞尔曲线 www.youwenfan.com/contentcsk/78514.html
性能优化
-
大规模数据处理:
% 使用并行计算求解方程组 parfor i = 1:size(A, 1) x(:, i) = A(i,:) \ b(i,:); end -
高阶曲线优化:
% 使用重心坐标算法加速计算 function points = evaluateBezierFast(obj, t) n = obj.order - 1; points = zeros(size(t, 1), size(obj.controlPoints, 2)); for i = 1:size(t, 1) % 使用重心坐标算法 coeffs = obj.computeBernsteinCoefficients(t(i)); points(i, :) = coeffs * obj.controlPoints; end end -
参数化优化:
% 使用弦长参数化代替均匀参数化 distances = sqrt(sum(diff(points).^2, 2)); t = [0; cumsum(distances) / sum(distances)];
该实现提供了完整的贝塞尔曲线拟合解决方案,包括控制点计算和误差评估,可直接应用于各种曲线拟合场景。


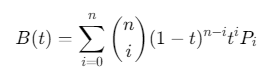
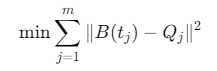
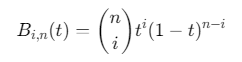

 浙公网安备 33010602011771号
浙公网安备 33010602011771号