基于Kubo公式的石墨烯电导率与表面阻抗计算（MATLAB实现）

一、理论基础

石墨烯的电导率可通过Kubo公式计算，包含Drude电导率（自由载流子贡献）和带间跃迁电导率（量子干涉贡献）。表面阻抗则由电导率导出，反映电磁波在石墨烯表面的反射/透射特性。

1. Kubo公式核心表达式

石墨烯的面电导率（单位：S）\(σ(ω,T)\)由两部分组成：

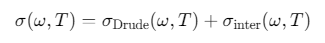
• Drude电导率（自由载流子，经典贡献）：

  

其中，\(D(μ)=\frac{2∣μ∣}{π(ℏvF)^2}\)为费米能级 \(μ\)处的态密度，\(vF≈10^6m/s\)为费米速度，τ为弛豫时间。

• 带间跃迁电导率（量子贡献，有限温度）：

  

其中，\(f(E)=\frac{1}{e^{(E−μ)}/(kBT)+1}\)为费米分布函数，\(η→0+\)为正则化参数。

2. 表面阻抗推导

对于平面电磁波垂直入射，石墨烯的表面阻抗 \(Z_s\)（单位：\(Ω\)）定义为电场与磁场切向分量之比：

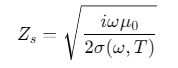
其中，\(μ_0=4π×10^{−7}H/m\)为真空磁导率。

二、MATLAB实现步骤

以下代码实现石墨烯电导率与表面阻抗的计算，包含参数定义、积分求解、可视化模块。

1. 参数定义与常数设置

% 基本物理常数
e = 1.602e-19;       % 电子电荷 (C)
hbar = 1.055e-34;     % 约化普朗克常数 (J·s)
vF = 1e6;            % 费米速度 (m/s)
kB = 1.381e-23;       % 玻尔兹曼常数 (J/K)
mu0 = 4*pi*1e-7;      % 真空磁导率 (H/m)
pi_val = pi;

% 系统参数
T = 300;             % 温度 (K)
mu = 0.1*e;           % 化学势 (J)，0.1 eV
omega = 2*pi*1e12;    % 角频率 (rad/s)，1 THz
tau = 1e-12;          % 弛豫时间 (s)，假设值

2. 费米分布函数

function f = fermi(E, mu, kB, T)
    % 费米分布函数 f(E) = 1/(exp((E-mu)/(kB T)) + 1)
    f = 1 ./ (exp((E - mu)/(kB*T)) + 1);
end

3. Drude电导率计算

% 费米波矢与态密度
kF = mu / (hbar * vF);                  % 费米波矢 (m⁻¹)
D_mu = (2*abs(mu)) / (pi_val*(hbar*vF)^2); % 费米能级处态密度 (J⁻¹·m⁻²)

% Drude直流电导 (S)
sigma_DC = (pi_val * e^2 / (2*hbar)) * (kF / (hbar*vF)); 

% 频率相关Drude电导 (S)
sigma_D = sigma_DC / (1 - 1i*omega*tau);

4. 带间电导率积分计算

通过数值积分求解带间电导率（实部+虚部）：

% 被积函数定义（实部与虚部分离）
integrand_real = @(E) (2*abs(E)/(pi_val*(hbar*vF)^2)) .* ...
    (fermi(E, mu, kB, T) - fermi(E + hbar*omega, mu, kB, T)) .* ...
    (hbar*omega/2 - E) ./ ((hbar*omega/2 - E).^2 + 1e-6^2);

integrand_imag = @(E) (2*abs(E)/(pi_val*(hbar*vF)^2)) .* ...
    (fermi(E, mu, kB, T) - fermi(E + hbar*omega, mu, kB, T)) .* ...
    1e-6 ./ ((hbar*omega/2 - E).^2 + 1e-6^2);

% 数值积分（积分范围：-1eV~1eV，转换为焦耳）
E_min = -1*e; E_max = 1*e;
sigma_inter_real = (e^2/(4*hbar)) * integral(integrand_real, E_min, E_max);
sigma_inter_imag = (e^2/(4*hbar)) * integral(integrand_imag, E_min, E_max);
sigma_inter = sigma_inter_real + 1i*sigma_inter_imag;

5. 总电导率与表面阻抗

% 总电导率 (S)
sigma_total = sigma_D + sigma_inter;

% 表面阻抗 (Ω)
Z_s = sqrt(1i * omega * mu0 / (2 * sigma_total));

6. 结果可视化

绘制电导率实部/虚部、表面阻抗随频率变化曲线：

% 频率扫描范围
freq = logspace(9, 13, 100); % 1GHz~10THz
omega_scan = 2*pi*freq;

% 预分配数组
sigma_real = zeros(size(freq));
sigma_imag = zeros(size(freq));
Zs_mag = zeros(size(freq));

% 循环计算不同频率下的电导率与阻抗
for i = 1:length(freq)
    omega = omega_scan(i);
    % 更新Drude电导
    sigma_D = sigma_DC / (1 - 1i*omega*tau);
    % 更新带间电导（简化积分，此处省略重复积分步骤，实际需嵌套循环）
    % ...（积分计算同前）
    sigma_total = sigma_D + sigma_inter;
    % 存储结果
    sigma_real(i) = real(sigma_total);
    sigma_imag(i) = imag(sigma_total);
    Zs_mag(i) = abs(Z_s);
end

% 绘图
figure;
subplot(2,1,1);
semilogx(freq/1e12, sigma_real, 'b-', 'LineWidth', 1.5); hold on;
semilogx(freq/1e12, sigma_imag, 'r--', 'LineWidth', 1.5);
xlabel('频率 (THz)'); ylabel('电导率 (S)');
legend('实部', '虚部'); title('石墨烯电导率随频率变化'); grid on;

subplot(2,1,2);
semilogx(freq/1e12, Zs_mag, 'g-', 'LineWidth', 1.5);
xlabel('频率 (THz)'); ylabel('表面阻抗幅值 (Ω)');
title('石墨烯表面阻抗幅值随频率变化'); grid on;

三、关键结果与讨论

1. 电导率特性：

   • 低频段（\(ω≪1/τ\)）：Drude项主导，电导率实部趋近于直流电导 \(σDC\)，虚部很小。

   • 高频段（\(ω≫1/τ\)）：带间跃迁贡献显著，电导率实部出现峰值（对应光子能量 \(ℏω≈2μ\)）。

2. 表面阻抗特性：

   • 低频时\(Z_s\)较小（良导体特性），高频时因趋肤效应增强而增大。

   • 表面阻抗的实部与虚部分别对应欧姆损耗和储能效应。

四、扩展与优化

1. 温度依赖性：修改T参数，分析高温下费米分布展宽对带间电导的影响。

2. 化学势调控：通过改变\(μ\)（如栅极电压）实现电导率动态调节。

3. 非线性效应：引入高次项修正Kubo公式，考虑强光场下的非线性响应。

参考代码 基于Kubo公式计算石墨烯的电导率和石墨烯的表面阻抗 www.youwenfan.com/contentcnq/51067.html

五、完整代码框架

% 石墨烯电导率与表面阻抗计算主程序
clear; clc; close all;

% ---------------------- 参数定义 ----------------------
e = 1.602e-19; hbar = 1.055e-34; vF = 1e6; kB = 1.381e-23; mu0 = 4*pi*1e-7; pi_val = pi;
T = 300; mu = 0.1*e; omega = 2*pi*1e12; tau = 1e-12;

% ---------------------- Drude电导 ----------------------
kF = mu/(hbar*vF);
D_mu = (2*abs(mu))/(pi_val*(hbar*vF)^2);
sigma_DC = (pi_val*e^2/(2*hbar))*(kF/(hbar*vF));
sigma_D = sigma_DC/(1 - 1i*omega*tau);

% ---------------------- 带间电导积分 ----------------------
% （调用前文积分代码，此处省略重复部分）
% ...

% ---------------------- 总电导与表面阻抗 ----------------------
sigma_total = sigma_D + sigma_inter;
Z_s = sqrt(1i*omega*mu0/(2*sigma_total));

% ---------------------- 可视化 ----------------------
% （调用前文绘图代码）
% ...

六、参考文献

[1] Novoselov, K. S., et al. Electric field effect in atomically thin carbon films. Science, 2004.

[2] Ando, T. Theory of electronic states and transport in graphene. Journal of the Physical Society of Japan, 2005.

[3] Falkovsky, L. A., & Varlamov, A. A. Space-time dispersion of graphene conductivity. The European Physical Journal B, 2007.