SFM（Structure from Motion）总结（二）

接下来我们介绍一下 Perspective SFM

与 affine SFM 不同，这里的 \(x_{ij}\) 无法直接表示为 \(A_iX_j+b_i\) 的形式，我们只能从它最根本的定义出发，即 \(x_{ij}=M_iX_j\) 得到，因此 Perspective SFM 需要求解的问题是通过已知的观测点信息估计相机矩阵 \(M\) 和 3D点 \(X\)。

对于每个观测值 \(x_{ij}\) 有 \(2\) 个坐标（因为图像点是二维的），所以总共有 \(2mn\) 个方程。

每个 \(3×4\) 的相机投影矩阵 \(M_i\) 有 \(12\) 个参数，但存在尺度等价性，所以每个 \(M_i\) 有 $11$ 个独立参数，\(m\) 个矩阵共有 \(11m\) 个参数；每个三维点 \(X_j\) 有 \(3\) 个坐标，\(n\) 个点共有 \(3n\) 个参数。

同时由于投影变换也存在投影歧义，如果相机未校准，相机和点只能恢复到一个 \(4×4\) 的投影变换，其自由度为15，因此我们共有 \(11m+3n-15\) 个未知数。

相当于我们需要用 \(2mn\) 个方程求解 \(11m+3n-15\) 个未知数。

像这样从一个投影变换恢复度量重建的问题称为自标定(self-calibration)

我们先解决第一个问题：如何从运动结构恢复到投影歧义，这里我们介绍 \(3\) 种方法。

代数方法(Algebraic approach)

这里以两视图为例，该方法共有 \(3\) 个步骤：

\(\bullet\) 从两视图中计算基础矩阵 \(F\)

\(\bullet\) 用 \(F\) 估计投影相机

\(\bullet\) 使用这些摄影机在3D中三角化和估计点

首先第一步我们需要计算基础矩阵 \(F\)，这里我们一般采用八点法进行计算，从至少 \(8\) 个点的对应关系中得到基础矩阵 \(F\)。

第二步是用 \(F\) 估计投影相机，由于存在投影歧义性，我们总可以应用一个投影变换 \(H\) ，使得经过投影变换后 \(M_1H^{-1}=[I,0]\)，即变换为规范透视相机的形式，而 \(M_2H^{-1}=[A,b]\)，这种变换有助于简化相机投影矩阵的形式，以便于后续的计算和分析。

我们规定将一般的三维点记为 \(X_{ij}\)，用 \(X\) 表示;相机 1 和相机 2 对应的观测点分别记为 \(x\) 和 \(x'\)。

同时我们定义变换后的投影矩阵 $\tilde{M}_1 = M_1H^{-1}=[I\ 0] $ 和 \(\tilde{M}_2 = M_2H^{-1}=[A\ b]\)，同时 \(\tilde{X}=HX\)。由此得到 \(x=M_1X=M_1H^{-1}HX=[I,0]\tilde{X}\) 和 \(x'=M_2X=M_2H^{-1}HX=[A,b]\tilde{X}\) 。

我们可以把 \(x'=[A,b]\tilde{X}\) 进一步展开，其中 \(\tilde{X}\) 是齐次坐标的形式 \(\begin{bmatrix}\tilde{X}_1\\\tilde{X}_2\\\tilde{X}_3\\1\end{bmatrix}\)，通过矩阵运算得到 \(x'=A[I,0]\tilde{X}+b=Ax+b\) 。

基于此公式我们可以进一步进行推导，我们对 \(x'\) 和 \(b\) 进行叉积运算得到 \(x'×b=(Ax+b)×b=Ax×b\)。

然后我们对公式两边左乘一个 \(x'^T\)，得到 \(x'^T·(x'×b)=x'^T·(Ax×b)=0\)，从而得到 \(x'^T·(b×Ax)=0\)。

进一步，我们可以将叉乘写成矩阵形式，如图所示：

从而可以得到 \(x'^T[b_×]Ax=0\)，这种形式是不是很熟悉呢？回想基础矩阵的性质有 \(x'^TFx=0\)，所以我们能够得到 \(F=[b_×]A=b×A\)。

但是如果我们将 \(F\) 与 \(b\) 点乘，则有 \(Fb=[b_×]A·b=0\)，所以我们得到的 \(F\) 矩阵还应满足 \(Fb=0\) 这一条件。

由于基础矩阵 \(F\) 是奇异矩阵（singular），可以通过奇异值分解（SVD）来计算满足 \(Fb = 0\) 且 \(|b| = 1\) 的向量 \(b\) 的最小二乘解。

通过类似推导，还能得到 \(b^TF=0\) ，进一步补充了向量 \(b\) 与基础矩阵 \(F\) 的转置之间的关系。

那我们应该如何计算 \(A\) 呢？

首先我们定义 \({A}' = -[{b}_{\times}]F\)

然后我们验证 \([b_{\times}]A'\) 是否等于 \(F\) 。通过矩阵运算： \([b_{\times}]A'=-[b_{\times}][b_{\times}]F=-(bb^T-|b|^2I)F=-bb^TF+|b|^2F\)，由于 \(Fb=0\) 且 \(|b|=1\)，所以 \(-bb^TF+|b|^2F=0+1·F=F\)。

从而我们能够得出 \(A=A'=-[{b}_{\times}]F\)，这样我们就能计算出 \(A\) 了。

进一步，我们可以根据前面的计算结果，得到变换后的相机投影矩阵 \(\tilde{M}_1 = [I,0]\) 和 \(\tilde{M}_2 = [-[{b}_{\times}]F,b]\) 。

现在的问题是应该如何求解 \(b\) 呢？

回想一下对极几何中的一些性质，如图所示：

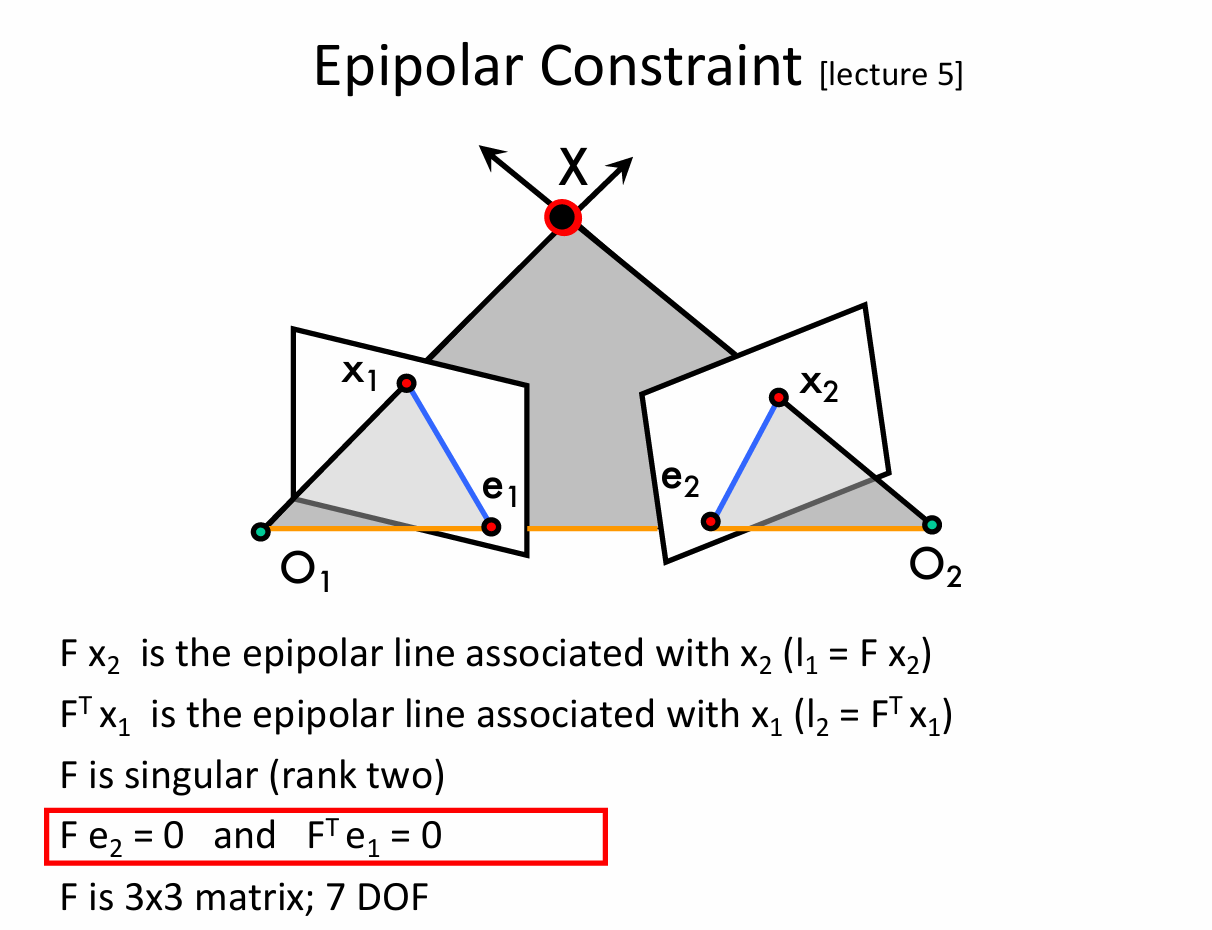
前面我们已知了 \(Fb=0\) 而 对极约束方程中恰好有 \(Fe_2=0\)，这告诉我们 \(b\) 其实是极点，所以我们又能够把相机投影矩阵写成如下形式：

\(\tilde{M}_1 = [I,0]\) 和 \(\tilde{M}_2 = [-[{e}_{\times}]F,e]\)

这样就完成了投影相机的估计。

第三步是使用这些摄影机在3D中三角化和估计点，我们已经知道了3D点和观测点之间的对应关系，还知道了投影相机矩阵，就能够通过奇异值分解求出3D点.

如果是在多视图中，我们可以从任意两个视图 \(I_k\) 和 \(I_h\) 出发，可以计算得到对应的投影矩阵 \(\tilde{M}_k\)、\(\tilde{M}_h\) 以及三维点 ，这些结果组合在一起就构成了多视图重建的结果。

因式分解(Factorization method)

与 affine SFM 中类似，这里不过多赘述。

以上两种方法都存在一定局限性：

对于因式分解方法，它假定所有的点都是可见的。但在以下情况该假设不成立：

\(\bullet\) 当出现遮挡时，部分点可能被其他物体遮挡而无法在图像中观测到。

\(\bullet\) 当在建立对应关系时失败，例如由于特征提取不准确或图像质量问题等，导致无法正确匹配不同视图中的点。

而代数方法主要适用于两视图的情况，对于更多视图的处理能力有限。

因此，人们提出了第三种方法：光束平差法（the bundle adjustment approach），该方法能够解决上述部分局限性。它可以在一定程度上处理遮挡和对应关系建立不准确等问题，通过优化所有相机参数和三维点位置来提高重建精度，是一种更综合和有效的优化方法。

光束平差法(Bundle adjustment)

光束平差法是一种用于优化结构和运动的非线性方法，其核心目标是最小化重投影误差。重投影误差的计算公式为 \(E(M,X) = \sum_{i = 1}^{m}\sum_{j = 1}^{n}D(x_{ij}, M_iX_j)^2\) 。其中，\(m\) 表示相机数量，\(n\) 表示三维点数量，\(x_{ij}\) 是图像上观测到的二维点，\({M}_i\) 是第 \(i\) 个相机的投影矩阵，\({X}_j\) 是第 \(j\) 个三维点，\(D(\cdot)\) 衡量了观测点 \(x_{ij}\) 和三维点 \({X}_j\) 通过投影矩阵 ${M}_i$ 投影到图像上的点之间的距离。

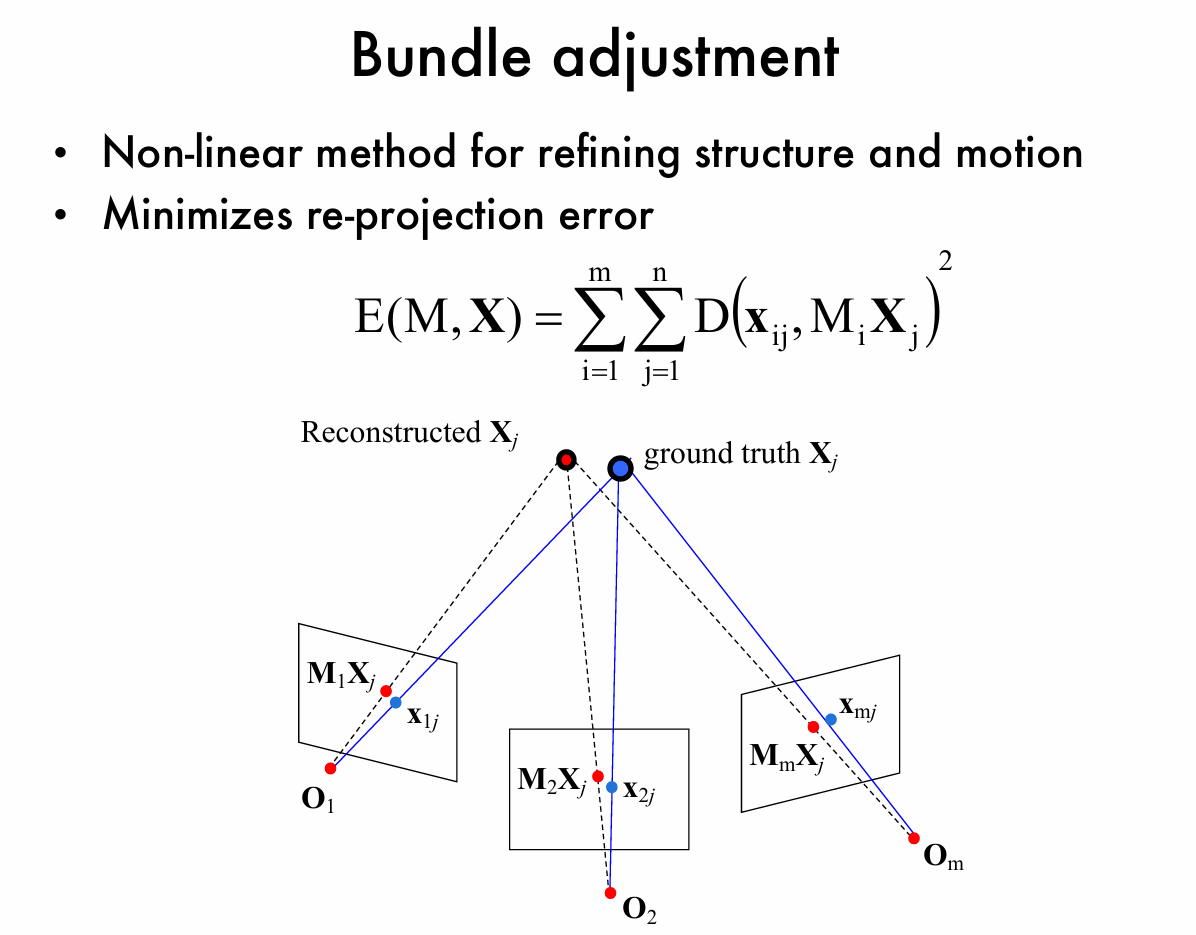
图中展示了多个相机\((\mathbf{O}_1\)、\(\mathbf{O}_2\)、\(\mathbf{O}_m\)）对三维点的观测情况。蓝色部分表示真实情况，即真实的三维点 \(\mathbf{X}_j\) 通过相机投影矩阵 \({M}_i\) 投影到图像上得到的点（如 \({M}_1{X}_j\)、\({M}_2{X}_j\)、\({M}_m{X}_j\) ）与图像上观测到的点 \({x}_{ij}\) 的理想对应关系。红色部分表示重建情况，即重建的三维点（Reconstructed \({X}_j\)） 投影到图像上的点与观测点之间存在偏差。光束平差法通过调整相机参数（投影矩阵 \({M}_i\) ）和三维点位置 \({X}_j\) ，来缩小这种偏差，从而最小化重投影误差。

为了解决这一问题，我们有两种求解办法：

\(\bullet\) 牛顿法（Newton Method）：是一种迭代算法，需要计算雅可比矩阵 \(J\) 和海森矩阵 \(H\)

\(\bullet\) 列文伯格 - 马夸尔特算法（Levenberg - Marquardt Algorithm）：同样是迭代算法，从初始解开始进行迭代计算。该算法具有以下特点：

1.如果初始解距离真实解较远，算法可能收敛较慢。

2.估计的解可能依赖于初始解。

3.与牛顿法不同，它不需要计算海森矩阵 \(H\) ，在一定程度上简化了计算过程。

最后我们总结一下光束平差法的优缺点以及应用场景：

优点

• 处理大量视图：能够处理大量的视图数据（Handle large number of views），在多视图的场景下具有较好的适用性。
• 处理缺失数据：可以应对数据缺失的情况（Handle missing data），在实际应用中，当部分数据由于各种原因（如遮挡等）缺失时，光束平差法仍能发挥作用。

局限性

• 大规模最小化问题：存在大规模的最小化问题，因为随着视图数量的增加，需要优化的参数也会相应增多），这会导致计算复杂度大幅上升。
• 依赖良好初始条件：需要一个较好的初始条件，如果初始值设置不合理，可能会导致算法收敛缓慢甚至无法收敛到最优解。

应用场景

• 作为SfM的最终步骤：通常被用作运动恢复结构的最后一步之后。
• 提供初始解：分解法或代数法可以为光束平差法的优化问题提供一个初始解，在此基础上，光束平差法通过迭代优化来进一步提高重建的精度。

自标定(Self - calibration)

定义：自标定是从透视（或仿射）重建中恢复度量重建的问题。在计算机视觉的三维重建中，透视（或仿射）重建通常能得到物体的形状和结构，但缺乏真实的尺度和度量信息；而度量重建则能提供具有真实尺度和几何度量的三维模型，自标定的目标就是在没有外部标定设备的情况下，从前者恢复出后者。

方法：可以通过对相机做出一些假设来进行相机自标定。这些假设可能涉及相机的内参特性，例如假设相机的焦距固定、图像传感器的像素是正方形等，基于这些假设来推导出相机的内参和外参，从而实现自标定。更具体的方法有：

单视图度量约束法：使用单视图度量约束(single - view metrology constraints)，该方法利用单幅图像中的一些几何度量信息，例如平行线、相似三角形等关系，来对相机进行自标定。

直接法（基于 Kruppa 方程）：对于两个视图的情况，采用直接法(Direct approach)，即基于 Kruppa 方程（Kruppa Eqs） 。Kruppa 方程建立了两个视图之间的内参关系，通过求解这些方程可以得到相机的内参，从而实现自标定。

代数法：通过代数方法(Algebraic approach)来进行相机自标定。通常涉及到对相机投影模型的代数运算和推导，利用多视图之间的几何关系建立代数方程，进而求解相机参数。

分层法：采用分层方法(Stratified approach)，该方法可能将自标定过程分为多个层次或阶段，逐步从低层次的几何信息（如仿射几何）过渡到高层次的度量几何信息，以实现相机的自标定。

后面几种做法较复杂这里不过多赘述，感兴趣请自行查阅相关资料。

以上就是对SFM相关内容的介绍，如有错误，请指正。