Tarjan算法和连通性相关(二)
上一篇博客我们介绍了强连通分量,本文我们继续学习与连通性有关的一些概念
割点
什么是割点?
对于一个无向图,如果把一个点删除后这个图的极大连通分量数增加了,那么这个点就是这个图的割点
我们画个图理解一下:
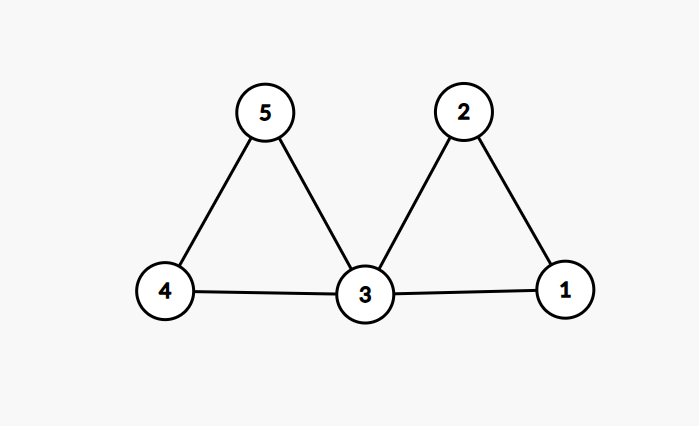
在这个图中,如果我们把 3 这个点给删除掉,那么这张图就会被拆分成两个部分,极大联通分量数就会增加,所以 3 这个点是割点,可以证明其他点都不是割点
怎么求割点?
与求强连通分量的方法类似,我们可以用Tarjan的思想去求割点
我们取图中的一个点,以它为起点开始做DFS,并维护DFS序,同时与求强连通分量的方法类似,我们也需要维护 low 数组
有了这两个信息,我们就能很快判断一个点是不是割点,因为对于某个顶点 u ,如果存在至少一个儿子顶点 v 使得 \(low[v]\) \(\ge\) $dfn[u] $ ,那么
u 点就是割点,因为删去 u 点,v 点无法到达祖先结点
但是对于搜索的起始点我们需要进行特殊考虑,仔细考虑一下会发现,如果该点只有一个儿子,那么该点就不是割点,如果有两个及以上的儿子,那么该点就是割点(读者可以画图想想这是为什么)
从而,我们利用Tarjan算法求出了割点,代码如下:
void Tarjan(int u, int father){
vis[u]=true;
low[u]=dfn[u]=++dfncnt;
int child=0;
for(auto v:g[u]){
if(!vis[v]){
child++;
Tarjan(v,u);
low[u]=min(low[u],low[v]);
if (father!=u&&low[v]>=dfn[u]&&!flag[u]){
flag[u]=true;
res++;
}
}
else if(v!=father){
low[u]=min(low[u],dfn[v]);
}
}
if (father==u&&child>=2&&!flag[u]){
flag[u]=true;
res++;
}
}
桥(割边)
什么是桥?
对于一个无向图,如果删掉一条边后图中的连通分量数增加了,则称这条边为桥或者割边,如图,红色的那条边就是桥
怎么求桥?
和求割点的思想差不多,只要将更新状态时改成 \(low[v]\) \(\gt\) $dfn[u] $ 就可以了,并且我们不需要考虑根节点的问题(读者也可以画图想想为什么)
代码如下:
void tarjan(int u, int fa) {
father[u]=fa;
low[u]=dfn[u]=++dfncnt;
for (auto v:g[u]) {
if (!dfn[v]) {
tarjan(v,u);
low[u]=min(low[u],low[v]);
if (low[v]>dfn[u]) {
isbridge[v]=true;
++cnt_bridge;
}
} else if(dfn[v]<dfn[u]&&v!=fa){
low[u]=min(low[u],dfn[v]);
}
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号