Transform详解及代码实践
第 1 阶段:Embedding 和位置编码详解
概述
Transformer 模型的第一步是将离散的 token(例如,单词的索引)转换为密集的向量表示。这个过程包括两个关键部分:
- Embedding 层:将整数索引映射到高维向量
- 位置编码:添加位置信息,因为自注意力机制是排列不变的
为什么需要 Embedding?
原始输入是离散的 token 索引,例如:
输入句子: "The cat sat on the mat"
Token: [2, 5, 8, 1, 2, 9] (假设 2 代表 "The")
这些整数索引本身没有任何数值意义。通过 Embedding,我们将其转换为一个连续的向量空间,其中语义相似的词有相似的向量表示。
Embedding 层的工作原理
Embedding 层本质上就是一个查找表:
词汇表大小: 10000
Embedding 维度: 512
┌─────────────────────────────────┐
│ Embedding 矩阵 (10000 × 512) │
├─────────────────────────────────┤
│ Token 0: [-0.5, 0.3, ..., 0.2] │ (padding token)
│ Token 1: [ 0.1, 0.8, ..., 0.5] │ (start token)
│ Token 2: [-0.2, 0.4, ..., 0.1] │ ("the")
│ Token 3: [ 0.6, 0.2, ..., 0.3] │ ("cat")
│ ...
│ Token 5: [ 0.3, 0.9, ..., 0.7] │
└─────────────────────────────────┘
查找过程:
输入: [2, 5]
输出: [
[-0.2, 0.4, ..., 0.1], (Token 2 的向量)
[ 0.3, 0.9, ..., 0.7] (Token 5 的向量)
]
关键参数
- 词汇表大小:模型能处理多少个不同的单词
- Embedding 维度(d_model):向量的维度,通常是 256, 512, 768 等
缩放因子 sqrt(d_model)
在论文中,embedding 被缩放 sqrt(d_model):
embeddings = embedding_matrix(input) * math.sqrt(d_model)
为什么? 这有助于保持 embedding 向量和位置编码的相对大小平衡。
位置编码的必要性
Transformer 的自注意力机制有一个重要的性质:它是排列不变的。
例子:
句子1: "The cat sat"
句子2: "sat cat The"
在自注意力中,这两个句子的处理方式是完全相同的!
这对于 NLP 来说是一个问题,因为单词的顺序至关重要。解决方案是在 embedding 中添加位置编码。
位置编码的设计
Transformer 论文使用的是固定的三角位置编码:
PE(pos, 2i) = sin(pos / 10000^(2i/d_model))
PE(pos, 2i+1) = cos(pos / 10000^(2i/d_model))
其中:
pos是 token 在序列中的位置(0, 1, 2, ...)i是维度索引(0, 1, 2, ..., d_model/2 - 1)d_model是模型维度
位置编码矩阵的样子
对于 d_model=8, max_seq_len=4:
维度 0 维度 1 维度 2 维度 3 维度 4 维度 5 维度 6 维度 7
位置 0: 0.00 1.00 0.00 1.00 0.00 1.00 0.00 1.00
位置 1: 0.84 0.54 0.07 1.00 0.01 1.00 0.00 1.00
位置 2: 0.91 -0.42 0.14 0.99 0.02 1.00 0.00 1.00
位置 3: 0.14 -0.99 0.21 0.98 0.03 1.00 0.00 1.00
为什么使用 sin 和 cos?
- 周期性:不同位置使用不同频率的波,这允许模型学习相对位置
- 可扩展性:对于任何序列长度都有定义,不需要为超长序列重新训练
- 数值稳定:值总是在 [-1, 1] 范围内
频率随维度变化
第 0 个维度(最低频率):
位置 0: sin(0) = 0
位置 1: sin(1) ≈ 0.84
位置 2: sin(2) ≈ 0.91
位置 100: sin(100) ≈ -0.51
第 7 个维度(最高频率):
位置 0: cos(0 * 10000^14/8) = 1.0
位置 1: cos(1 * 10000^14/8) = 1.0 (几乎没有变化)
位置 100: cos(100 * 10000^14/8) = 1.0
所以:
- 低维数使用低频,在长句子中变化缓慢(捕捉长期位置信息)
- 高维数使用高频,在短距离内快速变化(捕捉局部位置信息)
完整流程示例
输入: [2, 5, 8] (Token 索引)
步骤 1: Embedding
输出: [
[-0.5, 0.3, ..., 0.2], # Token 2 → 512 维向量
[ 0.3, 0.9, ..., 0.7], # Token 5
[ 0.1,-0.4, ..., 0.5] # Token 8
]
形状: (3, 512)
步骤 2: 缩放
输出: [
[-0.5 * sqrt(512), 0.3 * sqrt(512), ..., 0.2 * sqrt(512)],
...
]
缩放因子: √512 ≈ 22.6
步骤 3: 加入位置编码
位置 0 的编码: [0.0, 1.0, 0.0, 1.0, ...]
位置 1 的编码: [0.84, 0.54, 0.07, 1.0, ...]
位置 2 的编码: [0.91, -0.42, 0.14, 0.99, ...]
最终输出: [
Embedding[2] + PositionalEncoding[0],
Embedding[5] + PositionalEncoding[1],
Embedding[8] + PositionalEncoding[2]
]
形状: (3, 512)
学习嵌入向量
Embedding 矩阵中的权重在训练过程中会被学习。这意味着:
- 语义相似的词汇会学习得到相似的向量
- 向量会排列在一个连续空间中
- 线性关系可能会被学到:
向量("king") - 向量("man") + 向量("woman") ≈ 向量("queen")
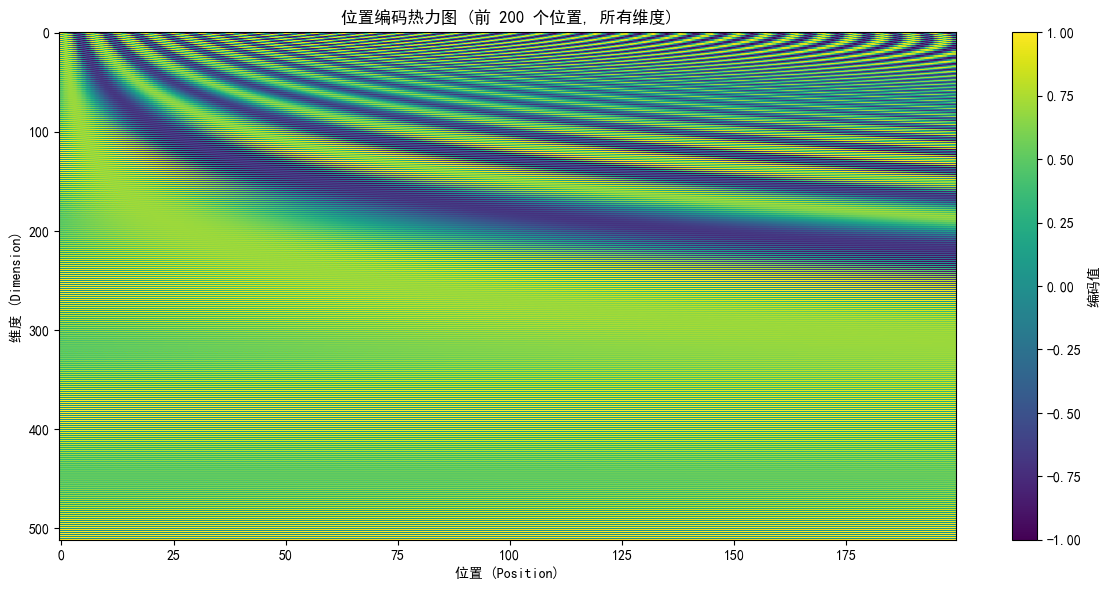
位置编码的可视化
在代码中运行 01_embedding.py 时,会生成一个热力图:
黑色区域:值接近 0
白色区域:值接近 1
灰色区域:值在 0 和 1 之间
观察:
- 低频维度(上部)变化缓慢
- 高频维度(下部)快速振荡
- 对角线模式表示不同位置的不同编码
代码实现详解
完整代码:
点击查看代码
"""
01_embedding.py - Embedding 和位置编码 (Positional Encoding)
Transformer 模型的第一步:将输入的离散 token 转换为密集向量表示
"""
import torch
import torch.nn as nn
import math
import matplotlib.pyplot as plt
class EmbeddingLayer(nn.Module):
"""
嵌入层:将整数 token 映射到密集向量空间
Args:
vocab_size: 词汇表大小
d_model: 模型维度(嵌入向量的维度)
"""
def __init__(self, vocab_size, d_model):
super(EmbeddingLayer, self).__init__()
# 创建一个 vocab_size × d_model 的矩阵
# 每个单词都对应一个 d_model 维的向量
self.embedding = nn.Embedding(vocab_size, d_model)
# 按照 Transformer 论文的建议,缩放嵌入向量
self.d_model = d_model
def forward(self, x):
"""
Args:
x: (batch_size, seq_len) 的整数 token 索引
Returns:
(batch_size, seq_len, d_model) 的嵌入向量,缩放因子为 sqrt(d_model)
"""
# embedding 的输出形状:(batch_size, seq_len, d_model)
embeddings = self.embedding(x) * math.sqrt(self.d_model)
return embeddings
class PositionalEncoding(nn.Module):
"""
位置编码 (Positional Encoding)
原理:由于 Transformer 模型中的自注意力机制是permutation-invariant的
(即不考虑单词顺序),为了保留位置信息,需要添加位置编码。
公式:
PE(pos, 2i) = sin(pos / 10000^(2i/d_model))
PE(pos, 2i+1) = cos(pos / 10000^(2i/d_model))
其中:
- pos 是单词在句子中的位置(0, 1, 2, ...)
- i 是维度的索引(0, 1, 2, ..., d_model//2 - 1)
- d_model 是模型的维度
"""
def __init__(self, d_model, max_seq_len=5000, dropout=0.1):
super(PositionalEncoding, self).__init__()
self.d_model = d_model
self.dropout = nn.Dropout(p=dropout)
# 创建位置编码矩阵 (max_seq_len, d_model)
pe = torch.zeros(max_seq_len, d_model)
# 位置索引 (0, 1, 2, ..., max_seq_len-1)
position = torch.arange(0, max_seq_len, dtype=torch.float).unsqueeze(1)
# 计算分母:10000^(2i/d_model)
# 这里我们先计算指数部分:2i/d_model
div_term = torch.exp(torch.arange(0, d_model, 2, dtype=torch.float) *
-(math.log(10000.0) / d_model))
# 应用正弦和余弦函数
# 偶数位置:使用 sin
pe[:, 0::2] = torch.sin(position * div_term)
# 奇数位置:使用 cos(当 d_model 是奇数时,最后一个位置可能只有 sin)
if d_model % 2 == 0:
pe[:, 1::2] = torch.cos(position * div_term)
else:
pe[:, 1::2] = torch.cos(position * div_term[:, :-1])
# 将位置编码注册为 buffer(不是参数,不需要训练)
# unsqueeze(0) 添加 batch 维度
self.register_buffer('pe', pe.unsqueeze(0))
print(f"✓ 位置编码初始化完成")
print(f" - 最大序列长度: {max_seq_len}")
print(f" - 模型维度: {d_model}")
print(f" - 位置编码矩阵形状: {pe.shape}")
def forward(self, x):
"""
Args:
x: (batch_size, seq_len, d_model) 的嵌入向量
Returns:
(batch_size, seq_len, d_model) 的向量 = 嵌入向量 + 位置编码
"""
# 获取序列长度
seq_len = x.size(1)
# 取出对应长度的位置编码 (1, seq_len, d_model)
pos_enc = self.pe[:, :seq_len, :]
# 将位置编码添加到嵌入向量中
x = x + pos_enc
# 应用 dropout
return self.dropout(x)
def demo_embedding_and_positional_encoding():
"""演示 Embedding 和 Positional Encoding 的效果"""
print("\n" + "="*80)
print("演示 1: Embedding 层")
print("="*80)
# 参数设置
vocab_size = 10000 # 词汇表大小
d_model = 512 # 模型维度
batch_size = 2 # 批次大小
seq_len = 4 # 序列长度
# 创建 embedding 层
embedding_layer = EmbeddingLayer(vocab_size, d_model)
# 创建随机的输入(token 索引)
input_tokens = torch.randint(0, vocab_size, (batch_size, seq_len))
print(f"\n输入 tokens (shape: {input_tokens.shape}):")
print(f" Batch 0: {input_tokens[0].tolist()}")
print(f" Batch 1: {input_tokens[1].tolist()}")
# 通过 embedding 层
embeddings = embedding_layer(input_tokens)
print(f"\n嵌入向量 (shape: {embeddings.shape}):")
print(f" Batch 0, Token 0 的前 10 个维度: {embeddings[0, 0, :10].detach().tolist()}")
print(f" 向量范数: {embeddings[0, 0].norm().item():.4f}")
print("\n" + "="*80)
print("演示 2: Positional Encoding")
print("="*80)
# 创建位置编码层
pos_encoding = PositionalEncoding(d_model=d_model, max_seq_len=5000, dropout=0.0)
# 添加位置编码
output = pos_encoding(embeddings)
print(f"\n添加位置编码后的输出 (shape: {output.shape}):")
print(f" Batch 0, Token 0 的前 10 个维度: {output[0, 0, :10].detach().tolist()}")
print(f" 向量范数: {output[0, 0].norm().item():.4f}")
# 展示位置编码的特性
print("\n位置编码的特性分析:")
print(f" 不同位置的编码向量是不同的:")
for i in range(seq_len):
print(f" 位置 {i} 的前 5 个维度: {output[0, i, :5].detach().tolist()}")
print(f"\n 相同维度在不同位置的变化:")
for dim_idx in [0, 1, 2]:
values = [output[0, pos, dim_idx].item() for pos in range(seq_len)]
print(f" 维度 {dim_idx}: {[f'{v:.4f}' for v in values]}")
# 可视化位置编码
print("\n" + "="*80)
print("演示 3: 位置编码可视化")
print("="*80)
# 生成位置编码矩阵用于可视化
pe_matrix = pos_encoding.pe[0, :200, :].detach().numpy()
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 黑体
plt.rcParams['axes.unicode_minus'] = False
# 绘制热力图
plt.figure(figsize=(12, 6))
plt.imshow(pe_matrix.T, cmap='viridis', aspect='auto')
plt.colorbar(label='编码值')
plt.xlabel('位置 (Position)')
plt.ylabel('维度 (Dimension)')
plt.title('位置编码热力图 (前 200 个位置, 所有维度)')
plt.tight_layout()
# 保存图表
save_path = r'c:\Users\13098\Desktop\Study\transformer\positional_encoding.png'
plt.savefig(save_path, dpi=100, bbox_inches='tight')
print(f"\n✓ 热力图已保存到: {save_path}")
plt.close()
if __name__ == "__main__":
demo_embedding_and_positional_encoding()
Embedding 层
class EmbeddingLayer(nn.Module):
def __init__(self, vocab_size, d_model):
super().__init__()
self.embedding = nn.Embedding(vocab_size, d_model)
self.d_model = d_model
def forward(self, x):
# x: (batch_size, seq_len)
# output: (batch_size, seq_len, d_model)
return self.embedding(x) * math.sqrt(self.d_model)
关键点:
nn.Embedding是 PyTorch 内置的查找表- 乘以
sqrt(d_model)是论文中的设计
位置编码层
class PositionalEncoding(nn.Module):
def __init__(self, d_model, max_seq_len=5000):
super().__init__()
pe = torch.zeros(max_seq_len, d_model)
# 位置索引:0, 1, 2, ..., max_seq_len-1
position = torch.arange(0, max_seq_len).unsqueeze(1)
# 频率:10000^(2i/d_model)
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
# 应用 sin 和 cos
pe[:, 0::2] = torch.sin(position * div_term) # 偶数维
pe[:, 1::2] = torch.cos(position * div_term) # 奇数维
self.register_buffer('pe', pe.unsqueeze(0))
def forward(self, x):
# x: (batch_size, seq_len, d_model)
seq_len = x.size(1)
# 加上相应长度的位置编码
return x + self.pe[:, :seq_len, :]
常见问题
Q: 为什么位置编码是加法而不是拼接?
A: 加法保持维度不变,允许模型灵活地混合内容和位置信息。
Q: 位置编码是否可以学习?
A: 原始论文使用固定的三角编码。后来的工作(如 RoPE)提出了相对位置编码,但固定编码仍然有效。
Q: 如果序列超过 max_seq_len 怎么办?
A: 模型可能会遇到问题。实际应用中可以:
- 增加 max_seq_len
- 使用相对位置编码
- 对长序列进行分割
下一步
现在你理解了如何将输入转换为向量表示。下一阶段我们将学习自注意力机制,这是 Transformer 的核心。
在自注意力中,这些嵌入向量将被用来计算 Query, Key, Value,从而学习 token 之间的关系。
第 2 阶段:自注意力机制详解
核心概念
自注意力(Self-Attention)是 Transformer 最核心的机制。它允许模型在处理每个 token 时,查看序列中的其他 token,学习它们之间的关系。
为什么需要注意力?
传统的序列模型(如 RNN)处理序列是逐步的:
输入: [a, b, c, d]
处理:
步骤1: 处理 a,隐藏状态 h1
步骤2: 处理 b,基于 h1,得到 h2
步骤3: 处理 c,基于 h2,得到 h3
步骤4: 处理 d,基于 h3,得到 h4
问题:
- 后面的 token 只能间接地看到前面的信息
- 处理很长的序列时,初始信息可能会被遗忘
注意力机制:允许每个 token 直接看到序列中的所有其他 token。
处理 c 时:
c 可以直接关注 a, b, d
并学习分别给予它们多少权重
缩放点积注意力(Scaled Dot-Product Attention)
这是 Transformer 中使用的注意力机制。
公式
Attention(Q, K, V) = softmax(Q * K^T / sqrt(d_k)) * V
其中:
Q(Query):查询向量,"我想找什么?"K(Key):键向量,"我是什么?"V(Value):值向量,"我的信息是什么?"d_k:Key 的维度,用于缩放
直观理解
例子:句子 "The cat sat on the mat"
(tokens: 0 1 2 3 4 5)
处理 token 1 ("cat") 时:
1. 计算 Query (q1) - 来自 "cat" 的嵌入
2. 计算所有 Key (k0, k1, k2, ...) - 所有 token 的嵌入
3. 计算相似度:q1 与 k0, k1, k2, ... 的点积
- q1 · k1 = 8.5 (高) - "cat" 关注自己
- q1 · k2 = 3.2 (中) - "cat" 关注 "sat"
- q1 · k5 = 1.1 (低) - "cat" 较少关注 "mat"
4. 归一化相似度(除以 sqrt(64))并应用 softmax
- softmax([8.5, 3.2, 1.1, ...]) = [0.45, 0.30, 0.15, ...]
5. 加权求和所有值:
output1 = 0.45 * v1 + 0.30 * v2 + 0.15 * v5 + ...
分步骤详解
步骤 1: 计算注意力分数
Q * K^T
输入:
Q: (seq_len, d_k) = (4, 64) - 4 个 token,每个 64 维
K: (seq_len, d_k) = (4, 64)
输出:
scores: (seq_len, seq_len) = (4, 4)
例子数值:
Token 0 Token 1 Token 2 Token 3
T0 [ 100.0 45.3 -20.1 12.5 ]
T1 [ 45.3 98.5 67.2 15.0 ] <- Token 1 的查询与所有 Key 的相似度
T2 [ -20.1 67.2 105.0 35.0 ]
T3 [ 12.5 15.0 35.0 92.0 ]
步骤 2: 缩放分数
scores / sqrt(d_k)
为什么缩放?
- 当 d_k 很大(如 64)时,点积会很大
- 大的输入值会导致 softmax 的梯度很小(梯度消失)
- 除以 sqrt(d_k) 可以稳定分布
例子:
sqrt(64) = 8
缩放前:[100.0, 45.3, -20.1, 12.5]
缩放后:[12.5, 5.66, -2.51, 1.56]
现在值在合理范围内,softmax 的梯度会更好。
步骤 3: 应用 Softmax
softmax(scores)
Softmax 将分数转换为概率(和为 1)。
缩放后的分数:[12.5, 5.66, -2.51, 1.56]
计算 softmax:
e^12.5 ≈ 270000
e^5.66 ≈ 287
e^-2.51 ≈ 0.08
e^1.56 ≈ 4.76
和 = 270000 + 287 + 0.08 + 4.76 ≈ 270292
Softmax = [270000/270292, 287/270292, 0.08/270292, 4.76/270292]
≈ [0.9989, 0.0011, 0.000, 0.000]
哇!Token 1 完全关注自己!这看起来不太对...
在实际 Transformer 中,计算过程是矩阵化的,结果会不同。
步骤 4: 与值相乘
attention_weights * V
输入:
attention_weights: (seq_len, seq_len) = (4, 4) (概率分布)
V: (seq_len, d_v) = (4, 64) (值向量)
输出:
output: (seq_len, d_v) = (4, 64)
例子:
假设 attention_weights[1] = [0.45, 0.30, 0.15, 0.10]
V 的各行是 [v0, v1, v2, v3]
output[1] = 0.45 * v0 + 0.30 * v1 + 0.15 * v2 + 0.10 * v3
多头注意力(Multi-Head Attention)
单一的注意力机制可能不足以捕捉所有类型的关系。解决方案:使用多个注意力"头"。
为什么使用多头?
示意:
单一注意力头:看 "red car",可能专注于颜色
多个注意力头:
头 1:专注于颜色 (红色)
头 2:专注于对象 (汽车)
头 3:专注于动作 (移动的)
头 4:专注于语法关系
组合所有头的输出,模型获得了丰富的理解。
架构
输入 x: (batch_size, seq_len, d_model) 例如 (2, 4, 512)
线性投影(分割为多头):
W_q @ x → (batch_size, seq_len, d_model)
→ reshape 和 transpose → (batch_size, num_heads, seq_len, d_k)
其中 d_k = d_model / num_heads
例如:512 / 8 = 64
并行执行多个注意力:
对于每个头:
Attention_i(Q, K, V) → (batch_size, seq_len, d_v)
拼接所有头:
(batch_size, seq_len, d_k) × 8 → (batch_size, seq_len, 512)
最终线性投影:
W_o @ concat → (batch_size, seq_len, d_model)
代码流程
# 输入
Q, K, V: (batch_size=2, seq_len=4, d_model=512)
# 线性投影
Q = W_q(Q) → (2, 4, 512)
K = W_k(K) → (2, 4, 512)
V = W_v(V) → (2, 4, 512)
# 分割为多头
num_heads = 8
d_k = 512 / 8 = 64
Q = reshape_and_transpose(Q) → (2, 8, 4, 64)
K = reshape_and_transpose(K) → (2, 8, 4, 64)
V = reshape_and_transpose(V) → (2, 8, 4, 64)
# 执行注意力(广播到所有 8 个头)
attn_output = Attention(Q, K, V) → (2, 8, 4, 64)
# 拼接
attn_output = reshape_and_transpose(attn_output) → (2, 4, 512)
# 最终投影
output = W_o(attn_output) → (2, 4, 512)
自注意力 vs 交叉注意力
自注意力 (Self-Attention)
Q, K, V 都来自同一个输入:
Q, K, V = input
用于:编码器中,token 关注同一句子中的所有 token
交叉注意力 (Cross-Attention)
Q 来自一个输入,K 和 V 来自另一个输入:
Q = decoder_input
K, V = encoder_output
用于:解码器中,decoder token 关注 encoder 的所有 token
因果掩码(Causal Mask)
在解码器中,我们使用因果掩码防止 token 在生成时看到未来的 token。
为什么需要?
在推理时,我们逐个生成 token:
第 1 步:生成 token 1(只能看到 token 1)
第 2 步:生成 token 2(只能看到 token 1 和 2)
第 3 步:生成 token 3(只能看到 token 1, 2, 3)
但在训练中,我们有完整的目标序列。为了保持一致,我们使用因果掩码:
步骤 1:计算所有 token 的注意力
步骤 2:应用掩码,将 token i 看到的 j > i 的权重设为 0
步骤 3:归一化
因果掩码矩阵
形状:(seq_len, seq_len)
值:0 表示看不到,1 表示能看到
seq_len = 4:
Token 0 Token 1 Token 2 Token 3
T0 [ 1 0 0 0 ]
T1 [ 1 1 0 0 ]
T2 [ 1 1 1 0 ]
T3 [ 1 1 1 1 ]
含义:Token 2 可以看到 Token 0, 1, 2,但看不到 Token 3。
应用掩码
if mask is not None:
# 将掩码为 0 的位置设为 -inf
scores = scores.masked_fill(mask == 0, float('-inf'))
# 对 [-inf 值的 softmax] = 0
softmax([-inf]) = 0
梯度流
注意力机制如何帮助梯度流动?
直接路径:
前向:token i 可以直接看到 token j(如果它们距离很远)
反向:token j 的梯度可以直接流向 token i
比较 RNN:
RNN 需要 |i - j| 步,距离越远,梯度越弱(梯度消失)
Transformer:
所有距离都是常数复杂度,梯度流动更均匀
计算复杂度
单个注意力头:
Q @ K^T: (seq_len, d_k) × (d_k, seq_len) = O(seq_len^2 * d_k)
Softmax: O(seq_len^2)
@ V: (seq_len, seq_len) × (seq_len, d_v) = O(seq_len^2 * d_v)
总体:O(seq_len^2 * d_model)
这比 RNN 的 O(seq_len * d_model^2) 对于长序列更好。
但也意味着对于非常长的序列,注意力会变得昂贵(平方复杂度)。
调试和理解注意力
查看注意力权重
output, attention_weights = attention(Q, K, V)
# attention_weights: (batch_size, num_heads, seq_len, seq_len)
# 查看第一个样本,第一个头
weights_first_head = attention_weights[0, 0]
print(weights_first_head)
# 输出:(4, 4) 矩阵,行和为 1
常见模式
-
对角线集中:token 主要关注自己
[[0.9, 0.05, 0.03, 0.02], [0.05, 0.85, 0.07, 0.03], [0.02, 0.08, 0.85, 0.05], [0.01, 0.03, 0.05, 0.91]] -
行为:前面的 token 关注后面的(例如,处理短语)
[[0.3, 0.7, 0.0, 0.0], [0.2, 0.4, 0.4, 0.0], [0.1, 0.2, 0.3, 0.4], [0.1, 0.1, 0.2, 0.6]] -
宽分布:均匀关注所有 token
[[0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25], [0.25, 0.25, 0.25, 0.25]]
下一步
现在你理解了自注意力如何工作。在下一个阶段,我们将学习如何将注意力与其他组件(前馈网络、残差连接、层归一化)组合成编码器层。
第 3 阶段:架构与编码器详解
编码器层的组件
Transformer 编码器层不仅仅是注意力机制。它是一个精心设计的组件组合:
┌─────────────────────────────────────────────────────┐
│ 编码器层 (EncoderLayer) │
├─────────────────────────────────────────────────────┤
│ 1. 多头自注意力 (Multi-Head Self-Attention) │
│ 2. 残差连接 (Residual Connection) │
│ 3. 层归一化 (Layer Normalization) │
│ 4. 前馈网络 (Feed-Forward Network) │
│ 5. 残差连接 (Residual Connection) │
│ 6. 层归一化 (Layer Normalization) │
└─────────────────────────────────────────────────────┘
前馈网络(Feed-Forward Network)
结构
位置级前馈网络在序列的每个位置独立应用相同的两层网络:
FFN(x) = max(0, x * W1 + b1) * W2 + b2
或用现代的 GELU 激活函数:
FFN(x) = GELU(x * W1 + b1) * W2 + b2
架构图
输入:(batch_size, seq_len, d_model)
│
▼
[线性层] d_model → d_ff (扩张)
W1: (d_model, d_ff)
│
▼
[激活函数] ReLU 或 GELU
│
▼
[Dropout]
│
▼
[线性层] d_ff → d_model (压缩)
W2: (d_ff, d_model)
│
▼
输出:(batch_size, seq_len, d_model)
维度示例
d_model = 512
d_ff = 2048 (通常是 4 * d_model)
输入:(batch_size=2, seq_len=4, d_model=512)
线性 1:(2, 4, 512) × (512, 2048) → (2, 4, 2048)
激活:(2, 4, 2048) → (2, 4, 2048) (应用 GELU)
线性 2:(2, 4, 2048) × (2048, 512) → (2, 4, 512)
输出:(2, 4, 512)
为什么这样设计?
-
维度扩张-压缩:
- 中间的宽层允许非线性变换在更大的空间中进行
- 压缩回 d_model 保持与其他层的兼容性
-
参数数量:
注意力:O(d_model^2) 参数 前馈:O(d_model * d_ff) ≈ 4 * d_model^2 参数 总体来看,前馈网络是主要的参数源。 -
激活函数的选择:
ReLU: max(0, x) - 简单但有 dead ReLU 问题 GELU: x * Φ(x) - 光滑,允许负值通过,效果更好
残差连接(Residual Connection)
概念
残差连接(也叫跳跃连接)允许信息绕过一个子层直接流向下一层:
不带残差:
输入 → [子层] → 输出
带残差:
输入 ───────────┐
│ │
▼ │
[子层] │
│ │
└──(+)──┘
│
▼
输出
输出 = 输入 + 子层(输入)
为什么需要残差连接?
-
梯度流动:
不带残差(深层网络): 梯度 = ∂Loss/∂输入 = ∂Loss/∂输出 × ∂输出/∂layer_n × ... × ∂layer_2/∂layer_1 问题:如果有 100 层,这是 100 个梯度的乘积。 如果每个梯度都 < 1,可能会导致梯度消失。 带残差: 梯度 = ∂Loss/∂输出 × (1 + ∂子层/∂输入) 由于有 "+1",即使 ∂子层 很小,梯度也不会完全消失。 -
网络深度:
不带残差:很难训练超过 50-100 层的网络 带残差:可以训练 1000+ 层的网络 -
初始化:
残差允许网络首先学习恒等函数 (输出 = 输入) 然后逐渐学习输出与输入之间的偏差。 这提供了一个好的初始点。
层归一化(Layer Normalization)
为什么需要归一化?
输入值的分布可能会随着网络的深度变化而改变。
这种现象叫做"内部协变量偏移" (Internal Covariate Shift)。
问题:
- 激活函数的有效范围被浪费
- 学习变得不稳定
- 需要更小的学习率
解决方案:在每一层之后进行归一化
批量归一化 vs 层归一化
批量归一化 (Batch Normalization):
沿着批次维度进行
E[x] = (1/batch_size) * Σ(x)
问题:对 NLP 不友好,会模糊句子中的位置信息
层归一化 (Layer Normalization):
沿着特征维度进行
E[x] = (1/d_model) * Σ(x)
优点:不依赖批次大小,适合变长序列
层归一化的计算
输入 x: (batch_size, seq_len, d_model)
对于每个 (batch_i, seq_j):
1. 计算该位置的 d_model 维向量的均值和方差
2. 归一化
3. 缩放和移位
数学:
LayerNorm(x) = γ * (x - μ) / √(σ² + ε) + β
其中:
μ = (1/d_model) * Σ(x) (均值)
σ² = (1/d_model) * Σ(x - μ)² (方差)
γ (gamma) 和 β (beta) 是可学习的参数
ε (epsilon) 是一个小值防止除以零
例子:
x = [2, 5, 8, 1, 3] (d_model = 5)
μ = (2 + 5 + 8 + 1 + 3) / 5 = 3.8
σ² = [(2-3.8)² + (5-3.8)² + ... ] / 5 ≈ 5.76
σ = 2.4
LayerNorm(x):
(2 - 3.8) / 2.4 = -0.75
(5 - 3.8) / 2.4 = 0.5
(8 - 3.8) / 2.4 = 1.75
(1 - 3.8) / 2.4 = -1.17
(3 - 3.8) / 2.4 = -0.33
结果:[-0.75, 0.5, 1.75, -1.17, -0.33]
Pre-norm vs Post-norm
论文使用的是 Post-norm:
[子层] → [LayerNorm] → 输出
更新的做法是 Pre-norm:
[LayerNorm] → [子层] → 输出
Pre-norm 优点:
- 更容易训练深层网络
- 不需要学习率预热
编码器层的完整流程
输入:x (batch_size, seq_len, d_model)
─────────────────────────────────────────
│ 子层 1: 多头自注意力 │
─────────────────────────────────────────
(1) 应用多头自注意力
attn_out = MultiHeadAttention(x, x, x)
形状: (batch_size, seq_len, d_model)
(2) 残差连接 + Dropout
x = x + Dropout(attn_out)
(3) 层归一化
x = LayerNorm(x)
─────────────────────────────────────────
│ 子层 2: 前馈网络 │
─────────────────────────────────────────
(1) 应用前馈网络
ffn_out = FFN(x)
形状: (batch_size, seq_len, d_model)
(2) 残差连接 + Dropout
x = x + Dropout(ffn_out)
(3) 层归一化
x = LayerNorm(x)
输出:x (batch_size, seq_len, d_model)
代码实现
class EncoderLayer(nn.Module):
def __init__(self, d_model, num_heads, d_ff, dropout=0.1):
super().__init__()
self.mha = MultiHeadAttention(d_model, num_heads, dropout)
self.ffn = PositionwiseFeedForward(d_model, d_ff, dropout)
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
self.dropout = nn.Dropout(p=dropout)
def forward(self, x, mask=None):
# 子层 1: 自注意力
x_norm = self.norm1(x)
attn_out, _ = self.mha(x_norm, x_norm, x_norm, mask=mask)
x = x + self.dropout(attn_out)
# 子层 2: 前馈
x_norm = self.norm2(x)
ffn_out = self.ffn(x_norm)
x = x + self.dropout(ffn_out)
return x
完整编码器(堆叠层)
┌──────────────────────────────────┐
│ 输入 (batch_size, seq_len, 512) │
└─────────────────────────────────┬┘
│
┌─────────────▼─────────────┐
│ 嵌入 + 位置编码 │
│ Output: (b, seq, 512) │
└─────────────┬─────────────┘
│
┌─────────────▼─────────────┐
│ 编码器层 1 │
│ (多头注意力 + 前馈) │
│ Output: (b, seq, 512) │
└─────────────┬─────────────┘
│
┌─────────────▼─────────────┐
│ 编码器层 2 │
│ (多头注意力 + 前馈) │
│ Output: (b, seq, 512) │
└─────────────┬─────────────┘
│
...
│
┌─────────────▼─────────────┐
│ 编码器层 6 │
│ (多头注意力 + 前馈) │
│ Output: (b, seq, 512) │
└─────────────┬─────────────┘
│
┌─────────────▼─────────────┐
│ 最终层归一化 │
│ Output: (b, seq, 512) │
└─────────────┬─────────────┘
│
┌─────────────▼─────────────┐
│ 输出 (batch_size, seq, 512)
└──────────────────────────┘
为什么堆叠多层?
浅层(第 1-2 层):学习低层特征
- 句法(词性、时态等)
- 局部语义
中层(第 3-4 层):学习中层特征
- 短语和子句的含义
- 句子结构
深层(第 5-6 层):学习高层特征
- 全局语义
- 完整的句子含义
编码器的应用
用于 NLP 任务:
1. 分类任务
输入:句子
输出:[cls_token_representation]
用途:分类,情感分析
例如:BERT
2. 提取任务
输入:句子
输出:所有 token 的表示
用途:命名实体识别,POS 标注
例如:BioBERT
3. 序列到序列的编码部分
输入:源语言句子
输出:源语言的编码表示
用途:机器翻译(编码器部分)
例如:mBART
调试和理解
打印中间值
def forward(self, x):
print(f"输入形状: {x.shape}, 值范围: [{x.min():.2f}, {x.max():.2f}]")
x_norm = self.norm1(x)
print(f"Norm 后: 值范围: [{x_norm.min():.2f}, {x_norm.max():.2f}]")
attn_out, _ = self.mha(x_norm, x_norm, x_norm)
print(f"注意力输出: [{attn_out.min():.2f}, {attn_out.max():.2f}]")
x = x + self.dropout(attn_out)
print(f"残差后: [{x.min():.2f}, {x.max():.2f}]")
return x
常见问题和解决方案
问题 1: 损失不下降
原因:学习率太高或太低
解决:调整学习率或使用学习率调度
问题 2: 梯度爆炸/消失
原因:网络太深或初始化不当
解决:使用梯度裁剪、层归一化、残差连接
问题 3: 出现 NaN
原因:除以零或数值不稳定
解决:检查 softmax(可能有大的正/负值)、添加 epsilon
问题 4: 验证精度不如训练精度
原因:过拟合
解决:增加 dropout、添加正则化、数据增强
下一步
现在你理解了单个编码器层的结构。下一个阶段,我们将添加解码器,形成完整的 Transformer 模型,可以处理序列到序列的任务。
第 4 阶段:完整 Transformer 模型详解
编码器-解码器架构
完整的 Transformer 是一个编码器-解码器模型,适用于序列到序列任务:
源语言 目标语言
(Source) (Target)
"Hello" ┐
"world" ├──→ [编码器] ──→ 编码表示 ──→ [解码器] ──→ "Bonjour"
│ "monde"
└──────────────────────────────────────────→ (交叉注意力)
编码器(Encoder)
编码器的工作是将源语言序列转换为一个丰富的表示。
输入:源语言句子 (整数 token)
[2, 5, 8, 1] (表示 "Hello world <pad>")
步骤 1: Embedding
形状: (batch_size, seq_len) → (batch_size, seq_len, d_model)
步骤 2: 位置编码
添加位置信息
形状: (batch_size, seq_len, d_model)
步骤 3: 6 层编码器层
每层包含:
- 多头自注意力
- 前馈网络
输入到第 1 层: (batch_size, seq_len, d_model)
输出:(batch_size, seq_len, d_model)
输出:编码表示
形状: (batch_size, seq_len, d_model)
包含了源语言句子的完整上下文
编码器的作用
编码器不进行任何翻译,只是进行编码:
"Hello" 的多个头的表示:
头 1(语法):[verb, singular, present, ...]
头 2(语义):[greeting, polite, ...]
头 3(实体):[person, singular, ...]
...
编码器确保这些信息被提取和融合到向量中。
解码器(Decoder)
解码器的工作是逐步生成目标语言句子。
解码器的特殊之处
解码器层包含三个子层,不是两个:
┌─────────────────────────────────────────────────────┐
│ 解码器层 (DecoderLayer) │
├─────────────────────────────────────────────────────┤
│ 1. 掩码多头自注意力 (Masked Multi-Head Attention) │
│ ↓ 残差 + 层归一化 │
│ 2. 交叉注意力 (Cross-Attention) │
│ ↓ 残差 + 层归一化 │
│ 3. 前馈网络 (Feed-Forward Network) │
│ ↓ 残差 + 层归一化 │
└─────────────────────────────────────────────────────┘
掩码自注意力 (Masked Self-Attention)
为什么需要掩码?
训练时:
有完整的目标序列 [token1, token2, token3]
但我们模拟推理时的情况:
- 生成 token1 时,只能看到 token1
- 生成 token2 时,只能看到 token1 和 token2
- 生成 token3 时,只能看到 token1, token2, token3
掩码(因果掩码):
┌───┬───┬───┐
│ 1 │ 0 │ 0 │
├───┼───┼───┤
│ 1 │ 1 │ 0 │
├───┼───┼───┤
│ 1 │ 1 │ 1 │
└───┴───┴───┘
应用掩码后:
token 3 对 token 1 的注意力权重 = 0
token 3 对 token 2 的注意力权重 = 0
token 3 对 token 3 的注意力权重 = 任意
交叉注意力 (Cross-Attention)
交叉注意力让解码器看到编码器的输出:
Query (Q): 来自解码器
"我现在在生成什么?"
(来自目标序列的表示)
Key (K) 和 Value (V): 来自编码器
"源语言是什么?"
(来自源语言的表示)
过程:
Q = 解码器当前位置的向量
K, V = 编码器的所有输出
Attention(Q, K, V) = softmax(Q * K^T / sqrt(d_k)) * V
这使解码器可以"查看"源语言的每个部分的相关性。
交叉注意力的可视化
源语言:The cat sat on the mat
目标语言:Le chat était assis sur le tapis (生成中)
当生成 "chat" (cat) 时:
Query (Q): "我在生成什么(关于 cat)"
Attention 权重:
The: 0.1 (不太相关)
cat: 0.7 (高度相关!)
sat: 0.1
on: 0.05
the: 0.03
mat: 0.02
加权组合所有源语言表示,得到一个包含相关信息的向量。
完整的前向传播
输入:
src: [2, 5, 8, 1] (源语言句子)
tgt: [1, 4, 7] (目标语言句子前缀,用于教师强制)
─────────────────────────────────────
│ 编码器部分 │
─────────────────────────────────────
1. 源语言 Embedding + 位置编码
输入:(batch=1, seq_len=4)
输出:(batch=1, seq_len=4, d_model=512)
2. 6 层编码器
输入:(1, 4, 512)
输出:(1, 4, 512) ← 保存以供解码器使用
─────────────────────────────────────
│ 解码器部分 │
─────────────────────────────────────
1. 目标语言 Embedding + 位置编码
输入:(batch=1, seq_len=3)
输出:(batch=1, seq_len=3, d_model=512)
2. 6 层解码器
对于每一层:
a. 掩码自注意力
Q, K, V = 解码器上一层的输出
b. 交叉注意力
Q = 解码器当前层的输出
K, V = 编码器的输出
c. 前馈网络
输入:(1, 3, 512) 和编码器输出 (1, 4, 512)
输出:(1, 3, 512)
─────────────────────────────────────
│ 输出层 │
─────────────────────────────────────
线性投影到词汇表
输入:(1, 3, 512)
权重:(512, vocab_size)
输出:(1, 3, vocab_size)
其中 vocab_size = 10000(例如)
每个位置得到一个长度为 vocab_size 的向量,
表示该位置生成每个 token 的概率。
生成过程(推理)
在训练时,我们有完整的目标序列。但推理时,我们需要逐个生成 token。
自回归生成
步骤 1:初始化
tgt_sequence = [<start>]
步骤 2:生成 token 1
编码源语言
encoder_out = encoder(src)
输入到解码器:tgt_sequence = [<start>]
解码器输出:logits for 位置 0
logits[0] = [0.2, 0.5, 0.1, 0.05, ...] (概率分布)
选择:argmax(logits[0]) = token 4
tgt_sequence = [<start>, 4]
步骤 3:生成 token 2
输入到解码器:tgt_sequence = [<start>, 4]
解码器输出:logits for 位置 0, 1
我们只关注位置 1:logits[1] = [0.1, 0.05, 0.8, 0.03, ...]
选择:argmax(logits[1]) = token 2
tgt_sequence = [<start>, 4, 2]
步骤 4:生成 token 3
继续...
步骤 5:停止条件
如果生成了 <end> token 或达到最大长度,停止
解码策略
不同的生成方式会得到不同的结果:
-
贪心解码 (Greedy Decoding)
next_token = argmax(logits)最快,但可能不是最优(局部最优)
-
束搜索 (Beam Search)
# 保持 k 个最有可能的候选序列 # 扩展每个候选,保留最好的 k 个 k = 3 # beam width更好的结果,但更慢
-
核采样 (Nucleus Sampling)
# 从高概率的 token 中随机采样 # 更多样的输出多样性更好,可能更自然
损失函数和训练
交叉熵损失
损失函数:CrossEntropyLoss
用于:分类问题(预测每个位置的 token)
计算:
logits: (batch_size, seq_len, vocab_size) 例如 (2, 5, 10000)
targets: (batch_size, seq_len) 例如 (2, 5) (真实 token)
对于每个位置,计算:
loss_i = -log(P(target_i))
其中 P(target_i) = softmax(logits_i)[target_i]
最终损失 = 平均所有位置和样本的损失
教师强制 (Teacher Forcing)
训练时:
我们有完整的目标序列
解码器在每一步都能"看到"正确的前缀
示例:
步骤 1:输入 [<start>],目标是 token 4
解码器看到 [<start>],学习生成 token 4
步骤 2:输入 [<start>, 4],目标是 token 2
解码器看到正确的历史,学习生成 token 2
步骤 3:...
推理时:
解码器看不到真实的目标序列
必须使用自己生成的 token
这会导致"曝露偏差" (exposure bias)
解决方案:
- Scheduled Sampling:逐渐减少教师强制
- 在训练中也使用生成的 token
超参数和模型大小
标准配置
| 模型大小 | d_model | num_heads | d_ff | num_layers | 参数数 |
|---------|---------|-----------|-------|-----------|--------|
| 小型 | 256 | 4 | 1024 | 2 | ~3M |
| 中型 | 512 | 8 | 2048 | 6 | ~50M |
| 大型 | 768 | 12 | 3072 | 12 | ~340M |
| Base | 768 | 12 | 3072 | 12 | ~110M |
原始论文(大型模型):
d_model = 512
num_heads = 8
d_ff = 2048
num_layers = 6
参数数 ≈ 65M
模型大小影响
参数更多:
✓ 更强的表达能力
✓ 更好的性能
✗ 更慢的训练和推理
✗ 需要更多数据
✗ 需要更多内存
实践建议:
- 从小型模型开始
- 逐步增加大小
- 根据验证性能调整
常见应用
1. 机器翻译 (Neural Machine Translation)
输入:英文句子
输出:中文句子
例如:Google Translate 的基础
2. 文本摘要 (Text Summarization)
输入:长文本
输出:简短摘要
编码器处理输入文本,解码器生成摘要
3. 对话系统 (Dialogue System)
输入:用户消息
输出:系统回复
单个 Transformer,输入和输出都是文本
4. 问答系统 (Question Answering)
输入:问题 + 文本
输出:答案范围
可以修改为分类问题
调试技巧
验证梯度流
# 检查梯度是否正常流动
for name, param in model.named_parameters():
if param.grad is None:
print(f"警告:{name} 没有梯度")
elif param.grad.abs().max() > 1:
print(f"警告:{name} 的梯度很大 ({param.grad.abs().max()})")
保存和加载模型
# 保存
torch.save(model.state_dict(), 'model.pt')
# 加载
model = Transformer(...)
model.load_state_dict(torch.load('model.pt'))
推理
model.eval() # 切换到评估模式
with torch.no_grad(): # 不计算梯度
output = model(src, tgt)
下一步
现在你理解了完整的 Transformer 模型。下一个阶段是实际应用:训练翻译模型并生成序列。
第 5 阶段:训练和应用指南
完整的训练流程
流程概览
┌──────────────────────────────────────────────────────┐
│ │
│ 数据准备 │
│ │
└──────────┬───────────────────────────────────────────┘
│
▼
┌──────────────────────────────────────────────────────┐
│ │
│ 模型初始化 │
│ │
└──────────┬───────────────────────────────────────────┘
│
▼
┌──────────────────────────────────────────────────────┐
│ │
│ 训练循环(多个 Epoch) │
│ │
│ ┌────────────────────────────────────────────┐ │
│ │ Epoch 1, Epoch 2, ..., Epoch N │ │
│ │ │ │
│ │ 对于每个 Batch: │ │
│ │ 1. 前向传播 │ │
│ │ 2. 计算损失 │ │
│ │ 3. 反向传播 │ │
│ │ 4. 优化器更新参数 │ │
│ │ 5. 更新指标 │ │
│ │ │ │
│ │ 验证: │ │
│ │ 检查验证损失 │ │
│ │ 保存最好的模型 │ │
│ └────────────────────────────────────────────┘ │
│ │
└──────────┬───────────────────────────────────────────┘
│
▼
┌──────────────────────────────────────────────────────┐
│ │
│ 推理和评估 │
│ │
└──────────────────────────────────────────────────────┘
数据准备
数据加载
# 1. 定义数据集类
class TranslationDataset(Dataset):
def __init__(self, source_file, target_file, vocab):
# 读取源和目标文件
self.src_sentences = read_file(source_file)
self.tgt_sentences = read_file(target_file)
self.vocab = vocab
def __getitem__(self, idx):
# 返回一对句子的 token 索引
src_tokens = self.vocab.encode(self.src_sentences[idx])
tgt_tokens = self.vocab.encode(self.tgt_sentences[idx])
return torch.tensor(src_tokens), torch.tensor(tgt_tokens)
# 2. 创建数据加载器
dataset = TranslationDataset(...)
dataloader = DataLoader(dataset, batch_size=32, collate_fn=collate_fn)
# 3. Collate 函数处理可变长度
def collate_fn(batch):
srcs, tgts = zip(*batch)
# 填充到相同长度
max_src_len = max(len(s) for s in srcs)
max_tgt_len = max(len(t) for t in tgts)
src_padded = torch.full((len(batch), max_src_len), pad_idx, dtype=torch.long)
tgt_padded = torch.full((len(batch), max_tgt_len), pad_idx, dtype=torch.long)
for i, (src, tgt) in enumerate(batch):
src_padded[i, :len(src)] = src
tgt_padded[i, :len(tgt)] = tgt
return src_padded, tgt_padded
词汇表
class Vocabulary:
def __init__(self):
self.word2idx = {'<pad>': 0, '<start>': 1, '<end>': 2, '<unk>': 3}
self.idx2word = {v: k for k, v in self.word2idx.items()}
self.idx = 4 # 下一个新 token 的索引
def add_word(self, word):
if word not in self.word2idx:
self.word2idx[word] = self.idx
self.idx2word[self.idx] = word
self.idx += 1
def encode(self, sentence):
# "hello world" → [5, 6]
tokens = []
for word in sentence.split():
if word in self.word2idx:
tokens.append(self.word2idx[word])
else:
tokens.append(self.word2idx['<unk>'])
return tokens
def decode(self, indices):
# [5, 6] → "hello world"
words = []
for idx in indices:
if idx in self.idx2word:
word = self.idx2word[idx]
if word not in ['<pad>', '<start>', '<end>']:
words.append(word)
else:
words.append('<unk>')
return ' '.join(words)
训练详解
前向和反向传播
def train_epoch(model, dataloader, optimizer, criterion, device):
model.train() # 启用 dropout 等
total_loss = 0
for batch_idx, (src, tgt) in enumerate(dataloader):
src = src.to(device) # (batch_size, src_seq_len)
tgt = tgt.to(device) # (batch_size, tgt_seq_len)
# 创建因果掩码(防止看到未来的 token)
tgt_len = tgt.size(1)
tgt_mask = create_causal_mask(tgt_len, device)
# tgt_mask: (1, 1, tgt_len, tgt_len)
# [[1, 0, 0, ...],
# [1, 1, 0, ...],
# [1, 1, 1, ...]]
# 清除梯度
optimizer.zero_grad()
# 前向传播
# 输入:src 和 tgt[:-1](排除最后一个 token)
# 目标:tgt[1:](排除第一个 token <start>)
logits = model(src, tgt[:, :-1], tgt_mask=tgt_mask[:, :, :-1, :-1])
# logits: (batch_size, tgt_seq_len-1, vocab_size)
# 计算损失
# 将二维变为一维便于计算交叉熵
loss = criterion(
logits.reshape(-1, logits.size(-1)), # (-1, vocab_size)
tgt[:, 1:].reshape(-1) # (-1,)
)
# 反向传播
loss.backward()
# 梯度裁剪(防止梯度爆炸)
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0)
# 优化器更新
optimizer.step()
# 记录损失
total_loss += loss.item()
if batch_idx % 100 == 0:
print(f"Batch {batch_idx}, Loss: {loss.item():.4f}")
return total_loss / len(dataloader)
学习率调度
# 选项 1:固定学习率
optimizer = torch.optim.Adam(model.parameters(), lr=1e-4)
# 选项 2:学习率衰减
scheduler = torch.optim.lr_scheduler.StepLR(
optimizer,
step_size=10, # 每 10 个 epoch 衰减一次
gamma=0.1 # 乘以 0.1
)
# 选项 3:预热 + 衰减(推荐用于 Transformer)
def get_linear_schedule_with_warmup(
optimizer,
num_warmup_steps,
num_training_steps
):
def lr_lambda(current_step):
if current_step < num_warmup_steps:
return float(current_step) / float(max(1, num_warmup_steps))
return max(0.0, float(num_training_steps - current_step) /
float(max(1, num_training_steps - num_warmup_steps)))
return torch.optim.lr_scheduler.LambdaLR(optimizer, lr_lambda)
# 使用
num_epochs = 100
num_training_steps = len(dataloader) * num_epochs
num_warmup_steps = len(dataloader) * 5 # 前 5 个 epoch 预热
scheduler = get_linear_schedule_with_warmup(
optimizer, num_warmup_steps, num_training_steps
)
# 在每个 batch 后更新
for epoch in range(num_epochs):
for batch in dataloader:
...
scheduler.step()
验证
def evaluate(model, dataloader, criterion, device):
model.eval() # 禁用 dropout
total_loss = 0
with torch.no_grad(): # 不计算梯度
for src, tgt in dataloader:
src = src.to(device)
tgt = tgt.to(device)
tgt_len = tgt.size(1)
tgt_mask = create_causal_mask(tgt_len, device)
logits = model(src, tgt[:, :-1], tgt_mask=tgt_mask[:, :, :-1, :-1])
loss = criterion(
logits.reshape(-1, logits.size(-1)),
tgt[:, 1:].reshape(-1)
)
total_loss += loss.item()
return total_loss / len(dataloader)
# 在每个 epoch 后调用
best_val_loss = float('inf')
for epoch in range(num_epochs):
train_loss = train_epoch(...)
val_loss = evaluate(...)
print(f"Epoch {epoch}: Train Loss {train_loss:.4f}, Val Loss {val_loss:.4f}")
if val_loss < best_val_loss:
best_val_loss = val_loss
torch.save(model.state_dict(), 'best_model.pt')
print(f"模型已保存,验证损失降低到 {val_loss:.4f}")
推理(生成翻译)
自回归生成
def generate_translation(model, src, max_len=30, device='cpu'):
"""
自回归地生成目标语言序列
"""
model.eval()
with torch.no_grad():
# 编码源语言
src = src.unsqueeze(0).to(device) # (1, src_len)
# 前向传播编码器
src_emb = model.src_embedding(src)
src_emb = model.src_pos_encoding(src_emb)
encoder_out = model.encoder(src_emb)
# 初始化目标序列(开始 token)
start_token = 1 # <start>
tgt = torch.full((1, 1), start_token, dtype=torch.long, device=device)
# 逐个生成 token
for step in range(max_len):
# 创建因果掩码
tgt_len = tgt.size(1)
tgt_mask = create_causal_mask(tgt_len, device)
# 解码器前向传播
tgt_emb = model.tgt_embedding(tgt)
tgt_emb = model.tgt_pos_encoding(tgt_emb)
decoder_out = model.decoder(
tgt_emb, encoder_out,
self_attn_mask=tgt_mask
)
# 输出层
logits = model.output_layer(decoder_out)
# 取最后一个位置的 logits
last_logits = logits[0, -1, :] # (vocab_size,)
# 生成下一个 token
# 方法 1: 贪心(选择概率最高的)
next_token = torch.argmax(last_logits, dim=-1, keepdim=True)
# 方法 2: 采样
# next_token = torch.multinomial(
# torch.softmax(last_logits, dim=-1),
# num_samples=1
# )
# 添加到序列
tgt = torch.cat([tgt, next_token.unsqueeze(0)], dim=1)
# 如果生成了结束 token,停止
if next_token.item() == 2: # <end>
break
return tgt[0]
束搜索(更高质量)
def beam_search(model, src, beam_width=3, max_len=30, device='cpu'):
"""
使用束搜索生成翻译(比贪心更好)
"""
model.eval()
with torch.no_grad():
# 编码
src = src.unsqueeze(0).to(device)
src_emb = model.src_embedding(src)
src_emb = model.src_pos_encoding(src_emb)
encoder_out = model.encoder(src_emb)
# 初始化候选序列
# 每个候选:(序列, 对数概率)
candidates = [
(torch.tensor([1], device=device), 0.0) # (序列, 对数概率)
]
for step in range(max_len):
next_candidates = []
for seq, log_prob in candidates:
# 跳过已结束的序列
if seq[-1].item() == 2: # <end>
next_candidates.append((seq, log_prob))
continue
# 扩展序列
seq = seq.unsqueeze(0).to(device)
tgt_len = seq.size(1)
tgt_mask = create_causal_mask(tgt_len, device)
tgt_emb = model.tgt_embedding(seq)
tgt_emb = model.tgt_pos_encoding(tgt_emb)
decoder_out = model.decoder(
tgt_emb, encoder_out,
self_attn_mask=tgt_mask
)
logits = model.output_layer(decoder_out)
last_logits = logits[0, -1, :] # (vocab_size,)
# 获取前 beam_width 个概率最高的 token
log_probs = torch.log_softmax(last_logits, dim=-1)
top_log_probs, top_tokens = torch.topk(
log_probs, beam_width
)
for top_log_prob, top_token in zip(top_log_probs, top_tokens):
new_seq = torch.cat([
seq.squeeze(0),
top_token.unsqueeze(0)
])
new_log_prob = log_prob + top_log_prob.item()
next_candidates.append((new_seq, new_log_prob))
# 选择概率最高的 beam_width 个序列
next_candidates.sort(key=lambda x: x[1], reverse=True)
candidates = next_candidates[:beam_width]
# 停止条件
if all(seq[-1].item() == 2 for seq, _ in candidates):
break
# 返回最好的候选
best_seq, _ = candidates[0]
return best_seq
评估指标
BLEU 分数(机器翻译)
from nltk.translate.bleu_score import corpus_bleu, sentence_bleu
def calculate_bleu(references, hypotheses, max_n=4):
"""
计算 BLEU 分数
references: 参考翻译列表 [["the", "cat"], ["a", "dog"], ...]
hypotheses: 生成的翻译列表 [["the", "cat"], ["a", "dog"], ...]
"""
score = corpus_bleu(
[[ref] for ref in references],
hypotheses,
weights=[1/max_n] * max_n
)
return score
# 使用
for src, ref in zip(src_sentences, ref_sentences):
hyp = generate_translation(model, src)
hyp_tokens = vocabulary.decode(hyp).split()
ref_tokens = ref.split()
bleu = sentence_bleu([ref_tokens], hyp_tokens)
其他指标
# 损失(来自验证集)
val_loss = evaluate(model, val_dataloader, criterion, device)
# 困惑度 (Perplexity)
perplexity = math.exp(val_loss)
# 准确率(token 级别)
def calculate_accuracy(model, dataloader, device):
correct = 0
total = 0
with torch.no_grad():
for src, tgt in dataloader:
logits = model(src.to(device), tgt[:, :-1].to(device))
predictions = torch.argmax(logits, dim=-1)
targets = tgt[:, 1:].to(device)
correct += (predictions == targets).sum().item()
total += targets.numel()
return correct / total
完整训练脚本示例
import torch
import torch.nn as nn
from torch.optim import Adam
from torch.utils.data import DataLoader
# 1. 加载数据
train_loader = DataLoader(train_dataset, batch_size=32, collate_fn=collate_fn)
val_loader = DataLoader(val_dataset, batch_size=32, collate_fn=collate_fn)
# 2. 创建模型
model = Transformer(
src_vocab_size=10000,
tgt_vocab_size=10000,
d_model=512,
num_layers=6,
num_heads=8,
d_ff=2048
).to(device)
# 3. 创建优化器和损失函数
optimizer = Adam(model.parameters(), lr=1e-4)
criterion = nn.CrossEntropyLoss(ignore_index=0) # padding token
# 4. 训练循环
num_epochs = 10
for epoch in range(num_epochs):
# 训练
train_loss = train_epoch(model, train_loader, optimizer, criterion, device)
# 验证
val_loss = evaluate(model, val_loader, criterion, device)
print(f"Epoch {epoch+1}/{num_epochs}")
print(f" Train Loss: {train_loss:.4f}")
print(f" Val Loss: {val_loss:.4f}")
# 保存最好的模型
if val_loss < best_val_loss:
best_val_loss = val_loss
torch.save(model.state_dict(), 'best_model.pt')
# 5. 评估
model.load_state_dict(torch.load('best_model.pt'))
test_loss = evaluate(model, test_loader, criterion, device)
print(f"Test Loss: {test_loss:.4f}")
# 6. 推理
model.eval()
with torch.no_grad():
for src in test_sources:
translation = generate_translation(model, src, device=device)
print(f"Source: {vocabulary.decode(src)}")
print(f"Translation: {vocabulary.decode(translation)}")
常见问题和解决方案
| 问题 | 原因 | 解决方案 |
|---|---|---|
| 训练损失不下降 | 学习率太小 | 增加学习率 (1e-3) 或使用学习率预热 |
| 梯度爆炸 | 初始化或学习率太高 | 梯度裁剪,减小学习率 |
| 梯度消失 | 网络太深或激活函数 | 检查激活函数,使用残差连接 |
| 验证损失增加 | 过拟合 | 增加 dropout,减小模型,数据增强 |
| NaN 损失 | 数值不稳定 | 检查 softmax,添加 epsilon,梯度裁剪 |
| 生成输出重复 | 模型学习了错误的模式 | 调整生成策略(束搜索),增加多样性 |
部署和优化
模型保存和加载
# 保存检查点
torch.save({
'epoch': epoch,
'model_state_dict': model.state_dict(),
'optimizer_state_dict': optimizer.state_dict(),
'loss': loss,
}, 'checkpoint.tar')
# 恢复训练
checkpoint = torch.load('checkpoint.tar')
model.load_state_dict(checkpoint['model_state_dict'])
optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
epoch = checkpoint['epoch']
推理优化
# 使用 torch.jit 编译模型(加速)
scripted_model = torch.jit.script(model)
# 量化(减少模型大小)
quantized_model = torch.quantization.quantize_dynamic(
model, {torch.nn.Linear}, dtype=torch.qint8
)
# 导出到 ONNX(跨框架兼容)
torch.onnx.export(
model, (src, tgt), "model.onnx",
input_names=['src', 'tgt'],
output_names=['output']
)
结论
现在你已经学会了:
- ✓ Transformer 的每个组件
- ✓ 完整的模型架构
- ✓ 训练和评估流程
- ✓ 推理和生成方法
下一步可以:
- 在真实数据集上训练(WMT, Europarl)
- 尝试不同的架构变体(Marian, Transformer-XL)
- 应用于其他任务(分类、摘要、QA)
- 探索多语言模型
祝学习愉快!🚀


 浙公网安备 33010602011771号
浙公网安备 33010602011771号