随笔分类 - algo
摘要： 
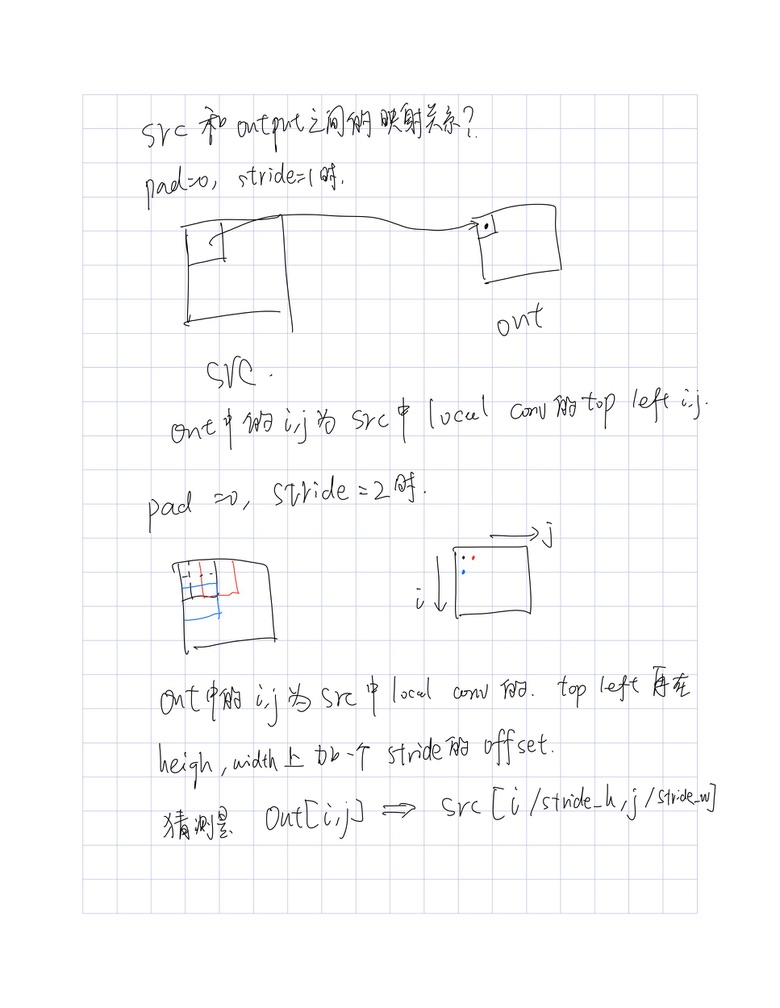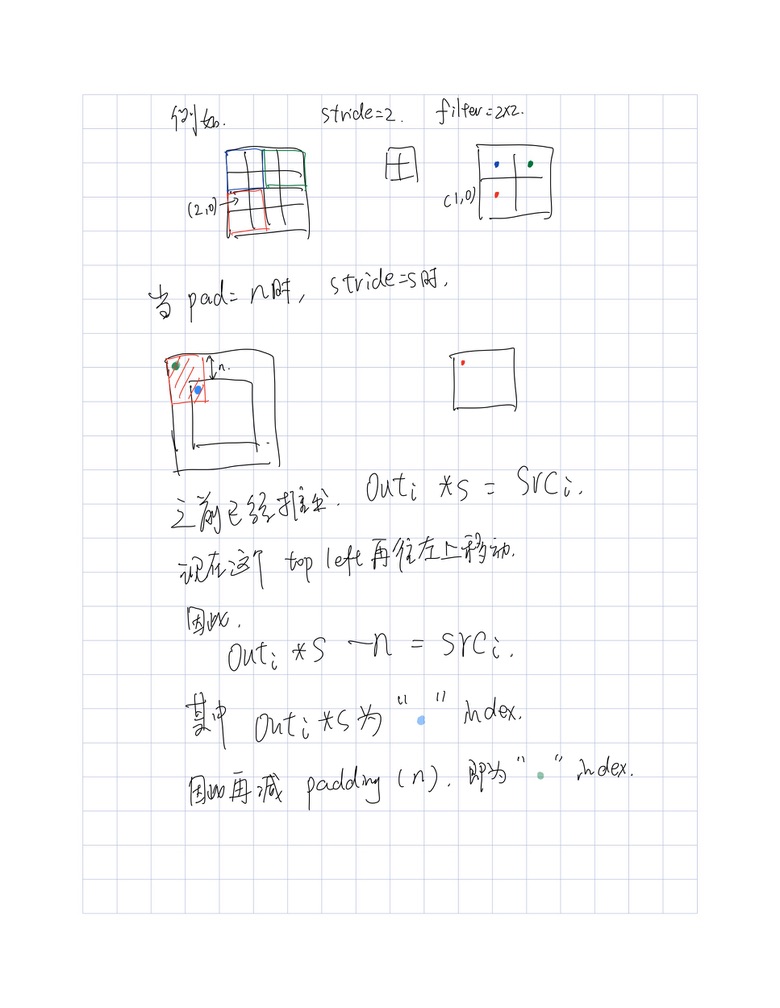
阅读全文
摘要：Untitled1 In [16]: import numpy as np np.set_printoptions(suppress=True) # 1,1,10,10; 1,1,2,2; 1,10,10; 1,10,10; 1,1,9,9 In [17]: N = 1 IC = 1 FH = FW
阅读全文
摘要：bit operations /2, *2 odd or even 实现mod 当计算\(a \mod b\) 且 b是\(2^n\)时，可以直接使用\(a \& (b-1)\)来计算\(a \mod b\)。 原理为：$a \mod b \(是\)a/b$的余数。 因为\(b=2^n\),\(
阅读全文
摘要：起因 邓俊辉的中序遍历二叉树采用了和前序遍历不同的循环检查方式，在前序遍历时使用stack非空检查，而在中序遍历时采用了while1检查。不便于迁移学习。 分析 视频地址： https://www.bilibili.com/video/BV1jt4y117KR?p=173 中序遍历时，根据规律每次进
阅读全文
摘要：问题定义 在区间[lo, hi)查找元素e search语义约定： 如果成功，返回e的位置；如果失败，返回不大于e的最大元素的位置 只有版本C符合语义约定 版本A到版本B的改进是为了平衡向左和向右走时的查找次数，使得在最坏情况下查找次数得到改善，而最好情况下版本A还是最好的（不过最好情况一般不会遇到
阅读全文
摘要：起因 在看邓俊辉在学堂在线上的数据结构课的时候，发现前序/中序的二叉树迭代遍历讲的都非常好，偏偏不讲后序。看了书上的讲解后也觉得一头雾水，尤其是需要去找左侧最深可见叶子节点那里，我基本需要背诵代码的逻辑，非常痛苦。 所以开始在网上找有没有更好理解的逻辑去写这个后序遍历。 发现 我发现，大多数讲解后序
阅读全文
