前缀和解题套路

概念

1D前缀和

目前见到的题目大多使用inclusive前缀和

[a1,a2   ,a3      ,....,an]

[a1,a1+a2,a1+a2+a3,....,a1+a2+...+an] 前缀和数组

差分数组

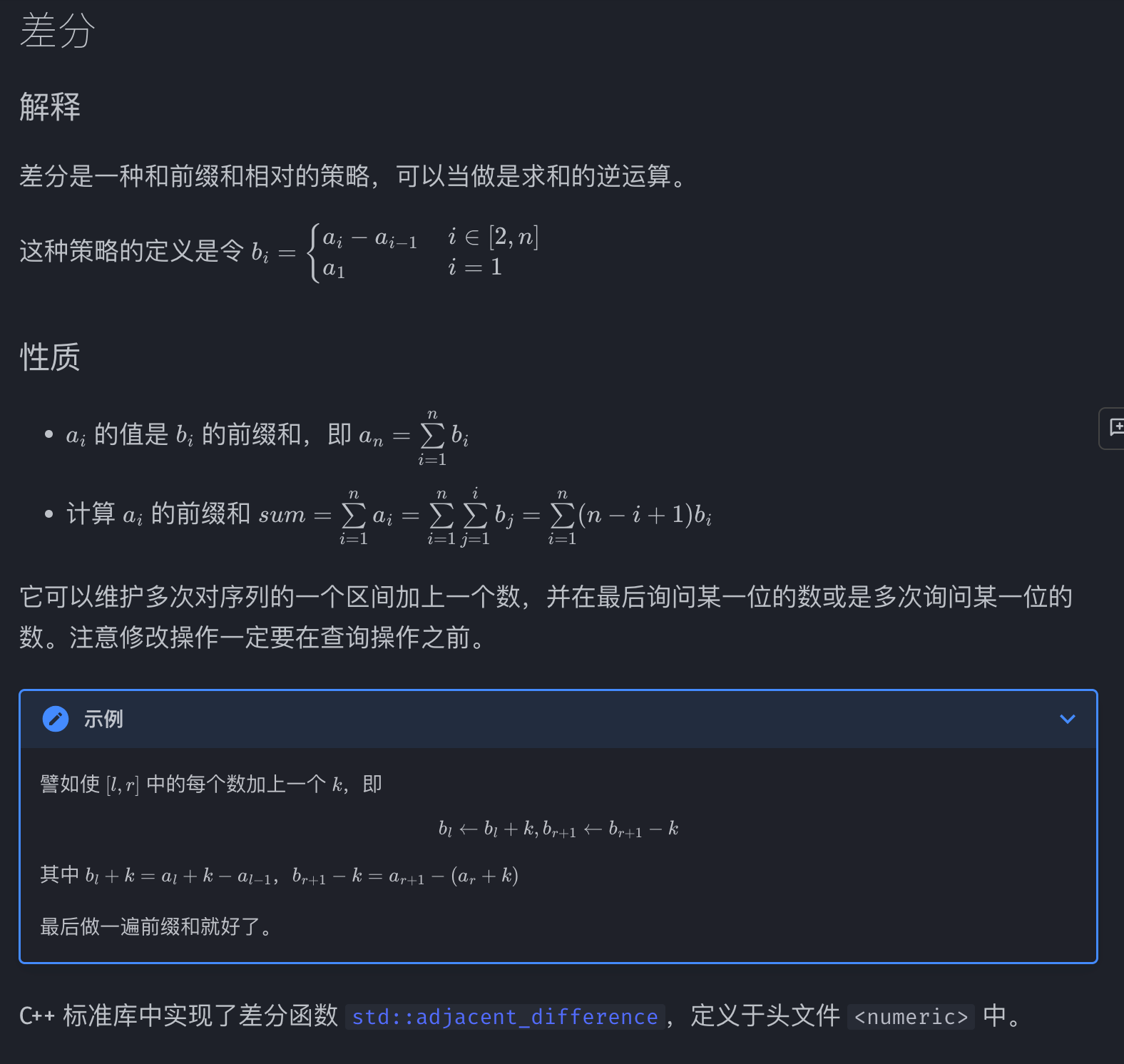
通过性质，可以使用的技巧

1. 对差分数组计算前缀和还原出原数组an
2. 对原数组an，[l,r]中每个数+k，原本每次+k操作需要O(n)。现在多次+k合并为一个O(n)

假设bn是an的差分数组，令 \(b_{l} \mathrel{{+}{=}} k, b_{r+1} \mathrel{{-}{=}} k, \text{如果} (r+1<=n)\)
对差分数组bn求前缀和
\(s1 = b1 = a1, s2 = b1+b2 = a1 + a2 - a1 = a2,...\)
\(s_l => b1 + b2 +... + b_l = a1 + a2 - a1 + a3 - a2 +...+ a_l - a_{l-1} + k => a_l + k\)
\(s_{l+1} = ... + b_{l} + b_{l+1} = a_l - a_{l-1} + k + a_{l+1} - a_l = a_{l+1} + k\)

可见，第\(a_l\)项开始会传播一个 +=k, 使得原数组从\(a_l\)开始，每项都 + k

同理，\(s_{r} = a_r + k\)
$s_{r+1} = b_{r+1} + b_{r} = a_{r+1}-a_r -k + a_r - a_{r-1} +k = a_{r+1} $

可以看出，第r+1项减掉k后，使得从第l项传播的k在第r+1项开始被抵消掉

因为，每次+k只针对\(b_l和b_{r+1}\)进行了算数操作，均为O(1)，因为多次+k操作后，还原数组an时，才是一个O(n)

2D前缀和

根据容斥原理可以写出该公式

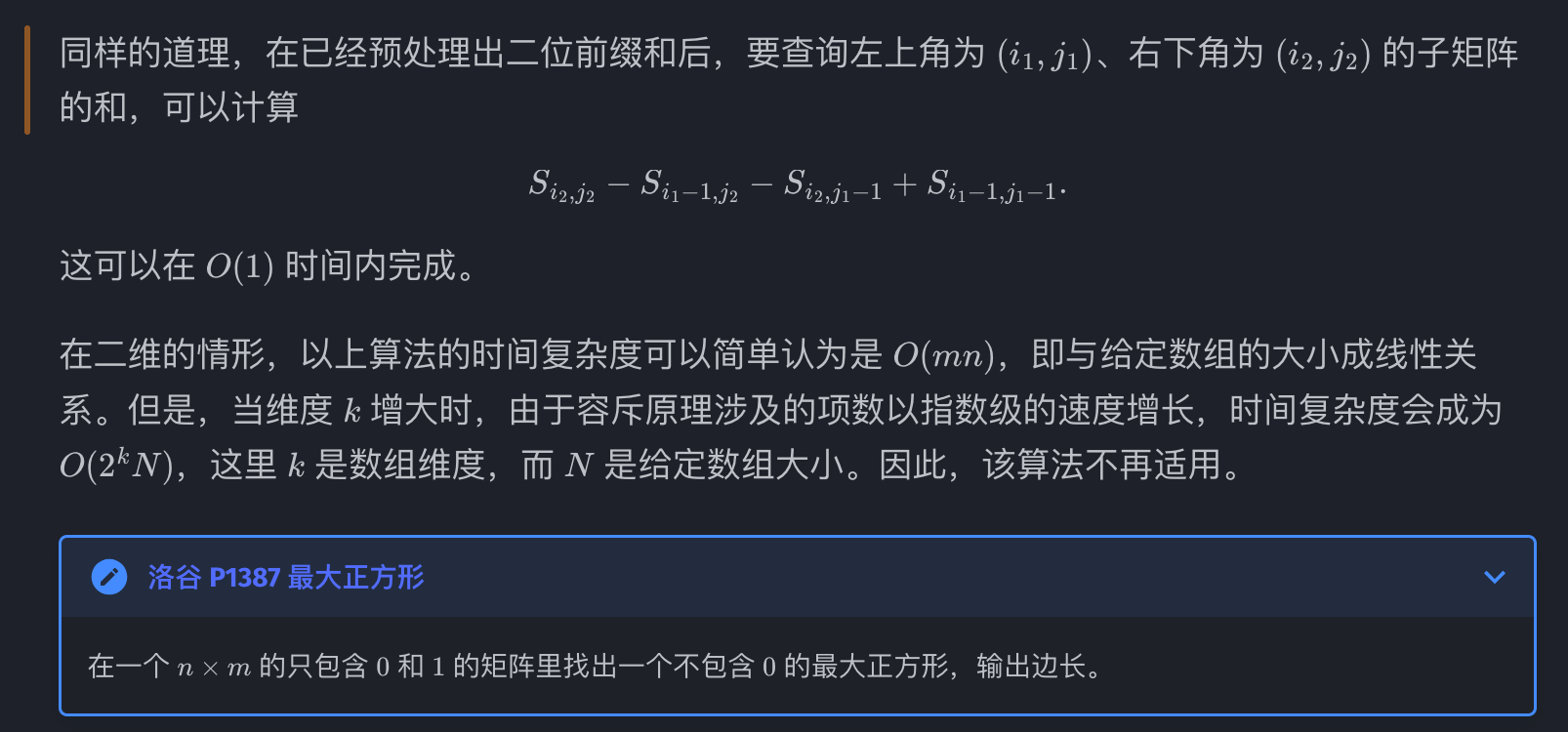
例题

https://leetcode.com/submissions/detail/1640381697/

常用技巧

前缀和数组中的前导0

求得前缀和数组后，[s1, s2,...] 因为我们一般处理子数组问题时，会围绕公式\(s_{j}-s_{i}\) 那么\(0<=i<j<n\) 那么，原数组中\(a1\)并没有被考虑. 例如\(s_{3}-s_{1} = a1+a2+a3-a1=a2+a3\)
所以，当我们有前导0时，前缀和数组为[s1=0,s2=a1,s3=a1+a2,...] ，则\(s_{3}-s_{1}=a1+a2-0=a1+a2\)我们就可以考虑到a1

代数转换

一般来说，当我们求出前缀和数组之后，围绕\(s_{j}-s_{i}\)满足特定条件思考问题，但是遍历j是O(n)，遍历i也是O(n)，那么写一个n^2的算法有时候不能满足问题规模。
那么如果用一些特定的代数转换就可以优化遍历索引i的过程。

例题1

https://leetcode.com/problems/continuous-subarray-sum/description/
在原数组an中找满足条件的子数组
条件1. 长度>=2
条件2. 子数组的和是k的倍数
那么，naive的做法就是分别迭代i和j，来检查a[i,...j]是否是k的倍数。

但是这里我们可以使用同余的概念来简化
$ \because (s_{j}-s_{i}) mod (k) = 0 $
$ \therefore $ 根据同余定理 \(s_{j}mod k = s_{i} modk\)
所以在每次迭代\(S_j\)时，记录\(S_j modk\)和\(j\)的值，查询是否有同余的被记录，检查（长度）索引差是否满足条件

例题2

https://leetcode.com/problems/subarray-sum-equals-k/description/
在原数组an中找出所有满足条件的子数组
条件1. 子数组和=k
即\(S_{j}-S_{i}=k => S_{j} -k = S_{i}\)
记录S_{i}的个数，然后迭代\(S_{j}\)时，查找\(S_{j}-k\)，计数器

例题3

https://leetcode.com/problems/contiguous-array/description/
求数组an中0和1数量相等的最长子数组
将0视为-1，那么子数组中0和1相等即-1和1数量相等，所以该子数组的和是0
就可以将问题转换为\(S_{j}-S_{i}=0;=>S_{j}=S_{i}\)
所以同样也是使用哈希记录已经遍历过的前缀和，然后每次更新子数组长度.
为了让子数组的长度尽量长，所以只在第一次找到前缀和=p时才记录，这样可以保证该记录对应的索引是最早的

反思前缀和数组的前导0问题

比如例题3，设前缀和数组为[s1,s2,s3,...]，当\(S_{j}=S_{i}\)时，表明\(a_{i+1} + a_{i+2} + ... + a_{j} = 0\)，即原数组an中索引i+1,i+2,...,j 构成的子数组的0和1的数量相同。因为0<=i,因此，1<=i+1，子数组无法包含a0。这里需要在前缀和数组中插入一个前导0.

有时候我在想，这里不一定插入的前导是0，要根据代数含义来决定

这里使用0来作为哨兵，与\(S_{j}\)匹配，表示[前导位置+1，j]的子数组含有相同数量的0和1

总结

这类使用代数转换的方法都是可以在代数上表示为等式关系的

不等关系问题

这类问题主要是构建在\(S_j - S_i < k\) 这个公式的基础上

例题1

https://leetcode.com/submissions/detail/1641180686/
设一个矩阵的左上角坐标为i,j. 右下角坐标为p,q
求\(max(S_{p,q} - S_{p,j-1} - S_{i-1,q} + S_{i-1,j-1} <= k)\)
如果分别枚举i,j,p,q，那么会得到一个O(n^4)复杂度的解法
那么先尝试优化到O(n^2xnlogn)这个级别

方法1

枚举左上角和右下角的横向坐标:i,p
这样我们就每次考察一个固定高度范围内的矩阵是否满足面积 <=k

然后我们将二维问题转换为一维问题，在考虑p,j之前，先将[i,p]每一列进行求和，得到一个以每一条纵向“柱”的数组，接下来，对这个数组求前缀和，那么问题就可以进一步到考虑[j,p]范围内\(S_p-S_j<=k\)的问题
因为迭代该前缀和数组时，需要考虑的问题是：是否存在\(S_j\)满足\(S_j>=S_p-k\)。如果\(S_j\)能够被有序地存放，那么就可以使用lower_bound恰好找到这个 \(>=S_p-k\)的\(S_j\)