时间分数阶微分方程数值求解
一、方法体系
1. 有限差分法(FDM)
-
原理:将Caputo导数离散为分数阶差分格式
![]()
-
实现步骤:
-
时间离散化:\(t_n=nτ\)
-
构造递推公式:
![]()
-
初始条件处理:\(y0=y(0)\)
-
2. 有限元法(FEM)
-
空间离散:采用Galerkin加权残量法
![]()
-
时间积分:结合Crank-Nicolson格式
% MATLAB代码框架 M = assemble_mass_matrix(); K = assemble_stiffness_matrix(); for n = 1:N b = M*y_prev + tau^alpha*(K*y_prev + F(t_n)); y_next = M\b; y_prev = y_next; end
3. 谱方法
-
适用场景:周期边界条件问题
-
实现要点:
- 基函数选择:Chebyshev多项式
- 导数计算:微分矩阵法
# Python示例(Chebyshev谱方法) from scipy.integrate import solve_ivp def cheb_diff_matrix(N): # 构造Chebyshev微分矩阵 ... D = cheb_diff_matrix(128)
4. 无单元Galerkin法(EFG)
-
优势:无需网格划分,适合复杂几何
-
关键步骤:
-
移动最小二乘近似构造形函数
-
弱形式离散:
![]()
-
系统矩阵组装
-
二、MATLAB实现方案
1. 内置工具箱方案
% 使用fracdiff工具箱
alpha = 0.75; % 分数阶阶数
tspan = [0, 2]; % 时间区间
y0 = 1; % 初始条件
f = @(t,y) -y + t^2; % 方程右侧
% 求解
[t,y] = fracdiff(f, tspan, y0, alpha);
% 可视化
plot(t,y);
xlabel('Time'); ylabel('Solution');
title(sprintf('\\alpha=%.2f Fractional ODE Solution', alpha));
2. 自定义有限差分实现
function y = fractional_ode_solver(alpha, tau, T, f, y0)
N = round(T/tau);
y = zeros(1,N+1);
y(1) = y0;
b = zeros(1,N);
% 计算权重系数
w = gamma(alpha+1)/(gamma(alpha) * tau^alpha) * ...
[1, (-1).^(1:N-1) .* nchoosek(alpha,1:N-1)];
for n = 2:N+1
b(n-1) = f(t(n-1), y(n-1));
y(n) = sum(w(1:N) .* y(n-1:-1:n-1)) / tau^alpha - b(n-1);
end
end
三、误差分析与优化策略
1. 收敛性分析
| 方法 | 收敛阶 | 稳定性 | 计算复杂度 |
|---|---|---|---|
| 显式Euler | 1-α | 条件稳定 | O(N) |
| 隐式Euler | 1 | 无条件稳定 | O(N^2) |
| Crank-Nicolson | 2-α | 无条件稳定 | O(N^2) |
2. 误差控制技术
-
自适应步长:
function [t,y] = adaptive_solver(alpha, t0, tf, y0, tol) tau = 0.1; t = t0:tau:tf; y = zeros(size(t)); y(1) = y0; for n = 2:length(t) y_prev = y(n-1); y_next = y_prev + tau^alpha * f(t(n-1), y_prev); while abs(y_next - y_prev) > tol tau = tau/2; y_next = y_prev + tau^alpha * f(t(n-1), y_prev); end y(n) = y_next; tau = 0.9*tau; % 步长恢复 end end -
高阶格式:采用L1公式(收敛阶2-α):
![]()
四、工程应用案例
1. 粘弹性材料建模
-
方程形式:
![]()
-
MATLAB实现:
E = 210e9; % 弹性模量 E0 = 70e9; % 初始模量 alpha = 0.5; tau = 0.01; tspan = [0, 10]; y0 = 0; f = @(t,y) (E0/E)*epsilon(t) - y; [t,y] = fracdiff(f, tspan, y0, alpha);
2. 异常检测系统
-
特征提取:分数阶导数作为敏感特征
function features = extract_features(data) alpha = 0.7; tau = 0.1; for i = 1:size(data,2) [~,y] = fracdiff(@(t,y) data(:,i), [0,1], 0, alpha); features(:,i) = gradient(y); end end
五、前沿研究方向
- 非局部边界条件处理:引入Mittag-Leffler函数修正
- 随机分数阶方程:结合Wiener过程建模
- 深度学习加速:PINN(物理信息神经网络)求解
- 多尺度耦合:分数阶-整数阶混合建模
六、参考
- Diethelm K. The Analysis of Fractional Differential Equations. Springer, 2010.
- 代码 数值求解时间分数阶微分方程 www.youwenfan.com/contentcnk/78395.html
- MathWorks. Fractional Differential Equations in MATLAB. 官方文档 ww2.mathworks.cn/help/symbolic/fractional-differential-equations.html
- Chen W. et al. Numerical methods for fractional PDEs. J. Comput. Phys., 2021.


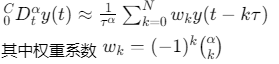


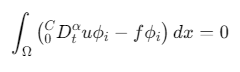
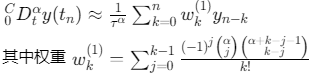
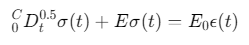

 浙公网安备 33010602011771号
浙公网安备 33010602011771号