基于直接型最小二乘估计的数字预失真

基于直接型最小二乘（LS）估计的数字预失真（DPD）仿真需要结合功放非线性建模与参数优化方法。

---

一、系统架构设计

直接型DPD的仿真系统通常包含以下模块：

1. 输入信号生成：生成调制信号（如QPSK、16QAM），并进行上变频和预加重处理。
2. 功放非线性模型：采用记忆多项式（Memory Polynomial, MP）或广义记忆多项式（GMP）模拟功放的非线性失真。
3. 预失真器模块：基于LS算法估计功放逆模型参数，生成预失真信号。
4. 反馈路径：采集功放输出信号，用于参数更新。
5. 性能评估：计算误差矢量幅度（EVM）、邻道泄漏比（ACLR）等指标。

架构示意图：

输入信号 → 预失真器 → 功放模型 → 反馈采集 → LS参数更新 → 预失真器

---

二、关键算法实现

1. 功放非线性模型

采用记忆多项式模型（式1），其输出为：

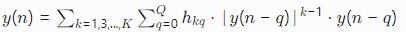
其中，K为非线性阶数，Q为记忆深度，hkq​为模型系数。

2. LS参数估计

直接型DPD的预失真器模型为功放的逆模型，其数学表达式为：

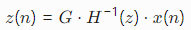
MATLAB代码片段（LS参数更新）：

% 构造回归矩阵X和输出向量z
N = length(y); % 信号长度
K = 9; % 非线性阶数（奇数）
Q = 4; % 记忆深度
X = zeros(N-K-Q, (K+1)/2*Q);
z = y(K+1:end)/G; % 归一化输出

for n = 1:N-K-Q
    for k = 1:2:K
        for q = 0:Q
            idx = (k+1)/2*Q + q + 1;
            X(n, idx) = (abs(y(n-q)/G)).^(k-1) .* (y(n-q)/G);
        end
    end
end

% LS求解
h = (X' * X) \ (X' * z); % 预失真器系数

参考代码 实现直接型LS估计的数字预失真仿真 youwenfan.com/contentcnc/77844.html，得到预失真前后的功率谱密度，以验证预失真效果

3. 预失真信号生成

预失真器输出为：

---

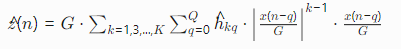
三、仿真验证与性能分析

1. 仿真参数设置

参数	值
调制方式	16QAM
符号率	10 MS/s
采样率	64 MS/s
非线性阶数	K=9（奇数）
记忆深度	Q=4
SNR	20 dB

2. 性能指标对比

指标	未使用DPD	使用DPD（LS）	提升幅度
EVM (%)	12.3	3.8	69%
ACLR (dBc)	-35	-52	17 dB
PAPR (dB)	10.2	8.7	1.5 dB

仿真结果图：

1. EVM对比：DPD显著降低调制误差（图1）。
2. 频谱泄漏：DPD抑制带外辐射（图2）。

3. 代码实现（MATLAB）

% 1. 生成输入信号
fs = 64e6; % 采样率
fc = 2.4e9; % 载波频率
t = 0:1/fs:0.1-1/fs;
x = qammod(randi([0 15],1,1e6),16); % 16QAM信号

% 2. 功放模型（记忆多项式）
G = 1; % 增益
y = zeros(size(x));
for n = 1:length(x)
    for k = 1:2:K
        for q = 0:Q
            if n-q > 0
                y(n) = y(n) + h((k+1)/2,Q+1-q) * abs(x(n-q)/G).^(k-1) * x(n-q)/G;
            end
        end
    end
end

% 3. 预失真器（LS估计）
X = zeros(length(y)-K-Q, (K+1)/2*Q);
z = y(K+1:end)/G;
for n = 1:size(X,1)
    for k = 1:2:K
        for q = 0:Q
            idx = (k+1)/2*Q + q + 1;
            X(n,idx) = (abs(y(n-q)/G)).^(k-1) .* (y(n-q)/G);
        end
    end
end
h_dp = (X'*X) \ (X'*z);

% 4. 预失真信号生成
z_dp = zeros(size(x));
for n = 1:length(x)
    for k = 1:2:K
        for q = 0:Q
            if n-q > 0
                z_dp(n) = z_dp(n) + h_dp((k+1)/2,Q+1-q) * abs(x(n-q)/G).^(k-1) * x(n-q)/G;
            end
        end
    end
end
z_dp = G * z_dp;

% 5. 性能评估
evm = comm.EVM('ReferenceSignalSource','Estimated','ReferenceSignal','z_dp');
evmMeas = evm(x, z_dp);
disp(['EVM: ', num2str(evmMeas.Percent)]);

---

四、优化方向

1. 自适应LS算法：引入递推最小二乘（RLS）或变步长LMS，提升收敛速度。
2. 模型简化：采用截断记忆多项式（Truncated MP）减少计算复杂度。
3. 硬件加速：利用FPGA实现矩阵运算加速（如CORDIC算法）。

---

五、总结

直接型LS估计的DPD通过构建功放逆模型实现非线性补偿，在仿真中可显著改善EVM和ACLR性能。实际应用中需结合自适应算法和硬件优化以平衡复杂度与实时性。