遗传算法进行自抗扰控制器参数整定

如求下列函数的最大值

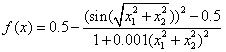
或者求：

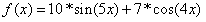
具体算法如下所示：

一、初始化(编码)
initpop.m函数的功能是实现群体的初始化，popsize表示群体的大小，chromlength表示染色体的长度(二值数的长度)，
长度大小取决于变量的二进制编码的长度(在本例中取10位)。

%Name: initpop.m
%初始化
function pop=initpop(popsize,chromlength)   
pop=round(rand(popsize,chromlength));      
% rand随机产生每个单元为 {0,1} 行数为popsize，列数为chromlength的矩阵，
% roud对矩阵的每个单元进行圆整。这样产生的初始种群。

二、计算目标函数值

1、将二进制数转化为十进制数(1)

%Name: decodebinary.m
%产生 [2^n 2^(n-1) ... 1] 的行向量，然后求和，将二进制转化为十进制
function pop2=decodebinary(pop)
[px,py]=size(pop);              %求pop行和例数
for i=1:py
    pop1(:,i)=2.^(py-1).*pop(:,i);
    py=py-1;
end
pop2=sum(pop1,2);              %求pop1的每行之和

2、将二进制编码转化为十进制数(2)
decodechrom.m函数的功能是将染色体(或二进制编码)转换为十进制，参数spoint表示待解码的二进制串的起始位置。(对于多个变量而言，如有两个变量，采用20为表示，每个变量10位，则第一个变量从1开始，另一个变量从11开始。本例为1)，参数1ength表示所截取的长度（本例为10）。

%Name: decodechrom.m
%将二进制编码转换成十进制
function pop2=decodechrom(pop,spoint,length)
pop1=pop(:,spoint:spoint+length-1);
pop2=decodebinary(pop1);

3、计算目标函数值
calobjvalue.m函数的功能是实现目标函数的计算，其公式采用本文示例仿真，可根据不同优化问题予以修改。

%Name: calobjvalue.m
%实现目标函数的计算
function [objvalue]=calobjvalue(pop)
temp1=decodechrom(pop,1,10);  %将pop每行转化成十进制数
x=temp1*10/1023;          %将二值域 中的数转化为变量域 的数
objvalue=10*sin(5*x)+7*cos(4*x);%计算目标函数值

三、计算个体的适应值

%Name:calfitvalue.m
%计算个体的适应值
function fitvalue=calfitvalue(objvalue)
global Cmin;
Cmin=0;
[px,py]=size(objvalue);
for i=1:px
    if objvalue(i)+Cmin>0

​      temp=Cmin+objvalue(i);
​    else

​      temp=0.0;
​    end
​    fitvalue(i)=temp;
end
fitvalue=fitvalue';

四 选择复制
选择或复制操作是决定哪些个体可以进入下一代。程序中采用赌轮盘选择法选择，这种方法较易实现。
根据方程 pi=fi/∑fi=fi/fsum ，选择步骤：
1）在第 t 代，由（1）式计算 fsum 和 pi
2）产生 {0,1} 的随机数 rand( .)，求 s=rand( .)*fsum
3）求 ∑fi≥s 中最小的 k ，则第 k 个个体被选中
4）进行 N 次2）、3）操作，得到 N 个个体，成为第 t=t+1 代种群

%Name: selection.m
%选择复制
function [newpop]=selection(pop,fitvalue)
totalfit=sum(fitvalue);%求适应值之和
fitvalue=fitvalue/totalfit;%单个个体被选择的概率
fitvalue=cumsum(fitvalue); %累积概率，如 fitvalue=[1 2 3 4]，则 cumsum(fitvalue)=[1 3 6 10] 
[px,py]=size(pop);
ms=sort(rand(px,1)); %从小到大排列，将"rand(px,1)"产生的一列随机数变成轮盘赌形式的表示方法，由小到大排列
fitin=1; %fivalue是一向量，fitin代表向量中元素位，即fitvalue(fitin)代表第fitin个个体的单个个体被选择的概率
newin=1; %同理
while newin<=px
 if(ms(newin))<fitvalue(fitin)      %ms(newin)表示的是ms列向量中第"newin"位数值，同理fitvalue(fitin)
newpop(newin,:)=pop(fitin,:);    %赋值 ,即将旧种群中 的第fitin个个体保留到下一代(newpop)
newin=newin+1;
 else
  fitin=fitin+1;
 end
end

五 2.5 交叉

交叉(crossover)，群体中的每个个体之间都以一定的概率 pc 交叉，即两个个体从各自字符串的某一位置
（一般是随机确定）开始互相交换，这类似生物进化过程中的基因分裂与重组。例如，假设2个父代个体x1，x2为：
x1=0100110
x2=1010001
从每个个体的第3位开始交叉，交又后得到2个新的子代个体y1，y2分别为：
y1＝0100001
y2＝1010110
这样2个子代个体就分别具有了2个父代个体的某些特征。利用交又我们有可能由父代个体在子代组合成具有更高适合度的个体。
事实上交又是遗传算法区别于其它传统优化方法的主要特点之一。

%Name: crossover.m
%交叉
function [newpop]=crossover_multiv(pop,pc)
global Numv 
[px,py]=size(pop);
m=py/Numv;
for j=1:Numv
  pop1=ones(px,m);
  pop2=pop(:,m*(j-1)+1:m*j);    %取出相应变量对应的二进制编码段 
  for i=1:2:px-1
    if(rand<pc)
      cpoint=round(rand*(m-1));  %cpoint为交叉点
      pop1(i,:)=[pop2(i,1:cpoint) pop2(i+1,cpoint+1:m)];
      pop1(i+1,:)=[pop2(i+1,1:cpoint) pop2(i,cpoint+1:m)];
    else
      pop1(i,:)=pop2(i,1:m);
      pop1(i+1,:)=pop2(i+1,1:m);
    end
  end
  newpop(:,m*(j-1)+1:m*j)=pop1;          %将交叉后的一个参数的编码放入新种群中
end

六、变异
变异(mutation)，基因的突变普遍存在于生物的进化过程中。变异是指父代中的每个个体的每一位都以概率 pm翻转，即由“1”变为“0”，或由“0”变为“1”。遗传算法的变异特性可以使求解过程随机地搜索到解可能存在的整个空间，因此可以在一定程度上求得全局最优解。

%Name: mutation.m
%变异
function [newpop]=mutation(pop,pm)
[px,py]=size(pop);
newpop=ones(size(pop));
for i=1:px
  if(rand<pm)
     mpoint=round(rand*py);
     if mpoint<=0
        mpoint=1;
     end
     newpop(i,:)=pop(i,:);
     if any(newpop(i,mpoint))==0
        newpop(i,mpoint)=1;
     else
        newpop(i,mpoint)=0;
     end
  else
     newpop(i,:)=pop(i,:);
  end
end

七、求出群体中最大得适应值及其个体

%Name: best.m
%求出群体中适应值最大的值
function [bestindividual,bestfit]=best(pop,fitvalue)
[px,py]=size(pop);
bestindividual=pop(1,:);
bestfit=fitvalue(1);
for i=2:px
    if fitvalue(i)>bestfit
      bestindividual=pop(i,:);
      bestfit=fitvalue(i);
    end
end

八、主程序

%Name:genmain05.m
clear
clf
popsize=20;                          %群体大小
chromlength=10;                       %字符串长度（个体长度）
pc=0.6;                            %交叉概率
pm=0.001;                           %变异概率
pop=initpop(popsize,chromlength);           %随机产生初始群体
for i=1:20                          %20为迭代次数
[objvalue]=calobjvalue(pop);              %计算目标函数
fitvalue=calfitvalue(objvalue);            %计算群体中每个个体的适应度
[newpop]=selection(pop,fitvalue);           %复制
[newpop]=crossover(pop,pc);               %交叉
[newpop]=mutation(pop,pc);                %变异
[bestindividual,bestfit]=best(pop,fitvalue);%求出群体中适应值最大的个体及其适应值
y(i)=max(bestfit);
n(i)=i;
pop5=bestindividual;
x(i)=decodechrom(pop5,1,chromlength)*10/1023;
pop=newpop;
end
fplot('10*sin(5*x)+7*cos(4*x)',[0 10])
hold on
plot(x,y,'r*')
hold off

完整代码 adrc 参数整定 对于控制器的复杂参数整定进行算法优化