弹性波有限差分数值模拟生成波场快照（交错网格）

1. 弹性波方程与交错网格

在弹性波数值模拟中，通常使用一阶速度-应力方程来描述波的传播。对于二维各向同性介质，弹性波方程可以表示为：

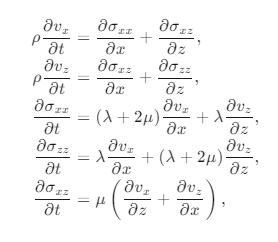
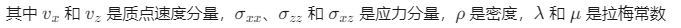
交错网格技术通过将不同物理量布置在不同网格点上，可以有效减少数值频散。具体来说：

2. 有限差分格式

为了数值求解上述方程，通常采用有限差分方法。时间导数通常采用二阶中心差分，空间导数则可以采用高阶有限差分格式以提高精度。例如，空间导数可以使用 ( 2N ) 阶有限差分格式。

3. 波场快照生成

波场快照是通过在特定时间步记录波场的状态来生成的。以下是生成波场快照的基本步骤：

1. 初始化模型参数：包括速度、密度、弹性参数等。

2. 应用震源函数：在模型中指定震源位置并施加震源信号。

3. 时间步进循环：

   • 更新速度分量。

   • 应用边界条件。

   • 更新应力分量。

   • 应用边界条件。

4. 记录波场快照：在适当的时间步记录波场的状态。

4. MATLAB实现

简单的MATLAB代码，用于生成弹性波场快照：

% 参数设置
dx = 10; % 空间步长 (m)
dz = 10; % 空间步长 (m)
dt = 0.001; % 时间步长 (s)
nx = 100; % x方向网格数
nz = 100; % z方向网格数
nt = 500; % 时间步数
​
% 初始化速度和应力场
vx = zeros(nx, nz);
vz = zeros(nx, nz);
sxx = zeros(nx, nz);
szz = zeros(nx, nz);
sxz = zeros(nx, nz);
​
% 震源参数
source_x = 50; % 震源x位置
source_z = 50; % 震源z位置
f0 = 10; % 震源频率 (Hz)
t0 = 1 / f0; % 震源起始时间
source = zeros(nt, 1);
for it = 1:nt
    t = (it-1) * dt;
    source(it) = -2 * (t - t0) * exp(-((t - t0) / (0.6 / f0))^2);
end
​
% 时间步进循环
for it = 1:nt
    % 更新速度分量
    for ix = 2:nx-1
        for iz = 2:nz-1
            vx(ix, iz) = vx(ix, iz) + dt / rho * (sxx(ix, iz) - sxx(ix-1, iz) + sxz(ix, iz) - sxz(ix, iz-1)) / dx;
            vz(ix, iz) = vz(ix, iz) + dt / rho * (sxz(ix, iz) - sxz(ix-1, iz) + szz(ix, iz) - szz(ix, iz-1)) / dz;
        end
    end
    
    % 应用震源
    vx(source_x, source_z) = vx(source_x, source_z) + source(it);
    
    % 更新应力分量
    for ix = 2:nx-1
        for iz = 2:nz-1
            sxx(ix, iz) = sxx(ix, iz) + dt * lambda * (vx(ix, iz) - vx(ix-1, iz)) / dx + dt * mu * (vx(ix, iz) - vx(ix-1, iz)) / dx;
            szz(ix, iz) = szz(ix, iz) + dt * lambda * (vz(ix, iz) - vz(ix, iz-1)) / dz + dt * mu * (vz(ix, iz) - vz(ix, iz-1)) / dz;
            sxz(ix, iz) = sxz(ix, iz) + dt * mu * ((vx(ix, iz) - vx(ix, iz-1)) / dz + (vz(ix, iz) - vz(ix-1, iz)) / dx);
        end
    end
    
    % 记录波场快照
    if mod(it, 10) == 0
        figure;
        imagesc(vx);
        title(['波场快照，时间步 = ', num2str(it)]);
        colorbar;
        pause(0.1);
    end
end

5. 性能优化

为了提高数值模拟的效率，可以采用并行计算技术。例如，基于GPU的并行计算可以显著减少计算时间。

6. 应用案例

该方法已被成功应用于多种场景，例如地震波场模拟和复杂介质中的波场分析。

参考代码 弹性波有限差分数值模拟生成波场快照交错网格