泛洪算法（Flood fill Algorithm）:符号洪水填充算法

泛洪算法（Flood fill Algorithm）:符号洪水填充算法

算法别名：

　　漫水填充算法、种子填充算法（Seed Fill）

作用：

 　　用于确定连接到多维数组中给定节点的区域，可以用来标记或者分离图像的一部分，实现如Ps中自动选区功能。

基本思想：

 　　顾名思义就像洪水漫过一样，把一块连通的区域填满。

　　当然水要能漫过需要满足一定的条件，可以理解为满足条件的地方就是低洼的地方，水才能流过去。

　　在图像处理中就是给定一个种子点作为起始点，向附近相邻的像素点扩散，把颜色相同或者相近的所有点都找出来，并填充上新的颜色，这些点形成一个连通的区域。

 

算法参数：

1. 起始节点（start node）
2. 目标颜色（target color）
3. 替换颜色（replacement color）

算法实现：

漫水填充算法实现最常见有四邻域像素填充法，八邻域像素填充法，基于扫描线的填充方法。根据代码实现方式又可以分为递归与非递归。

 

1、四邻域递归实现

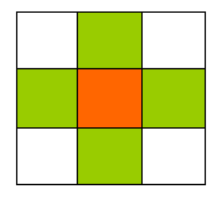
 将像素点(x,y)周围的上下左右四个点分别进行着色。

//Recursive 4-way floodfill, crashes if recursion stack is full
public void floodFill4(int x, int y, int newColor, int oldColor)  
{  
    if(x >= 0 && x < width && y >= 0 && y < height   
         && getPixel(x, y) == oldColor && getPixel(x, y) != newColor)   
    {   
        setPixel(x, y, newColor); //set color before starting recursion  
        floodFill4(x + 1, y, newColor, oldColor);  
        floodFill4(x - 1, y, newColor, oldColor);  
        floodFill4(x, y + 1, newColor, oldColor);  
        floodFill4(x, y - 1, newColor, oldColor);  
    }     
}

　　

2、八邻域递归实现

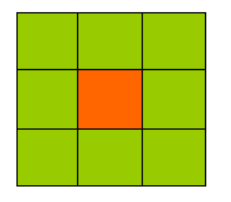
 将一个像素点的上下左右，左上，左下，右上，右下都进行着色。

public void floodFill8(int x, int y, int newColor, int oldColor)  
{  
    if(x >= 0 && x < width && y >= 0 && y < height &&   
            getPixel(x, y) == oldColor && getPixel(x, y) != newColor)   
    {   
        setPixel(x, y, newColor); //set color before starting recursion  
        floodFill8(x + 1, y, newColor, oldColor);  
        floodFill8(x - 1, y, newColor, oldColor);  
        floodFill8(x, y + 1, newColor, oldColor);  
        floodFill8(x, y - 1, newColor, oldColor);  
        floodFill8(x + 1, y + 1, newColor, oldColor);  
        floodFill8(x - 1, y - 1, newColor, oldColor);  
        floodFill8(x - 1, y + 1, newColor, oldColor);  
        floodFill8(x + 1, y - 1, newColor, oldColor);  
    }     
} 

3、扫描线算法(Scanline Fill)：

　　利用填充线来加速算法， 它不是在堆栈上推动每个潜在的未来像素坐标，而是检查相邻线（前一个和下一个）以找到可能在未来通过中填充的相邻段， 线段的坐标（开始或结束）被推到堆栈上。 在大多数情况下，该扫描线算法至少比每像素算法快一个数量级。 

　　该算法的过程是：先扫描一行或者一列内的连通像素，然后再上下行或者左右列扫描，可以减少递归栈的深度。

 

 递归方式：递归实现算法好理解，但当连通的区域很大时，很可能会导致栈溢出。

void floodFillScanline(int x, int y, int newColor, int oldColor){
    if(newColor==oldColor) return;
    if(screen[x][y]!=oldColor) return;
    int x1=x;
    while(x1<w&&screen[x1][y]==oldColor){
        screen[x1][y]=newColor;
        x1++;
    }
    x1=x-1;
    while(x1>=0&&screen[x1][y]==oldColor){
        screen[x1][y]=newColor;
        x1--;
    }
    x1=x;
    while(x1<w&&screen[x1][y]==newColor){
        if(y<h-1&&screen[x1][y+1]==oldColor) floodFillScanline(x1,y+1,newColor,oldColor);
        x1++;
    }
    x1=x-1;
    while(x1>0&&screen[x1][y]==newColor){
        if(y>0&&screen[x1][y+1]==oldColor) floodFillScanline(x1,y+1,newColor,oldColor);
        x1--;
    }
    x1=x;
    while(x1<w&&screen[x1][y]==newColor){
        if(y<h-1&&screen[x1][y-1]==oldColor) floodFillScanline(x1,y+1,newColor,oldColor);
        x1++;
    }
    x1=x-1;
    while(x1>0&&screen[x1][y]==newColor){
        if(y>0&&screen[x1][y-1]==oldColor) floodFillScanline(x1,y+1,newColor,oldColor);
        x1--;
    }
}

非递归方式：

void floodFillScanline(int x, int y, int newColor, int oldColor){
    if(newColor==oldColor) return;
    if(screen[x][y]!=oldColor) return;
    emptyStack();
    int x1;
    bool spanAbove, spanBelow;
    if(!push(x,y)) return;
    while(pop(x,y)){
        x1=x;
        while(x1>0&&screen[x1][y]==oldColor) x1--;
        x1++;
        spanAbove = spanBelow = 0;
        while(x1<w&&screen[x1][y]==oldColor){
            screen[x1][y]=newColor;
            if(!spanAbove&&y>0&&screen[x1][y-1]==oldColor){ //这里判断出了上行的元素可以被染色，可能为了修改screen的访存连续性，所以这里没修改。而且你改了上行的值，却没考虑其四周，会有完备性的问题。
                if(!push(x1,y-1)) return;
                spanAbove=1;
            }
            else if(spanAbove&&y>0&&screen[x1][y-1]!=oldColor){
                spanAbove=0; //不压入重复过多的元素
            }
            if(!spanBelow&&y<h-1&&screen[x1][y+1]==oldColor){
                if(!push(x1,y+1)) return;
                spanBelow=1;
            }
            else if(spanBelow&&y<h-1&&screen[x1][y+1]!=oldColor){
                spanBelow=0;
            }
            x1++;
        }
    }
}

 

 

 

 

 

 

 

参考：https://blog.csdn.net/Eason_Y/article/details/127782837