概率论重要题目
重要的题目
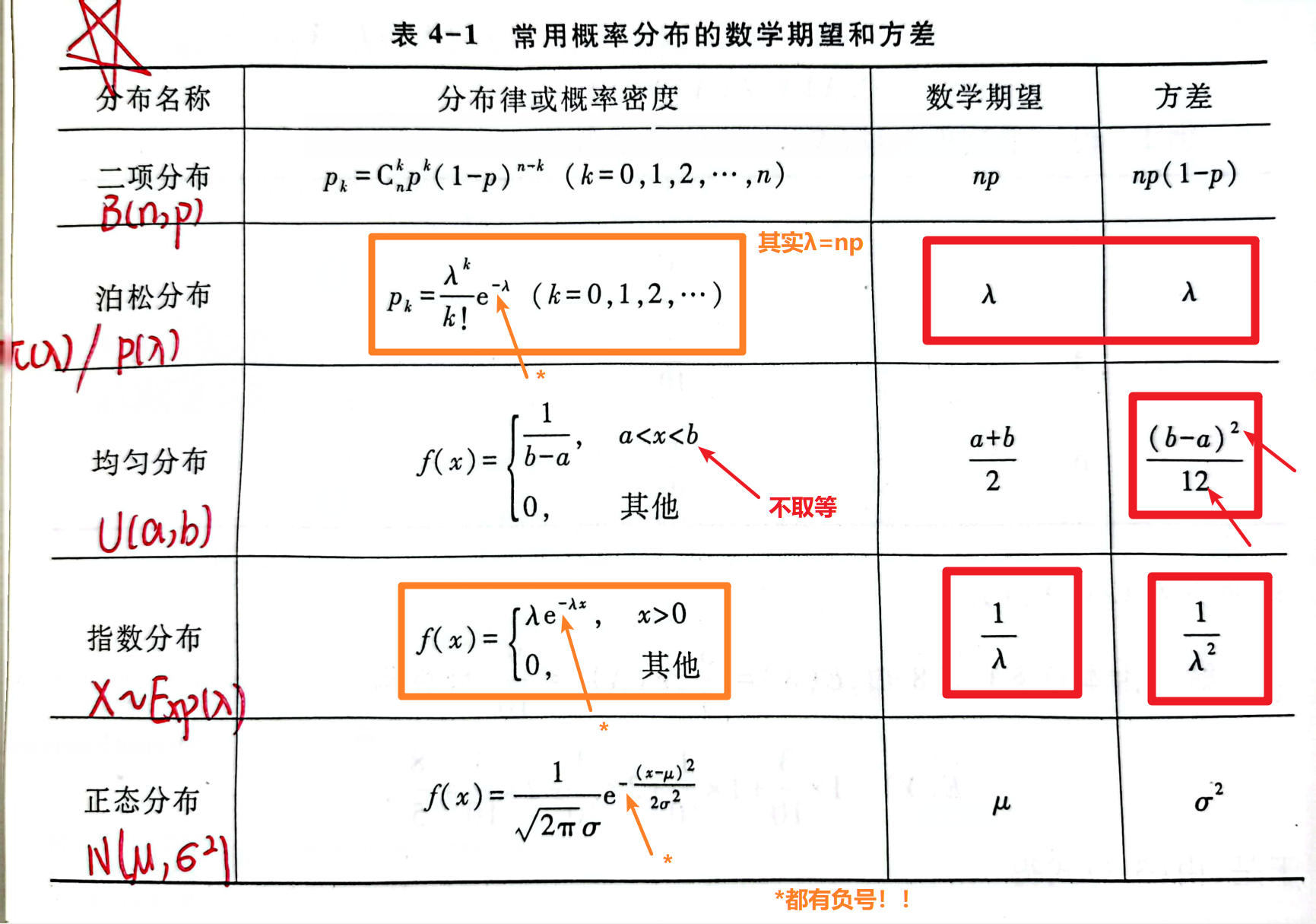
全概率公式和贝叶斯公式的难题
例一
例二
例三
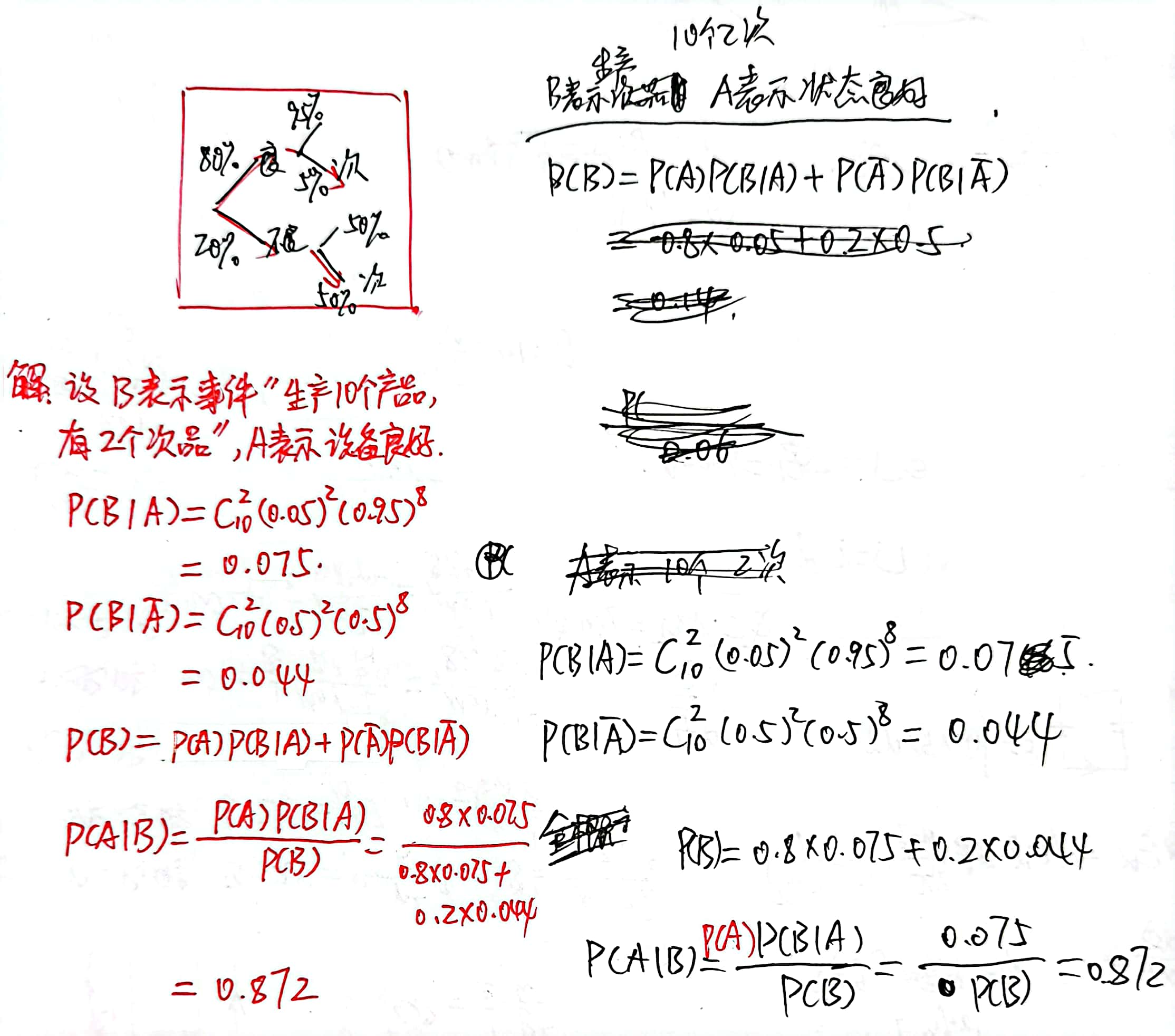
随机变量函数的分布
套娃函数
还有这个
数学期望的利润最大问题
记得随机变量的期望公式：∫xf(x)dx
随机变量函数的期望公式：∫g(x)f(x)dx
二维随机变量函数的期望公式：∫∫g(x, y)f(x, y)dxdy
掷骰子的最大点数的分布
落在子区间的概率与区间长度成正比
二维随机变量
二维离散型随机变量
二维随机变量函数的分布
1、中规中矩地二重积分
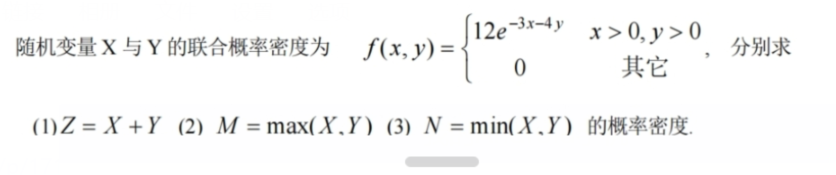
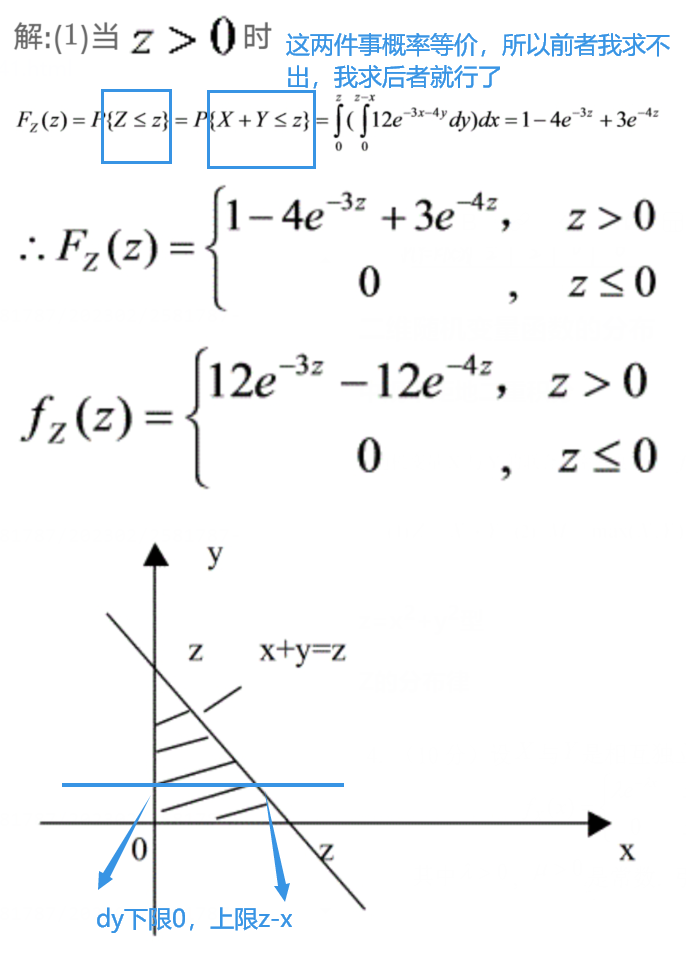
2、z=x2+y2型
书上没有，略
记住∫ρdρ就行了
3、Z的分布律
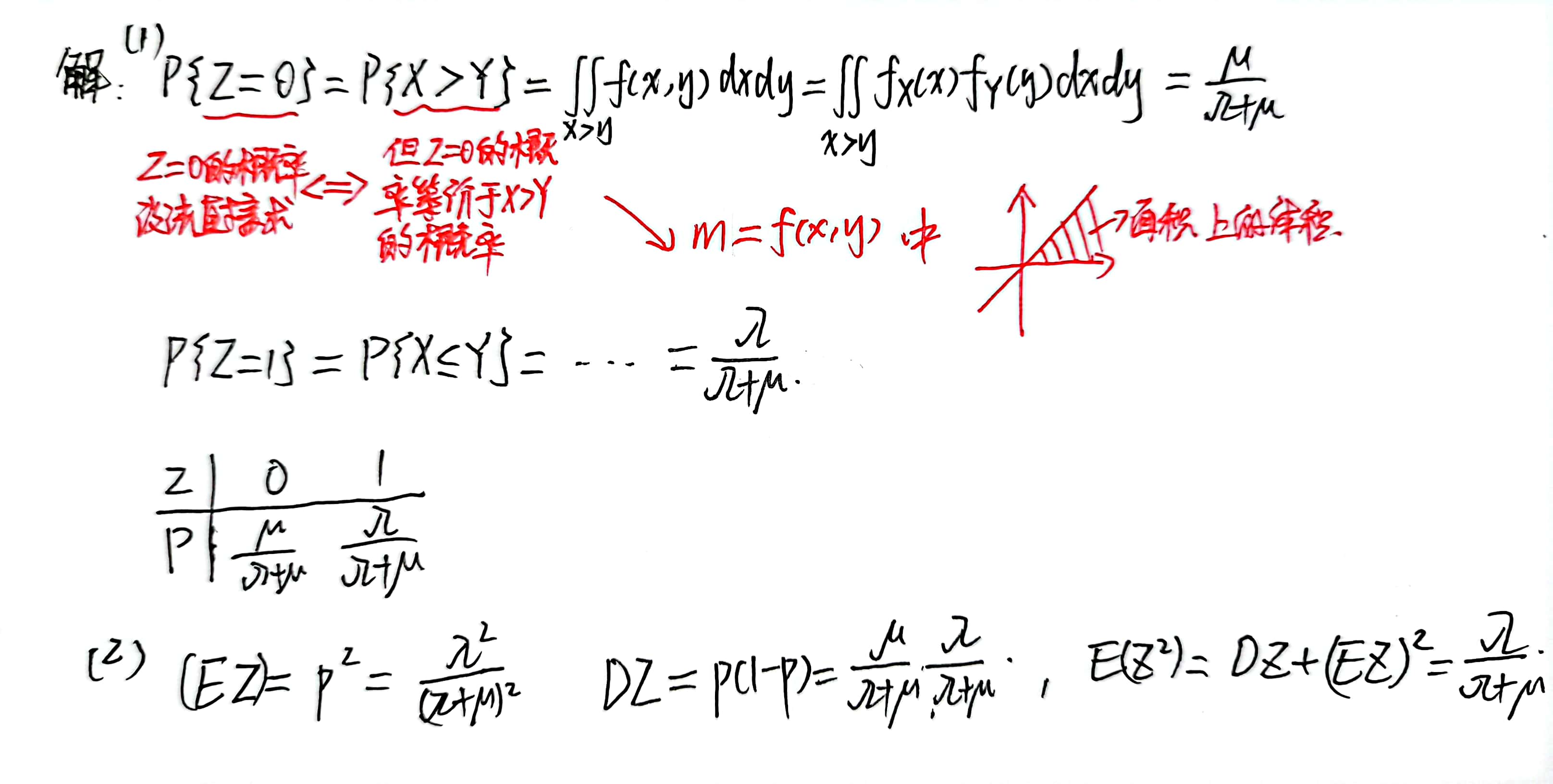
4、z=max(x, y)和z=min(x, y)
这里由于只知道x和y的联合分布，不知道他们分别的分布函数，所以不能用max的分布函数的那个公式，但那个公式就是用这种方法推出来的
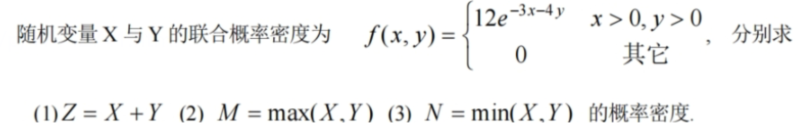
5、z=|x-y|型
常规
如果X, Y都是正态分布
6、二维离散型随机变量的函数的分布
别忘了二项分布/01分布都是离散的，因此要求的是分布律
还有这题，是试卷上的
样本均值的期望（非常重要）
样本均值的期望等于总体的均值，总体的均值不一定是μ，要根据具体的分布自己算，总体的方差也是。样本标准差的期望等于总体方差
矩估计和极大似然估计
1、极大似然函数有两个变元（正态分布）就求偏导
2、θ要尽可能地大，但是要包住所有样本，所以取样本的最小值
3、由最大似然估计的不变原则知...
若g(θ)具有单值反函数，则g(θ)的最大似然估计为g(θ^)
估计的无偏性
假设检验
第一类错误：弃真，P{拒绝H0 | H0为真}，具体来讲就是直接用H0的数据，然后算拒绝H0的概率就行了
第二类错误：取伪，P{接受H0 | H0为假}
