量子编程
量子计算机编程(一)——QPU编程
今天要给大家介绍的是这本书《Programming Quantum Computers —— Essential Algorithms and Code Samples》,主要讲如何在量子计算机上编程,又示例的代码可以跑 https://oreilly-qc.github.io./ ,这本书的理解方向是纯粹计算机的,连矩阵都很少涉及,一个量子计算机就像是协处理器一样,很像我们现在的GPU。
这本书一共分为三个部分,我也将分成三篇文章来写。
单量子比特
这本书中对于量子的表达方式如下circle notation:


蓝色圈的面积就是这个量子态测量后是这个状态的概率,中间的蓝色短线代表他们的相位,因为全局相位也观察不出来,所以一般|0⟩|0⟩就是朝上的。对于一个量子比特来说,重要的也就这两个,magnitude和relative phase(可能因为重要的是概率大小,所以他其实没有提amplitude其实是一个复数)。
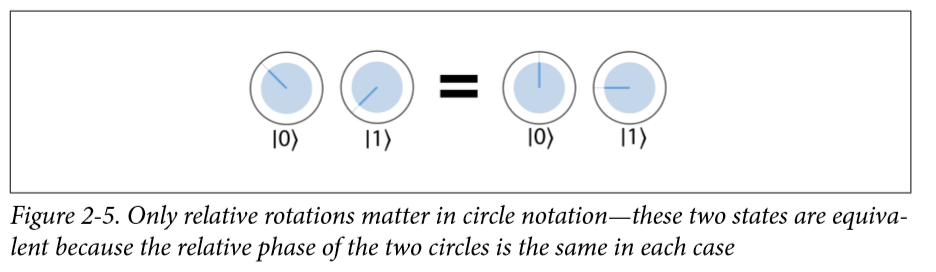
这两个态实际上是等价的。
电路图呢,一般长这样
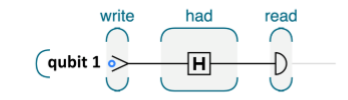
这个电路图对应的代码如下:(这个例子都可以在上面那个网站上跑起来)
qc.reset(1); // allocate one qubit
qc.write(0); // write the value zero
qc.had(); // place it into superposition of 0 and 1
var result = qc.read(); // read the result as a digital bit
第一步就是申请一个qubit,就像你要给变量分配空间一样。
第二步写0,其实写0很容易,你可以直接测量,要么0,要么1,如果结果是1的话,再做一个not操作就好;当然,你要是嫌麻烦,对于一个qubit,长时间的静置他,他也会变成0,毕竟还是基态比较稳定。
第三步就是进行一个H门的操作
第四步读,其实就是测量了
常见的作用于单量子比特操作的表达方式:


其中值得一提的是PHASE相位操作,phase操作只作用在 |1⟩|1⟩ 上,因为他的效果是改变相对相位,如果大家都改变就没有什么用了。可能有同学听说过绕X轴旋转和绕Y轴旋转,这些都是针对Bloch球的表达方式,与这里的circle notation的方式不要弄混了。
一个操作也可能是其他几个操作的组合,比如:
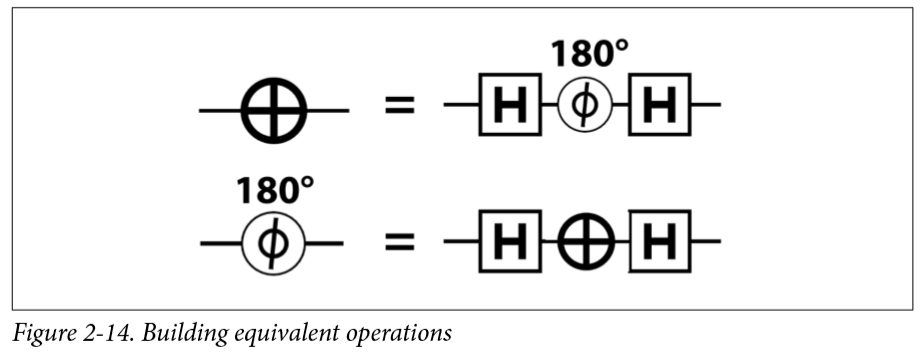
如果我们可以把not变成H+180°旋转+H,那么我们也可以把中间的180°旋转变成两个90°的旋转,中间再加上两个H,因为HH=IHH=I,他们可以相互抵消,这样我们还可以得到RNOT:

COPY:这是一个需要注意的操作,因为量子程序里没有复制,这也保障了量子传输的信息不会被窃听, 因为你要窃听,你就需要去读,一读就是测量,而量子比特一测量就是坍缩。由于量子不能复制,所以,上述所有操作都是在原有的那个比特上操作的,所以操作就会被发现。
一个简单例子:
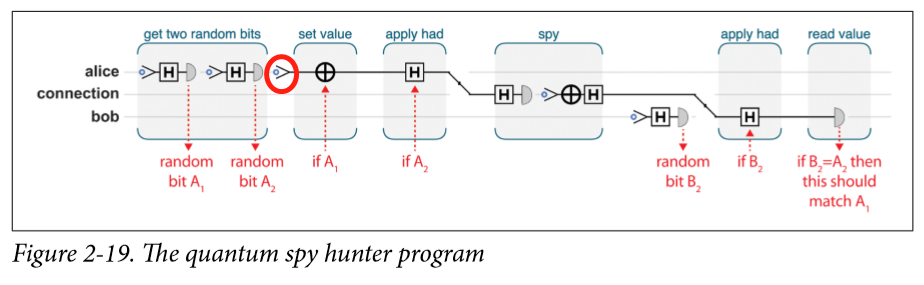
对于这里例子来说, A1A1 和 A2A2 是对qubit Hadmard门操作后测量得到的随机值,因为这个是真随机,所以就不会被窃听者提前知道或者预估,那么当我传输这个被我用红色圈出来的比特的时候,spy并不知道这个比特是否执行了H门和not操作,那他就只能猜了,25%的概率,图里面所示就是他猜有执行了,然后他再按照他的猜测如法炮制一个qubit继续传递,当B收了这个bit后,B也随机一个数据B2B2,看是否执行H门,然后测量。这个时候消息也都收到了,测量也都测量好了,那么把 A2A2的信息发过来也和窃听没有关系了,如果 B2B2 A2A2 的结果一样,那么测量结果应该一样,如果不一样,那么一定被窃听了。
这样的成功概率有多少呢? B2B2 A2A2 一样的概率0.5,在这种情况下spy被发现的概率0.25。看起来不是很高,但是如果我们有一百个比特先检测一下这条线路,不被发现的概率将会降到百万分之一。
现在来看一下代码:https://oreilly-qc.github.io/?p=2-4
qc.reset(3);//申请三个qubit
qc.discard();
var a = qint.new(1, 'alice'); //给其中一个变量命名为a,但是画出来的电路图中显示alice
var fiber = qint.new(1, 'fiber');
var b = qint.new(1, 'bob');
function random_bit(q) {//对一个初始化为0的比特,进行H操作,然后测量,测量结果是随机的
q.write(0);
q.had();
return q.read();
}
// Generate two random bits
qc.label('get two random bits');
var send_had = random_bit(a);//得到是否执行H门的随机值
var send_value = random_bit(a);//得到是否not的随机值
qc.label('');
// Prepare Alice's qubit
a.write(0);//a重新赋值为0,所以前面取随机值的操作也可以在a上进行
qc.label('set value');
qc.nop();
if (send_value)
a.not();
qc.nop();
qc.label('');
qc.nop();
qc.label('apply had');
qc.nop();
if (send_had)
a.had();
qc.nop();
qc.label('');
// Send the qubit!
fiber.exchange(a);
// Activate the spy
var spy_is_present = true;
if (spy_is_present)
{
var spy_had = 1;
qc.nop();
qc.label('spy');
if (spy_had)
fiber.had();
stolen_data = fiber.read();
fiber.write(0);
if (stolen_data)
fiber.not();
if (spy_had)
fiber.had();
qc.label('');
qc.nop();
}
// Receive the qubit!
var recv_had = random_bit(b);
fiber.exchange(b);
qc.label('apply had');
qc.nop();
if (recv_had)
b.had();
qc.nop();
qc.label('');
qc.nop();
qc.label('read value');
qc.nop();
recv_val = b.read();
qc.nop();
qc.label('');
qc.nop();
// Now Alice emails Bob to tell
// him her had setting and value.
// If the had setting matches and the
// value does not, there's a spy!
if (send_had == recv_had)
if (send_value != recv_val)
qc.print('Caught a spy!\n');
多量子比特
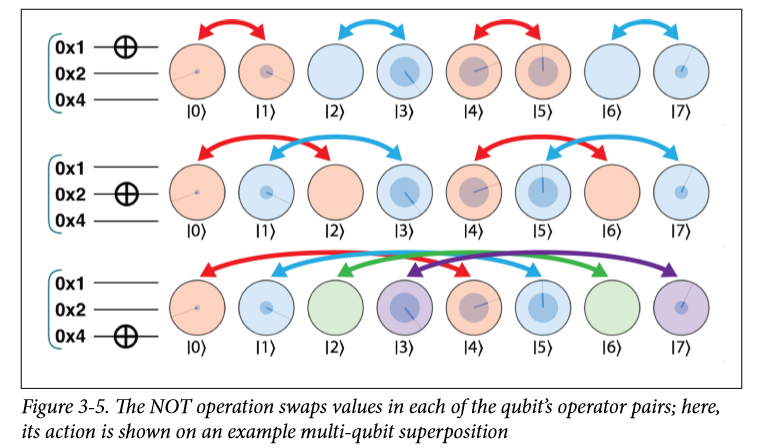
多量子比特的表示方法和单量子比特没有什么区别,下面的数字就是把他们从01的二进制换算成了我们熟悉的十进制。0x是十六进制的表示方法,最上面的是地位,正好可以not操作表示了出来,0就是000,1就是001,2就是010……以此类推
真要说和单量子比特的区别,那主要是两方面,一个是纠缠;另一个就是受控操作。
纠缠
纠缠好说,两个纠缠的量子比特就是其中一个的测量结果会影响另一个。
具体可以看一下这篇量子纠缠1——量子比特、Bell态、EPR佯谬
受控操作
受控操作就是说有两类比特,一个是用来控制的,另一个是被控制的。
比如大家耳熟能详的CNOT,当控制比特是1的时候,就翻转被控制的比特,如果控制比特是0的时候,那就不做操作。还有CCNOT门,又叫做toffli门,有两个控制比特,只有当他们都为1的时候才翻转。
现在要介绍一个前面没有提过的CPHASE受控相位门,和CNOT相似,同样是当控制比特为1的时候才进行,但是正如前面我们提过,PHASE操作只操作在1上,也就是说,如果这个操作被执行其实只有一种情况,那就是|11⟩|11⟩ 。
在前面我们表示过一个旋转180°的相位操作可以表示成一个 H+NOT+H figure 2-14
那么现在受控相位操作拥有了三种表示方法: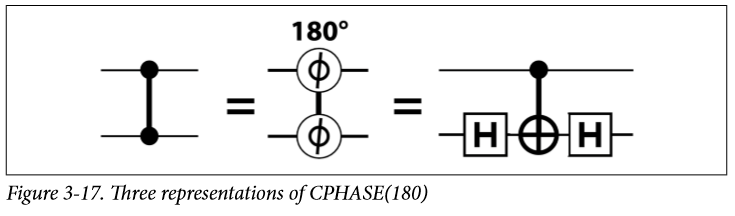
当控制比特为0的时候,CNOT就不会发生,两个H又正好抵消了。
phase kickback
在这之所以说这么多的受控相位操作是因为这里面有个一很有趣的小技巧 QPU Trick: Phase Kickback 来看下面这个电路图

这个电路图很容易理解,一种理解方式就是把register 1当作控制比特,register 2 当作受控比特,两个H门使得register 1变成了等可能的四种情况 12|00⟩+12|01⟩+12|10⟩+12|11⟩12|00⟩+12|01⟩+12|10⟩+12|11⟩ 。
现在来看看结果:

因为register 2并不是叠加态,所以没有相对相位,而绝对相位又测不出来,所以他可以说是没有变的,改变了的,反而是register 1 , |3⟩|3⟩ 转了135°是因为两个都为1,45°和90°都转了。作为一个受控操作,控制比特反而变了,而受控比特没有改变。
swap
受控操作当然也能连在一起,得到一些有用的结果,比如三个CNOT操作,他就可以交换两条线路。
这个的证明是一件很容易的事情,你可以取一个任意态推一边,专门把这个提出来说一遍是因为这个还能做一件有趣的事情,那就是验证两个比特是否相等。我们需要用到的是CSWAP,即当控制比特为1时才交换。
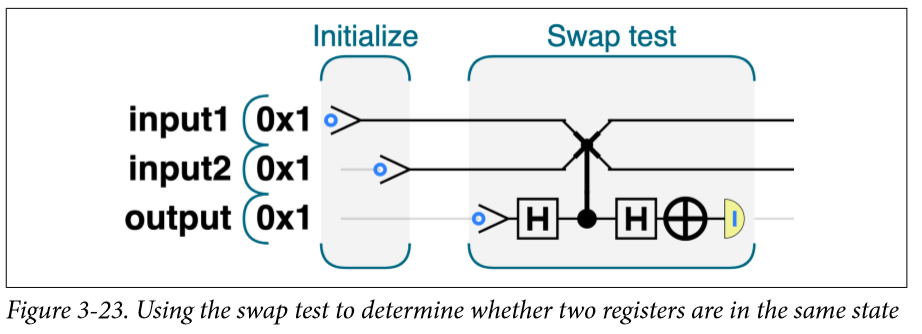
当我们的output比特经过H门后,他就变成了等概率的 |0⟩|0⟩ 和 |1⟩|1⟩ 经过一个CSWAP,为1情况下的input1和input2就会交换,也就是说他们原来x概率的ab就变成了x概率的ba了,这样的问题出在哪?
如果概率还是原来的分布,那么在经过一个H门output等待率的 |0⟩|0⟩ 和 |1⟩|1⟩ 又会化简成 |0⟩|0⟩ ,各种各样的 |1⟩|1⟩ 的概率会相互抵消掉,那么在经历一个NOT操作就一定会得到1。
那,如果这两个数据不一样,就一定得不到1吗?不一定,只是他有概率不是1,而一旦有概率不是1,那只要多检测几次就一定能检测出来,就像上面那个窃听一样,明明只有四分之一的概率,但仅需要一百次,测不出来的可能性就降到了百万分之一。
当然,代码在这里https://oreilly-qc.github.io/?p=3-4,这也是这本书的特色了。
受控操作当然不止这些,但是很多受控操作都可以分解成CNOT加上一些相位操作,我们可以自己构造自己需要的操作。
远距离操控随机
这里的远距离操控不是指我能扣确定他是什么,如果我能确定,那就不是随机了,而是说,我把两个比特弄成纠缠,当我一个测出来是0的时候,另一个以x%的概率得到0,至于我测出来是不是0看天意,对面测出来是不是0,也看天意,其中唯一能确定的,就只有这个x了。
这个例子是书上例子3-6 https://oreilly-qc.github.io/?p=3-6 方法很简单,就是我H门操作后,我旋转45°的角度,这样再来一个H门,因为相位变了,符号对不上,所以回不去了,就有了关联。
更强大的一点的应用是——量子隐形传态,量子隐形传态 Quantum Teleportation 提过了,就不在累述。
量子计算机编程(二)——QPU基础函数
第二部分主要是QPU的基础功能,第一部分就像是我们有了哪些基本的语句,第二部分就是我们能写一些简单基础的函数,一些小模块,第三部分就是他的应用了。
先来看一下一个简单量子应用的结构: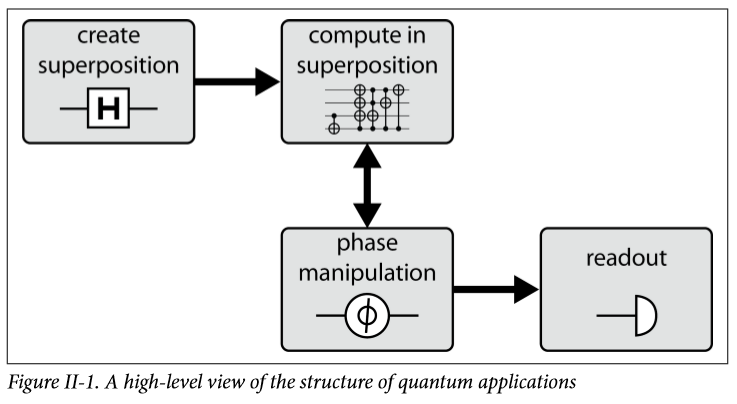
第一步,将量子态通过H门变成叠加态,很多应用的第一步都是H门,因为量子的叠加态正是她的优越性所在,所谓n个qubit可以表达 2n2n 种状态, 2n2n 种可能性同时并行,这是叠加态带来的好处,要是一直使用基态,经典的不香吗?还便宜,量子的还需要在靠近绝对零度的温度下进行。
第二步,在叠加态中运算。
第三步,相位操作,叠加态中运算的结果当然也是叠加态的,但我们要获取,只能获取经典的信息,直接读的话,那他就是随机坍缩,信息丢失,当然你要是打算重复多次也行,但是有的时候,我们想要的并不是这个态的全部信息,我们可能需要的仅仅是他的一些特征,可能是一个序列的周期,我并不需要这个序列具体是什么,如此的话,可能一些相位变化操作就可以直接读取你想要的信息,这样更为方便。所以量子算法的设计,不仅仅要考虑量子怎么加速,还要考虑量子加速完了的结果能不能读出来。
第四步,读取。
量子算数逻辑
在量子之前,我们有经典算数和经典的数字逻辑,那么量子和经典有什么区别呢:
- 没有copy ,量子的信息不能复制,如果我们要把一个信息传给另一个,我们只能swap交换一下,或者我们还可以teleportation,总之,我们只能交换,不能赋值,具体一点来说,以前我们写程序的里面的赋值“=”是没有的。
- 可逆,除了测量,QPU上的所有操作都是可逆的。
![]()
说到逻辑,我们已经还记得数字逻辑里面学的全加器吧,c=a+b之类的操作,这个简单的加法后面是一堆的与或非门的结构,量子的也同样如此,结构也都差不多,不同之处就两点: |a⟩|b⟩|a⟩|b⟩ 的进去 |a+b⟩|b⟩|a+b⟩|b⟩ 的出来,因为量子要求可逆,他不会把a、b变成c,一旦合成了c,那就分不出a、b了,当然,你也可以 |a⟩|b⟩|0⟩|a⟩|b⟩|0⟩ 的进去 |a⟩|b⟩|a+b⟩|a⟩|b⟩|a+b⟩,这样也是可以的;第二点就是叠加,这里的a、b不再是某个具体的数,而是一个叠加态。
如果是负数,那怎么表达呢?
和经典一样,我们可以负数的话,首位变成1。就像 000-0 001-1 002-2 003-3 100-(-4) 101-(-3) 110-(-2) 111-(-1),非常熟悉的配方的了。
关于条件判断呢,给大家看一个例子: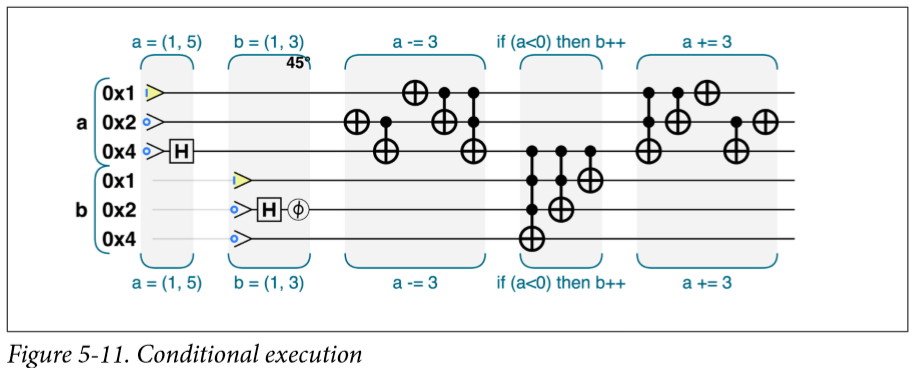
这是是如果a>3那么b就自增,如果没有,那就不用了,3不是很好的判断标准,但是0是啊,小于他的负数,直接首位编码就是1,所以,可以先-3,判断完了,增加好了,在把3加回来,办法总比问题多。
以上是量子和经典较为相似的部分,但是除此之外,量子还有新的特性,比如说:相位,接下来的篇幅都是属于他的。
振幅放大 Amplitude Amplification
我们先来说说振幅放大是什么:
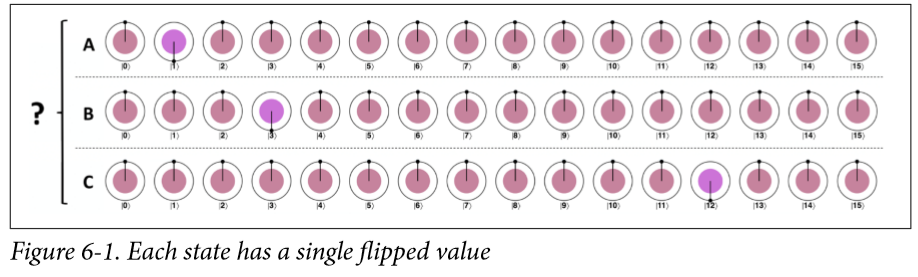

你觉得 Figure 6-1中的ABC三个qubit一样吗?不一样,直接看图很显然的不一样,虽然大家都是等概率的叠加态,但是他们相对相位180°的地方不一样。可是直接读,能读出来吗?即使我重复很多遍,但是他们的概率是一样的,no difference。但是,看图 Figure 6-3,就是可读的不一样了,振幅放大(AA)就是把他们从图6-1变成图6-3的方法。
现在我们已经只要了what和why了,接下来就是怎么进行how。
我们先来看一个单独的AA: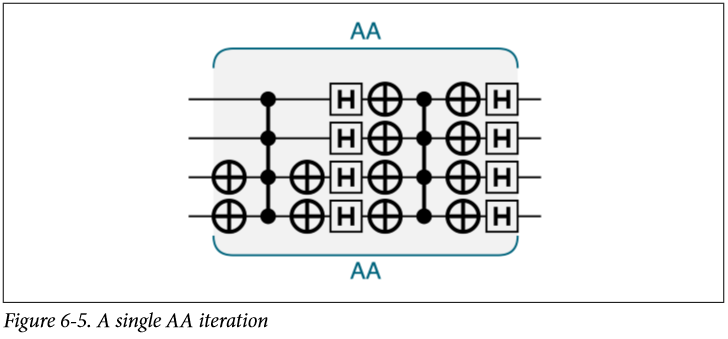
前面三步,也就是在4个H门之前是将这个叠加态中的某一个态给翻转他的相位,使他于其他态不同,接下来的几个步骤是把这个态的概率放大,至于问什么能放大,可以来看这篇 量子搜索算法 Grover search 这篇文章里主要是矩阵的角度,现在这个正好是一个具体的表现。
一次AA结束后,我们又回到了最初的相位,除了,我们翻转相位的那个态的振幅变大了,如果我们想要他继续变大,那么我们就继续AA,每一个AA都要包括将相位翻转的步骤。
你可能会疑惑,既然我们都知道要翻转哪一个态了,那为什么要费这么大的力气,这里,我们的翻转非常简单,就是找到这个态,然后翻转,上图就是两个not操作,但是在实际操作中,这可能是是一系列计算的结果。
AA一次就放大一些,再AA就再放大,那么是不是越多,就越能无线逼近1呢?
https://oreilly-qc.github.io/?p=6-2这是上面这个的实验,大家可以变换代码里面的 number_of_iterations,来验证一下刚刚的猜测,其实看图也能发现,B4B4的概率是小于B3B3的,why,事实上,这个概率大小是一个类似三角函数的存在: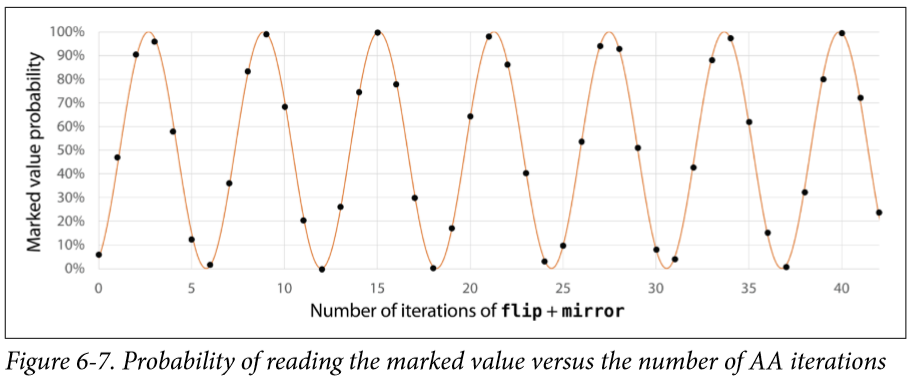
那么如何找到自己最合适的迭代次数呢?
书上给了一个未经过证明的公式Optimal number of iterations in amplitude amplification
这本书是一本是实践为主的书籍,他还考虑了另一个问题,如果在这个里面我不仅仅要翻转一个态,我要翻转的是两个、三个又会怎么样呢?
https://oreilly-qc.github.io/?p=6-3 同样给大家一个连接,大家可以改变n2f这个数组的大小,和每次的迭代次数,看一看结果会有什么变化,当然这么做有些麻烦,也可以看下面的图,分别是4个qubit的情况下翻转2、3、7、8个态的效果长什么样,这里我就直接公布答案,随着翻转的态越来越大,这我们的这个三角函数的周期会越来越小。


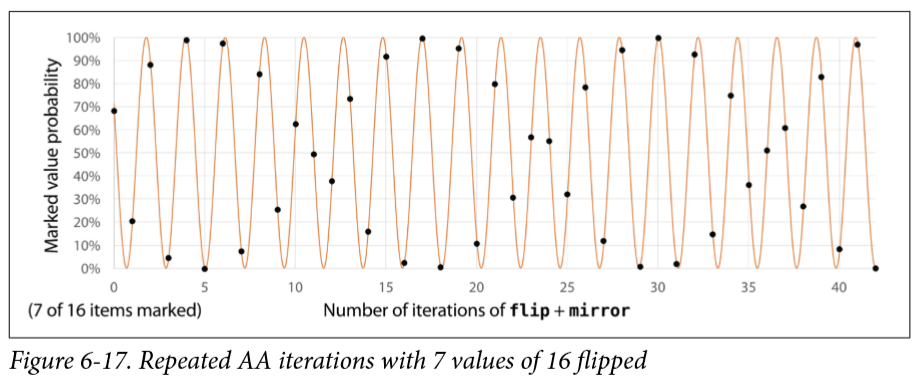

那么现在的最佳迭代次数又是多少呢?m是翻转的个数。
这里,我们再总结一下AA的意义,他把不可读的相位信息变成了可读的振幅信息。
量子傅里叶变换
提出一个技术,必定是为了解决一个问题,这里我们要解决的问题就是周期: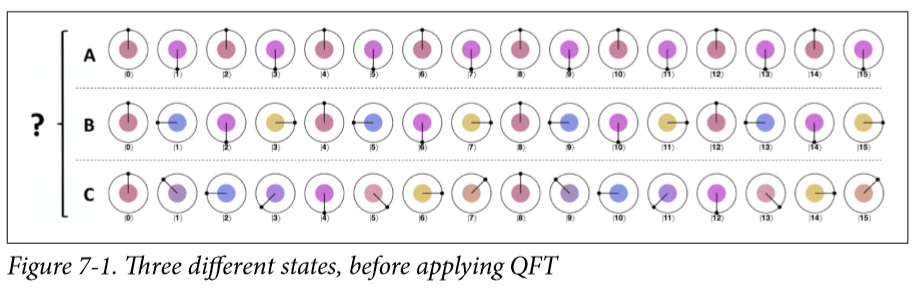
对于ABC这三个态,振幅放大也并不能很好的将他们区分,但是量子傅里叶变换(QFT)可以,他能够把上面这三个态变成下面这样:
A里面的有八个这样的周期,B里面有四个这样的周期,而C里面只有2个这样的周期,通过他们周期个数的不一样就可以轻而易举的把这三个态分辨出来。
量子傅里叶变换是一个封装好了的函数,直接调用.QFT就可以了。
var num_qubits = 4;
qc.reset(num_qubits);
var signal = qint.new(num_qubits, 'signal')
// prepare the signal制备量子态C
qc.label('prep');
signal.write(0);
signal.hadamard();
signal.phase(45, 1);
signal.phase(90, 2);
signal.phase(180, 4);
// Run the QFT直接调用
qc.label('QFT');
signal.QFT()
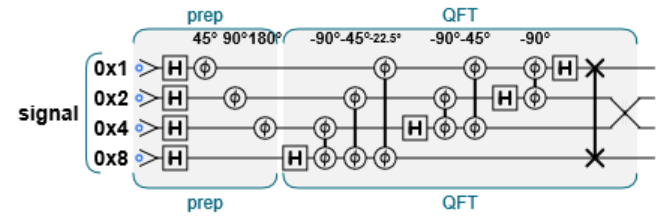
为什么这样就可以找到她的周期了呢?量子傅里叶变换
不过,QFT不是每次都能像现在这样获得这么好的结果的,像经典的傅里叶变换会有mirror-image,如下:

量子傅里叶也可能会有这种结果,我们同样也是取前面的一半:
选择量子傅里叶的好处在于,他很快,比快速傅里叶都还要快,他们的速度比值是这样的: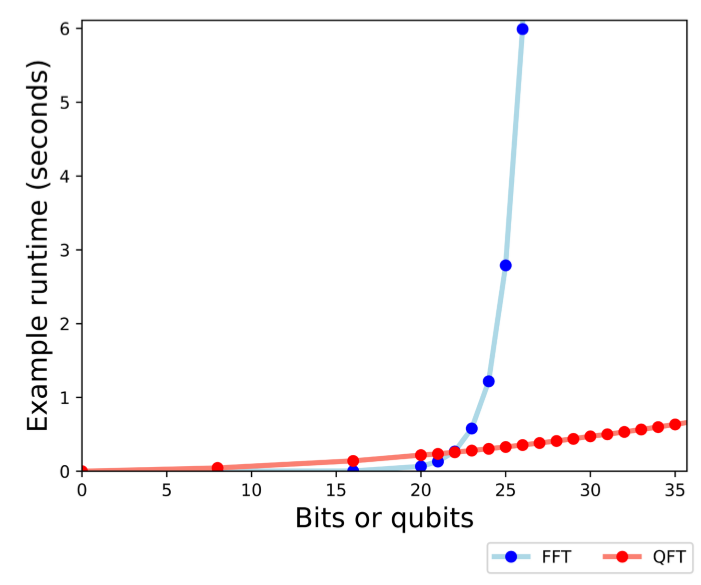
量子处理器的内部结构长这个样子: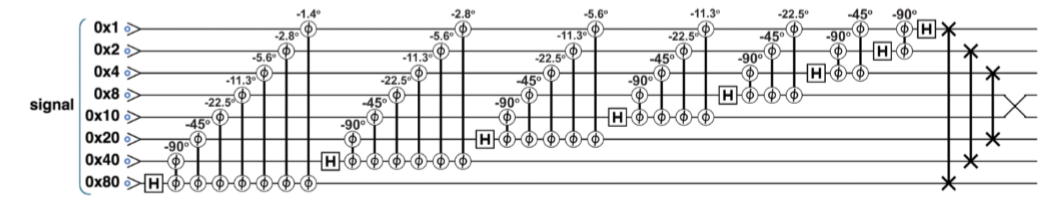
量子相位估计
这个关注的对象是量子操作的信息而不是量子寄存器的信息,每一个量子操作都可以用一个酉矩阵表示,而每一个量子态也可以用一个向量来表示,如果一个操作作用的量子态正好是他的特征向量会怎么样?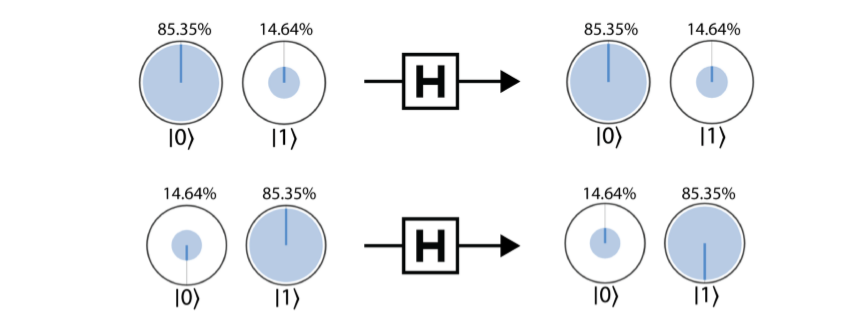
每一个操作都有自己的eigenstate和对应的eigenphase
所以相位估计究竟是做什么的呢?
假设我有一个操作U,以及操作的特征态u1,u2,u3,...u1,u2,u3,...,量子相位估计可以测出这些特征态所对应的特征相位。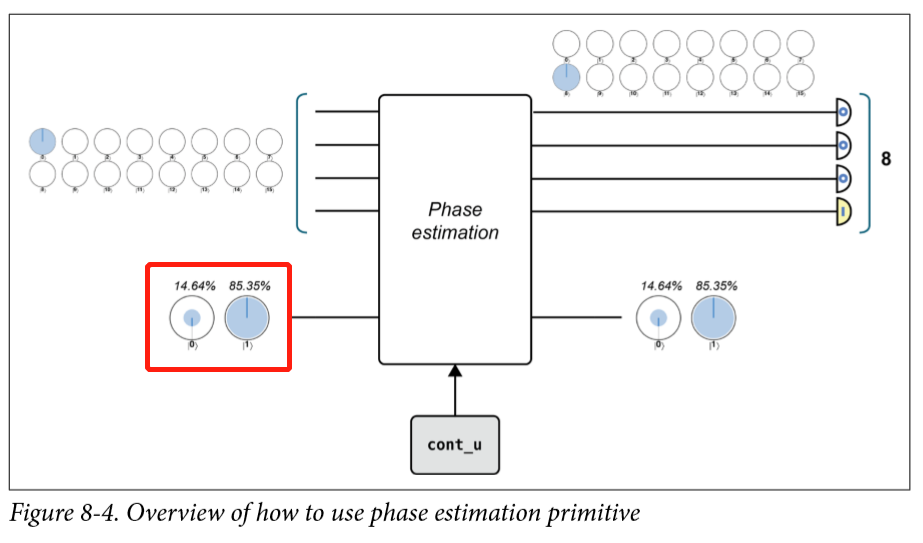
一个简单例子,cont_u是我们输入的操作,红框里,是这个操作的特征态,输出结果是8,这里有4个qubit,最大的输出结果可以是16,那么他对应的量子相位是:(8/16)*360°=180°,qubit的增加可以增加数据的精度,如果我们有最大误差要求,那么可以通过下面这个公式知道我们最小需要多少个量子比特:
调用这个函数非常简单:qin是特征向量,cout_u是操作,qout就是我们的结果,她的位数取决于我们需要的精度。
// Operate phase estimation primitive on registers phase_est(qin, qout, cont_u);
// Read output register
qout.read();
那么这个里面的操作又是长什么样子呢?
虽然看起来是上面在控制下面,但是仔细想一想 −|0⟩|1⟩−|0⟩|1⟩你能分清楚这个负号是0还是1的吗?,相位信息就这样在qout里累加,最后一个逆傅里叶变换得到我们的结果。
量子计算机编程(三)——量子应用
量子编程一层层搭建,最后是应用层
都到应用了,肯定会涉及数据,本节内容主要包括,量子数据、量子搜索、量子超级采样、Shor算法、量子机器学习。
真实数据
和数据有关的讨论一般围绕在两个方面,存储和表示。
QRAM
本书没有讨论QRAM如何制造,只是提了用法。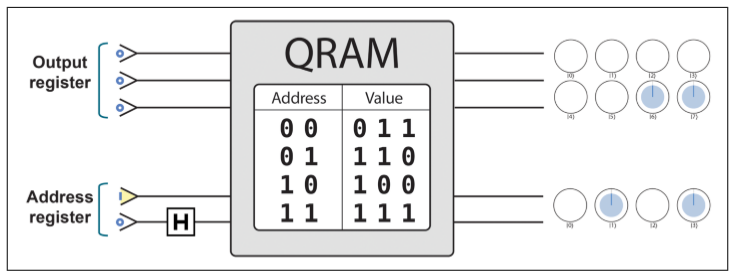
和普通的QRAM有一个重要区别,地址也可以是叠加态。
表示
小数:我们可以借鉴经典的手法,就像经典里面如何表达浮点数的一样,我们也这样来表述量子的小数,Qn.mQn.mn位的数据,其中m位是小数,(n-m)位是整数。
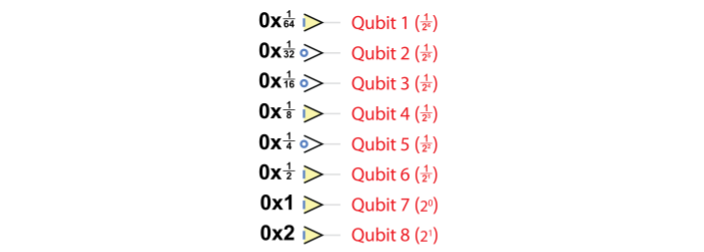
向量: [0,1,2,3]这个向量要怎么表示?
最基础的: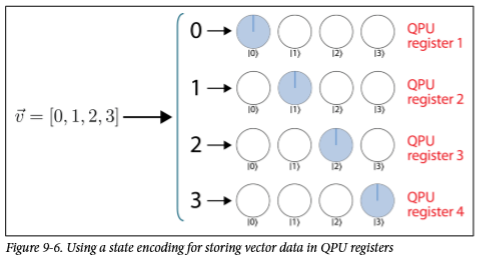
很容易理解,但是也很浪费空间,没有用到量子自身的特性。
amplitude encoding for vectors: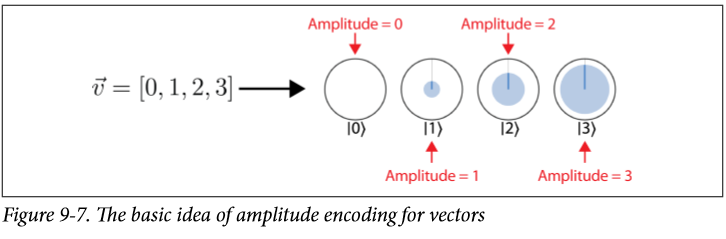
这个就利用了量子的性质,不过他也有自己的局限性:
- 量子叠加态基本就是 unREADable 的
- 因为概率需要归一化,所以他能表示的态也需要归一化
矩阵:
整体思路是用opertate来表示矩阵:
不过这里有两个限制:operator只能unitary的,矩阵不仅不一定是unitary,都不一定是hermitian的。解决方案如下:
不是hermitian的矩阵,可以构建成hermitian,通过 H=[0X†X0]H=[0XX†0]
- Deconstruct H=H1+…HnH=H1+…Hn 把H分解成更容易模拟的hermitian(也就是更容易执行第二步)
- Simulate components U=exp(−iHt)U=exp(−iHt) 操作只有unitary的操作,但是矩阵可以把他们联系到一起
- Reconstruction 把得到的U乘起来,因为H是在指数上分解的,所以这里直接乘起来就可以
量子搜索Quantum Search (QS)
Phase Logic ,我们不仅可以改变他们的0或者1,还可以通过01来改变量子态的相位,就像这样:

相位逻辑和其他逻辑最大的区别就是他把操作结果隐藏到了unreadable的相位里,通过改变叠加态里的相位,我们可以在一组寄存器里标记很多的态,并且还能通过AA之类的方法提取出来。
输入值还是那些量子态,输出值则被编码到了相对相位里。
那么这些是怎么完成的呢?简单的相位逻辑的组件: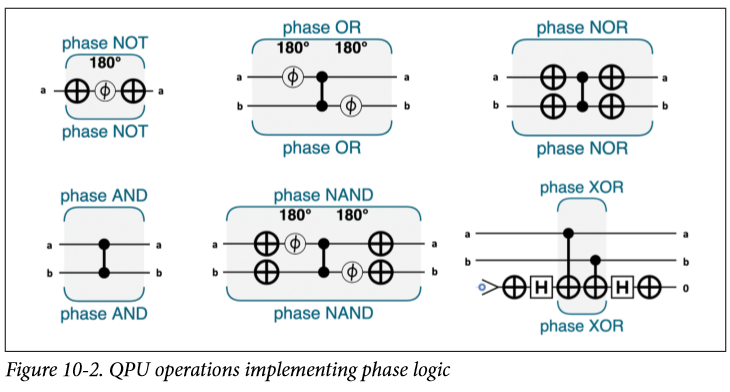
所以这个有什么用?
围观一个小公主找国王爸爸要礼物的例子:
小公主想要一只小猫咪,爸爸就给了他两个盒子,盒子A说:至少有一个盒子有猫咪,盒子B说:另一只盒子有老虎。
爸爸又说,这两个盒子要么同时为真,要么同时为假。
于是我们的小公主殿下搞出了这么一个数字逻辑:
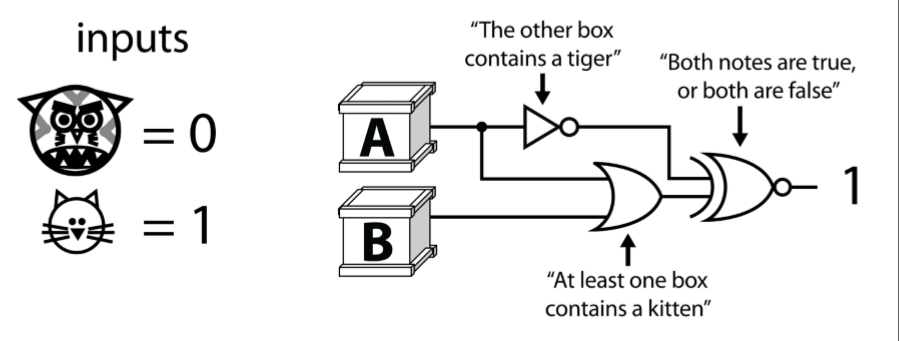
这样,跑把四种可能性都跑一遍,输出为1就满足了逻辑。
但是爸比就是很喜欢为难他的小可爱,他给公主提出一个要求,这个装置只能跑一次。
于是小公主就搞了一个量子版本:
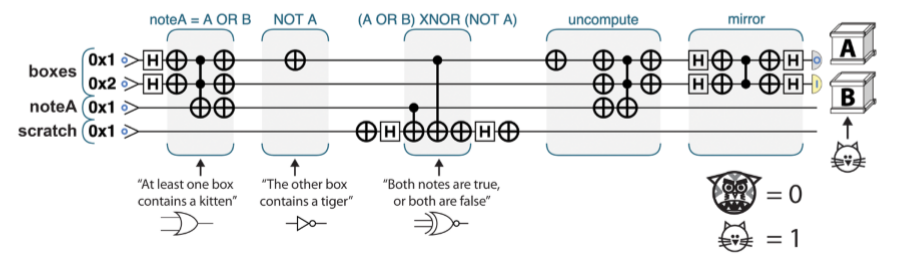
首先,用量子的把实验跑一遍,相对相位上把答案翻转,然后做实验的逆操作(所有的量子操作都是可逆的),现在答案就写在|00⟩,|01⟩|10⟩|11⟩|00⟩,|01⟩|10⟩|11⟩的相对相位里,再grover把他们找到。
实验在这里,https://oreilly-qc.github.io/?p=10-2
把答案翻转后的状态:
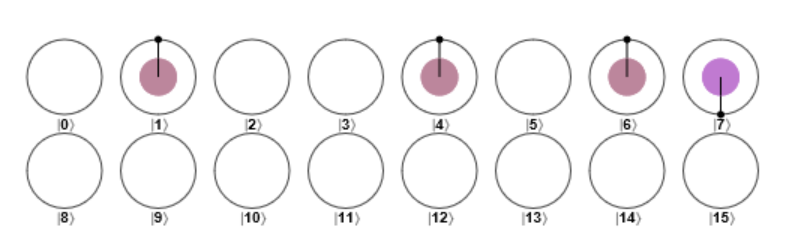
把答案 uncompute后:
Grover mirror 后: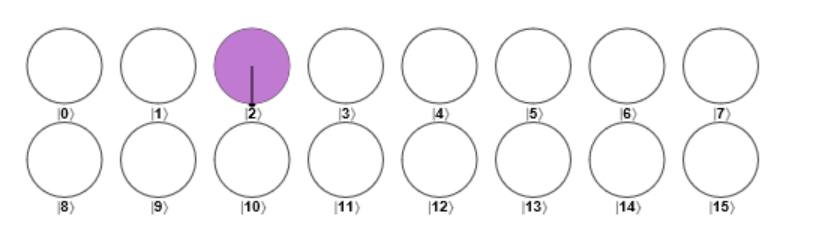
量子超采样
超采样是什么?
简单的说,这是抗锯齿的一种方法,电脑显示的图片由像素组成,一条线如果不是完全水平或者竖直,那么表现出来就会有锯齿,超采样就是在像素内部的多个实例处(而不是像正常情况一样在中心处)获取颜色样本,然后计算平均颜色值。通过以比显示的图像高得多的分辨率渲染图像,然后使用多余的像素进行计算将其缩小到所需的大小,以此达到目的。
这项任务,我们执行并行处理(计算与场景交互的许多光线的结果),但最终仅需要结果的总和,而不是单个结果本身。(听起来就可以量子加速)
那么量子处理器在这里能做些什么吗?

不过首先,在应用QSS之前,我们要知道如何用量子寄存器来表示图像。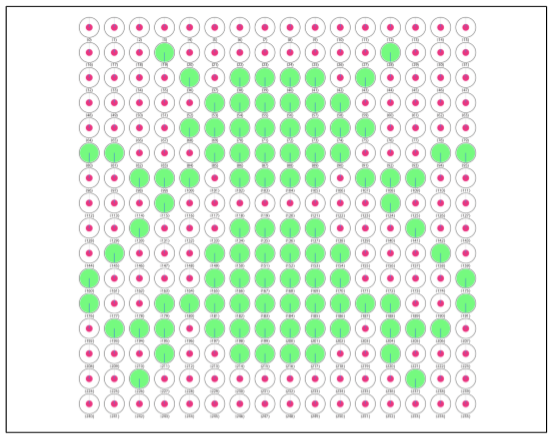
这样就拥有一张画布,我们可以通过相位翻转来改变他们的颜色,我们在上面施加的操作就是画笔。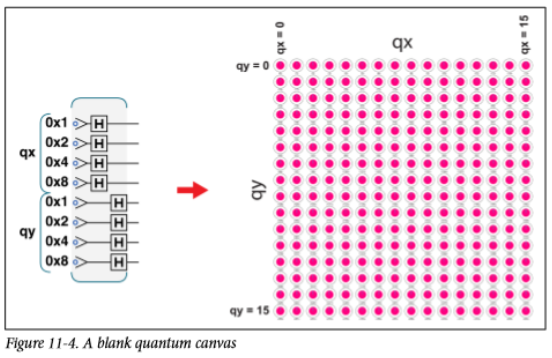
如果想要画曲线怎么办:https://oreilly-qc.github.io/?p=11-2 这是一个画了曲线的例子。
现在我们来讨论超级采样,对于每个图块,我们要估计已被相位翻转的子像素的数量。在黑白子像素(为我们表示为翻转或非翻转相位)的情况下,这使我们能够为每个最终像素获取一个代表其原始组成子像素强度的值。
此问题与前面“多个翻转项”中的“量子和估计”问题完全相同。要使用量子和估计,我们仅将实现绘制指令的量子程序视为用于翻转子程序的幅度放大量子程序。将其与第7章中的量子傅立叶变换相结合,可以近似估算每个图块中翻转的子像素的总数。
不过这样得到值不是确定的翻转的数目,我们需要将这个值和look up table结合着来看。
如果还在考虑颜色问题,那就是RGB各来一张图就好。
Shor算法
因数分解究竟在做什么,大家可以看一眼这个 因数分解算法、周期查找算法(简化)
默认大家看完有了大概了解,现在来看一个具体例子:因数分解15=3*5
代码是简单的调用
var N = 15; // The number we're factoring
var precision_bits = 4; // See the text for a description of this
var coprime = 2; // For this QPU implementation, this must be 2
var result = Shor(N, precision_bits, coprime);
整个过程一共有八步,•Steps 1–4制备 axmod(N)axmod(N) 的叠加态,Steps 5–6 量子傅里叶找到周期 Steps 7–8 拿到周期后计算因数
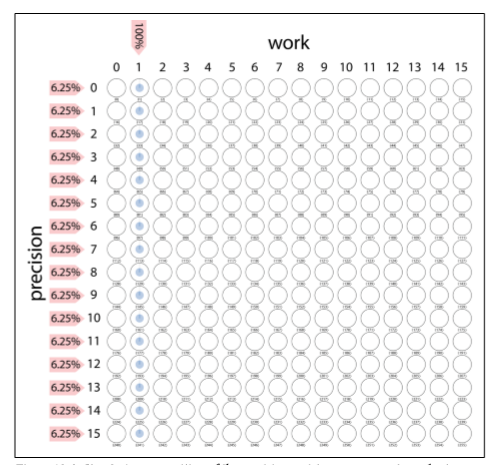
- Step 1: Initialize QPU Registers
- Step 2: Expand into Quantum Superposition

前面两个步骤结束后就是红色箭头这里,现在量子态的状态如下:
- Step 3: Conditional Multiply-by-2
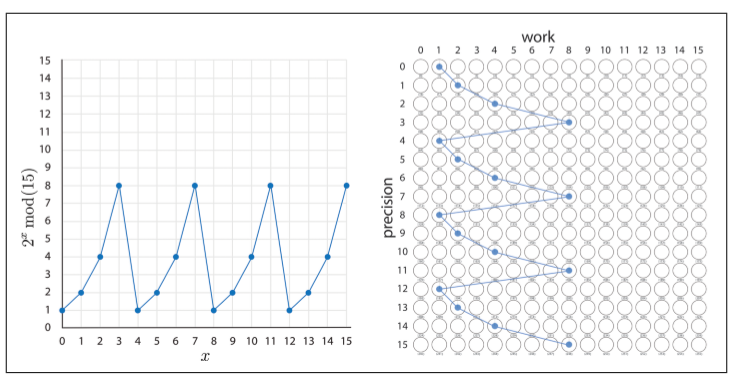
这一步是用来计算2x2x,任何的二进制寄存器都可通过简单的移位实现2的乘积(或者实际上是2的任何幂)。在我们的例子中,每个量子位都与下一个最高加权位置交换。需要注意的是我们将只使用精度寄存器的两个最低权重的量子位来表示x的值(这意味着x可以取值0、1、2、3),线路为图上iter0
- Step 4: Conditional Multipy-by-4
线路为图上iter1,目前我们已经得到了axax,对于我们考虑过的特定示例,我们的电路设法自动处理模数。
乘2和乘4后量子态的状态如下:

- Step 5: Quantum Fourier Transform
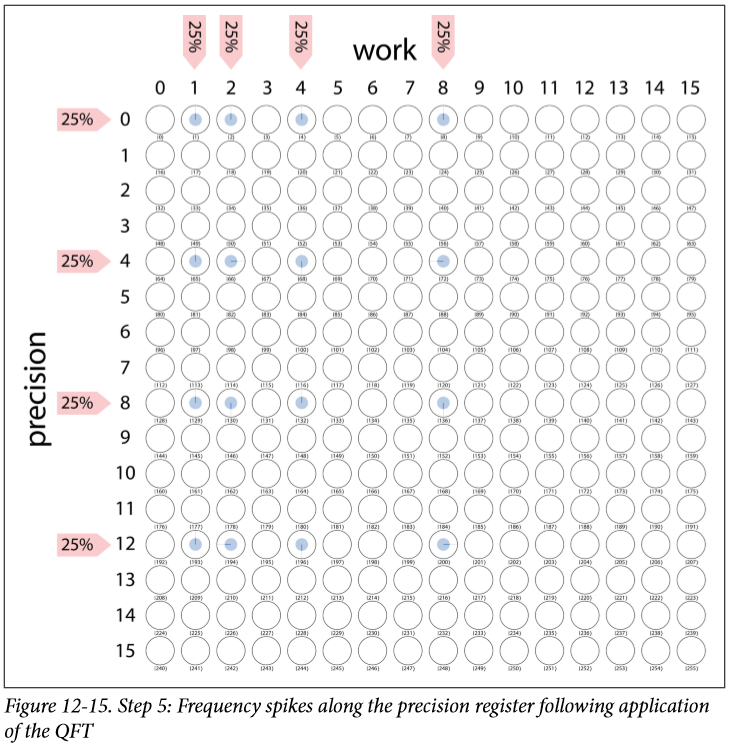
- Step 6: Read the Quantum Result
测量,我们测量的结果可能是0、4、8、12中的任意一个,他们是等概率25%
- Step 7: Digital Logic
function ShorLogic(N, repeat_period, coprime) { // Given the repeat period, find the actual factors
var ar2 = Math.pow(coprime, repeat_period / 2.0);
var factor1 = gcd(N, ar2 - 1);
var factor2 = gcd(N, ar2 + 1);
return [factor1, factor2];
}
把4丢到这里面去算,得到的结果是3,5
- Step 8: Check the Result
量子机器学习
在这里我们将要介绍三种QML应用:线性方程组的求解,量子主成分分析和量子支持向量机。
HHL解线性方程
线性方程很容易变成矩阵乘法的形式A→x⃗ =b⃗ A→x→=b→ ,求解线性方程也就是x⃗ =A−1b⃗ x→=A−1b→
而HHL提供了一种比共轭梯度下降法更快地方式来找矩阵的逆。
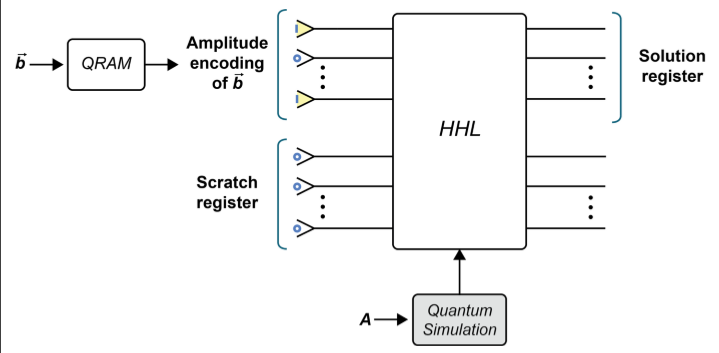
Scratch register 也就是辅助比特包含由HHL中的各种基元使用的许多临时量子位,所有临时量子位均以“ 0”状态准备。因为HHL处理定点(或浮点)数据并且涉及非平凡的算术运算(例如取平方根),所以我们需要大量的临时qubit。即使最简单的情况,这也使得HHL难以仿真。
当然如果我们得到了叠加态|x⟩|x⟩,也不是里面每一个数据都能读出来,但是在有的情况下,我们并不需要里面的每一个值,比如:
- 我们可能不需要|x⟩|x⟩的每个分量的值,而是他们平均值或者和
- 或者我们只想要比较一下看是否等于
- 或者|x⟩|x⟩只是程序下一部分的输入
这个算法的时间复杂度是O(x2s2ϵ−1logn)O(x2s2ϵ−1logn)
HHL算法适合于求解由稀疏,条件良好的矩阵表示的线性方程组。
那具体HHL又是怎么做的呢是怎么做到的?
HHL的灵感来自特征值分解来获得矩阵逆的信息,一个栗子:
A的特征向量为v1=[−0.7882,0.615]v1=[−0.7882,0.615] and v2=[−0.615,−0.788]v2=[−0.615,−0.788],对应的特征值为 λ1 = 0.438 and λ2 = 4.56, 那么,在特征基的表示下,我们可以把z改写成 [−0.788, −0.615],因为z⃗ =−0.788v⃗ 1−0.615v⃗ 2z→=−0.788v→1−0.615v→2
而A可以改写成:Λ=[0.438004.56]Λ=[0.438004.56]
现在求逆就很容易了,A−1=[10.4380014.56]=[2.281000.219]A−1=[10.4380014.56]=[2.281000.219]
那么,x⃗ =⎡⎣⎢⎢⎢⎢1λ1⋮0−⋱−0⋮1λn⎤⎦⎥⎥⎥⎥⎡⎣⎢⎢b˙1⋮b~n⎤⎦⎥⎥=⎡⎣⎢⎢⎢⎢1λ1b˙1⋮1λnb˙n⎤⎦⎥⎥⎥⎥x→=[1λ1−0⋮⋱⋮0−1λn][b˙1⋮b~n]=[1λ1b˙1⋮1λnb˙n]
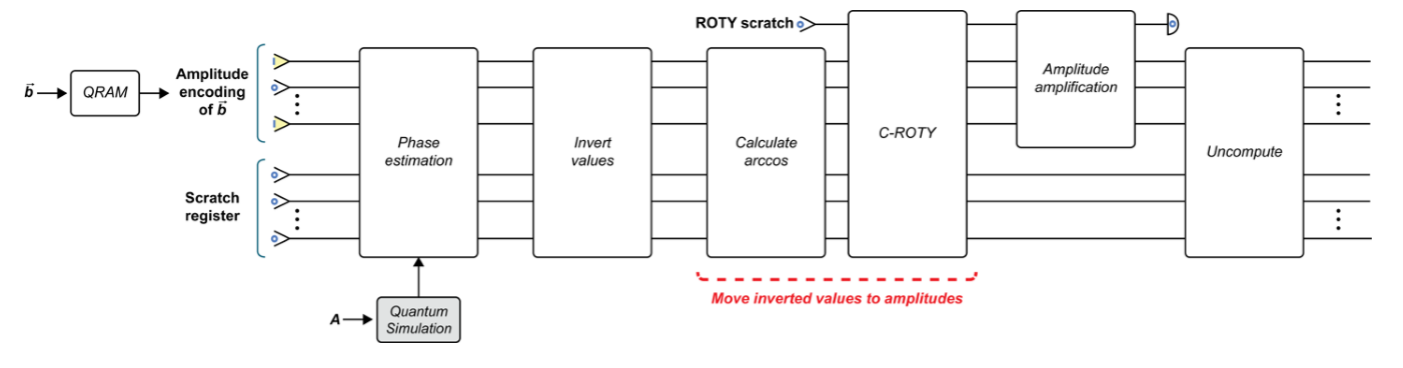
- Quantum simulation, QRAM, and phase estimation
- Invert values
- Move inverted values into amplitudes
- Amplitude amplification
- Uncompute
量子主成分分析
在量子之前,先了解一下什么是PAC,PCA通常用作预处理步骤,可以将一组输入的特征转换为新的、不相关的集合。 PCA产生的不相关功能可以根据它们编码的数据差异量进行排序。通过仅保留其中一些新功能,PCA通常被用作降维技术,仅保留前几个主要成分,可以在尽可能保留差异的情况下减少所需处理的数据量。
一个简单例子: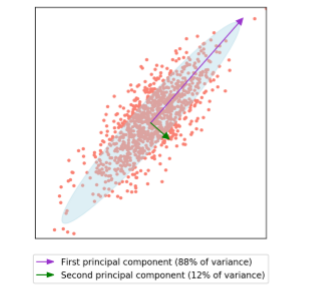
我们一般通过找到该协方差矩阵σ=1n−1XTXσ=1n−1XTX的特征分解来给出主成分,特征向量对应于主成分方向,而每个关联的特征值均与沿该主成分的数据方差成比例。
其中PCA中计算上最复杂的步骤是执行协方差矩阵的特征分解。
既然又是特征分解,那么我们可能觉得以下行为是有帮助的:
- 将数据的协方差矩阵表示为QPU操作。
- 对此QPU操作执行相位估计,以确定其特征值。
但是这同样也有问题:
-
Quantum simulation with σ
协方差矩阵很少能满足量子模拟技术的稀疏性要求,因此我们需要一种不同的方法来找到σ的QPU运算表示。
-
Input for phase estimation
相位估计有两个输入寄存器,我们必须使用其中之一来指定要为其关联本征相位(并由此获得本征值)的本征态。但是知道σ的任何特征向量正是我们要使用QPCA解决的问题的一部分。(HHL中可以解决是因为我们有|b⟩|b⟩)
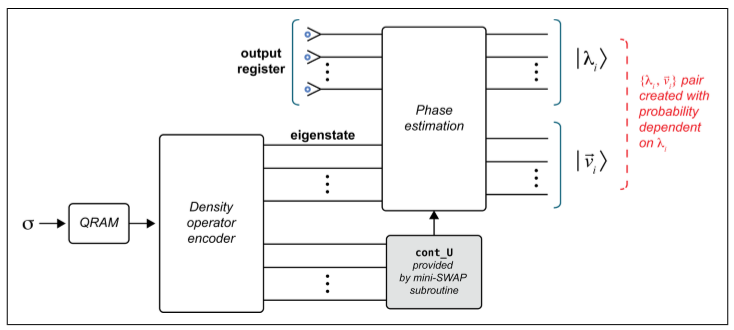
解决方案:
- 用mini-SWAP来改变矩阵的稀疏性,具体见 https://arxiv.org/abs/1307.0401
- σ的密度算符表示正好是我们相位估计的输入,如果这样的话,输出就正好是编码了的特征值。
![]()
量子支持向量机
支持向量机的主要目的是找到一个超平面,把左右两类数据给隔开,并且尽可能的,让这个平面离两边数据都远远的。
通过对偶问题转换,我们可以把SVM问题变成最小二乘优化问题。
变成这个问题后,我们的问题就又一次变成如何把这个现有的问题塞到HHL的接替框架里面。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号