量子隐形传态 Quantum Teleportation
量子隐形传态是量子纠缠的又一个应用。
隐形传态,所谓隐形的意思就是没有物质介质就传递了信息,在经典世界,传递信息要有介质,光、电磁波或者其他的什么,但是在量子的世界里,我可以把信息传递给你,并且不传递任何一个量子比特。
量子不能克隆原理
不能克隆就是说,没有任何一个U操作,可以输入\(|\psi\rangle\) 和 \(|0\rangle\) 然后得到输出 \(|\psi\rangle\) 和 \(|\psi\rangle\) 。
why?
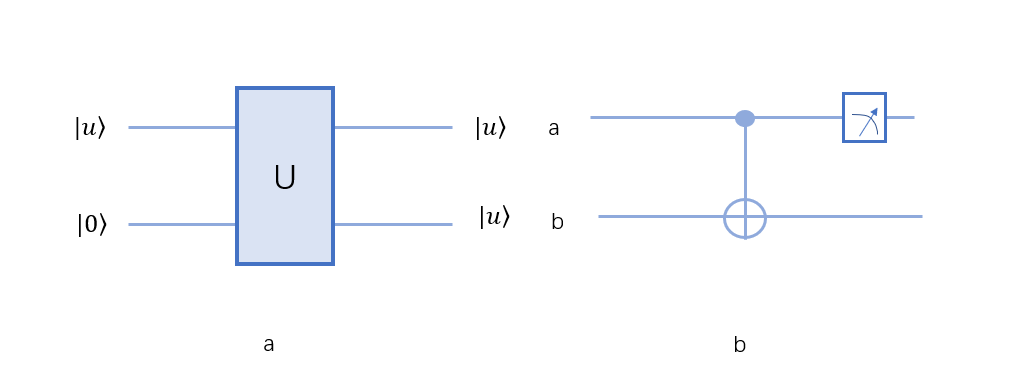
若是真的有这么一个操作算符,如图a,可以复制任意的量子比特 \(|u\rangle\) 我们希望的结果如下:
输入:\((\alpha_0 | 0\rangle +\alpha_1 | 1\rangle)|0\rangle\)
输出:\((\alpha_0 | 0\rangle +\alpha_1 | 1\rangle)(\alpha_0 | 0\rangle +\alpha_1 | 1\rangle)\)
另一方面
我们希望输入是\(|00\rangle\)输出也是\(|00\rangle\),当输入变成\(|10\rangle\)后,输出也就变成\(|11\rangle\)
而要以上两种情况相等,只有一种可能,即\(|u\rangle\)是\(|0\rangle\)或者\(|1\rangle\)的时候,但是这样,也就没有叠加态的,这样复制的,也就是一个普通的bit。
量子隐形传态
如果Alice要把一个她也不知道具体状态的量子态 \(|\psi\rangle=\alpha | 0\rangle +\beta | 1\rangle\) 的信息传给远方的Bob,她应该怎么办?
测量 $\alpha $ 和 \(\beta\) ?
因为Alice也不知道这个比特的具体状态,所以,Alice不能直接告诉Bob \(\alpha \beta\) 的值。
但是Alice也不能去测量,因为一旦测量了,就会导致量子态的坍缩,你只能得到 \(|0\rangle\) 或者 \(|1\rangle\) 而不能得到 $\alpha $ 和 \(\beta\) 的具体值。
但是你也不能复制大量的 \(|\psi\rangle\) 然后去看掉落到 \(|0\rangle\) 或者 \(|1\rangle\) 的概率,因为量子态不能被复制,用CNOT看似能能够copy量子态的信息,但是他们的状态是纠缠的,测量一个,另一个也就跟着坍缩了。
Teleportation with CNOT
图b是前面介绍过的CNOT门,有CNOT门,我们很容易就可以把 \(\alpha_0 | 00\rangle +\alpha_1 | 10\rangle\)变成 \(\alpha_0 | 00\rangle +\alpha_1 | 11\rangle\) 。
此时并没有被复制,因为第一个比特和第二个比特之间还是纠缠的,也就是说你测量第一个比特,第二个就会坍缩,你测量第二个,第一个也同理,信息并没有copy两份,所以量子不可复制原理没有被打破。
接下来我们要来处理第一个比特。
如果直接测量第一个比特,很明显,第二个比特就坍缩了。
但是测量还是要测的,不过不是在 \(| 0\rangle\) 、 \(| 1\rangle\) 基,而是在 \(| +\rangle\) 、 \(| -\rangle\) 基。
在 \(| +\rangle\) 、 \(| -\rangle\) 基对第一个比特测量:
如果测量的结果是 \(|+\rangle\) ,那么第二比特的状态就是 \(\alpha_0 | 0\rangle +\alpha_1 | 1\rangle\) ,正好是我们最初想要传递的态。
如果测量的结果是 \(|-\rangle\) ,那么第二比特的状态就是 \(\alpha_0 | 0\rangle -\alpha_1 | 1\rangle\) ,再经过Z门的翻转就是我们最初想要传递的态了。
Teleportation without CNOT
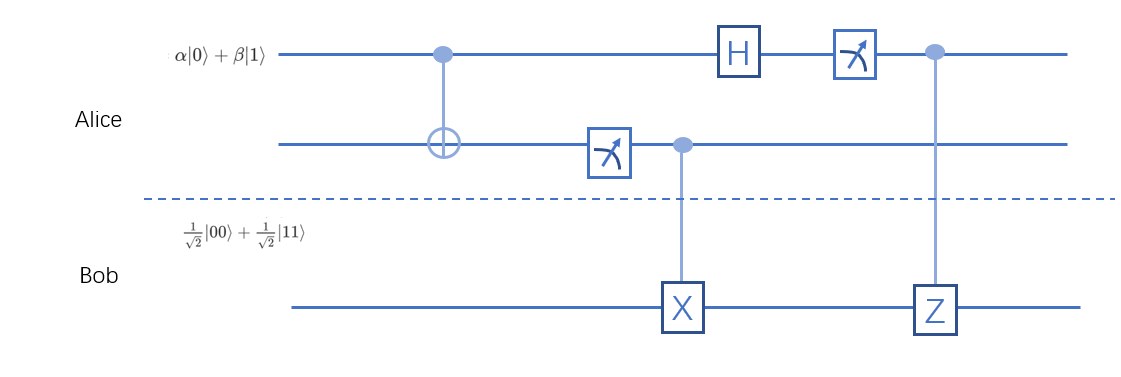
第一个量子比特是Alice想要把信息给Bob的 \(|\psi\rangle=\alpha | 0\rangle +\beta | 1\rangle\) ,第二个和第三个是一对纠缠的贝尔态量子比特 \(\frac{1}{\sqrt2}|00\rangle + \frac{1}{\sqrt2}|11\rangle\) ,将第二个比特放到Alice处,第三个在Bob那里。
最初三个比特的状态是 \(|\phi\rangle=\alpha \frac{1}{\sqrt2}| 000\rangle +\beta \frac{1}{\sqrt2}| 100\rangle+\alpha \frac{1}{\sqrt2}| 011\rangle +\beta \frac{1}{\sqrt2}| 111\rangle\)
经过CNOT门,现在的状态 \(|\phi\rangle=\alpha \frac{1}{\sqrt2}| 000\rangle +\beta \frac{1}{\sqrt2}| 110\rangle+\alpha \frac{1}{\sqrt2}| 011\rangle +\beta \frac{1}{\sqrt2}| 101\rangle\)
在\(| 0\rangle\)、\(| 1\rangle\)基测量第二个比特:
如果测量得到的结果是 \(|0 \rangle\) ,那么接下来的第一个比特和第三个比特的状态是:\(|\phi_0\rangle=\alpha | 00\rangle +\beta | 11\rangle\)
如果测量得到的结果是 \(|1 \rangle\) ,那么接下来的第一个比特和第三个比特的状态是:\(|\phi_1\rangle=\alpha | 01\rangle +\beta | 10\rangle\) ,那么对第三个比特作用一个X门,X门的作用是\(| 0\rangle\)、\(| 1\rangle\)互换,在这之后 \(|\phi_1\rangle=\alpha | 00\rangle +\beta | 11\rangle\) ,和 \(|\phi_0 \rangle\) 统一
对第一个量子比特作用H门,然后在\(| 0\rangle\)、\(| 1\rangle\)基测量。(事实上,加上H门,然后测量在\(| 0\rangle\)、\(| 1\rangle\)基测量得到的结果和直接在 \(| +\rangle\) 、 \(| -\rangle\) 基测量的效果是一样的)
H门之后的状态:
\(|\phi\rangle=\alpha (\frac{1}{\sqrt2}|0\rangle + \frac{1}{\sqrt2}|1\rangle)| 0\rangle +\beta (\frac{1}{\sqrt2}|0\rangle - \frac{1}{\sqrt2}|1\rangle)| 1\rangle\)
\(|\phi\rangle=|0\rangle(\frac{\alpha}{\sqrt2}|0\rangle+\frac{\beta}{\sqrt2}|1\rangle)+|1\rangle(\frac{\alpha}{\sqrt2}|0\rangle-\frac{\beta}{\sqrt2}|1\rangle)\)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号