微积分奇观之计算曲线的平均高度

下图是某地的气温变化图，

我们一般所说的平均气温实际上只是取几个时刻的气温值后求其平均而已，但准确来讲是不是应该将给定时段内所有的（无数个）气温值的平均值给计算出来才算得上是平均气温的准确值呢？这就引入了本文所要解决的问题——把连续曲线上所有点的高度的平均值（平均高度）给求出来，其中曲线上各点的高度规定为该处的函数值。乍看之下这好像是个不可能的任务，因为曲线上无数个点对应的无限多个高度我们是加不过来的，更别提用总和除以总数来计算平均高度了——不得不承认这个事实，但如果换成有限多个高度，那么其平均值自然是可以求出来的，本文就将从此入手来求出这无限多个高度的平均值。

在上图中将[a,b]等分成n个小区间，也即在[a,b]上等距离地取n+1个不同的点x_i，即

a = x₀ < x₁ < x₂ < ⋯ < x_i − 1 < x_i < ⋯ < x_n = b （其中i = 1, 2, …, n）

相邻两个分点构成的区间[x_i − 1, x_i]的长度是$\frac{b - a}{n}$，

¹

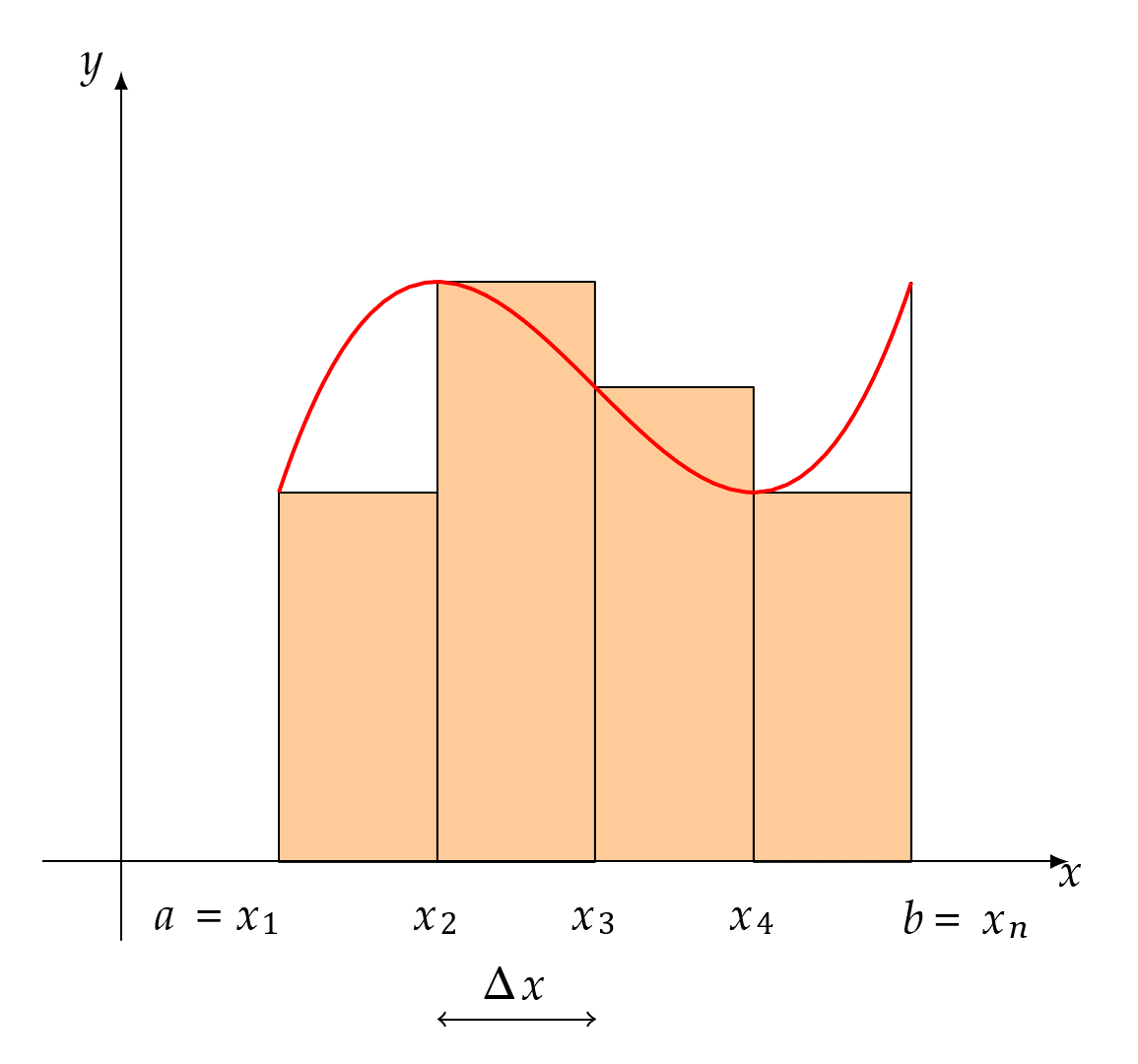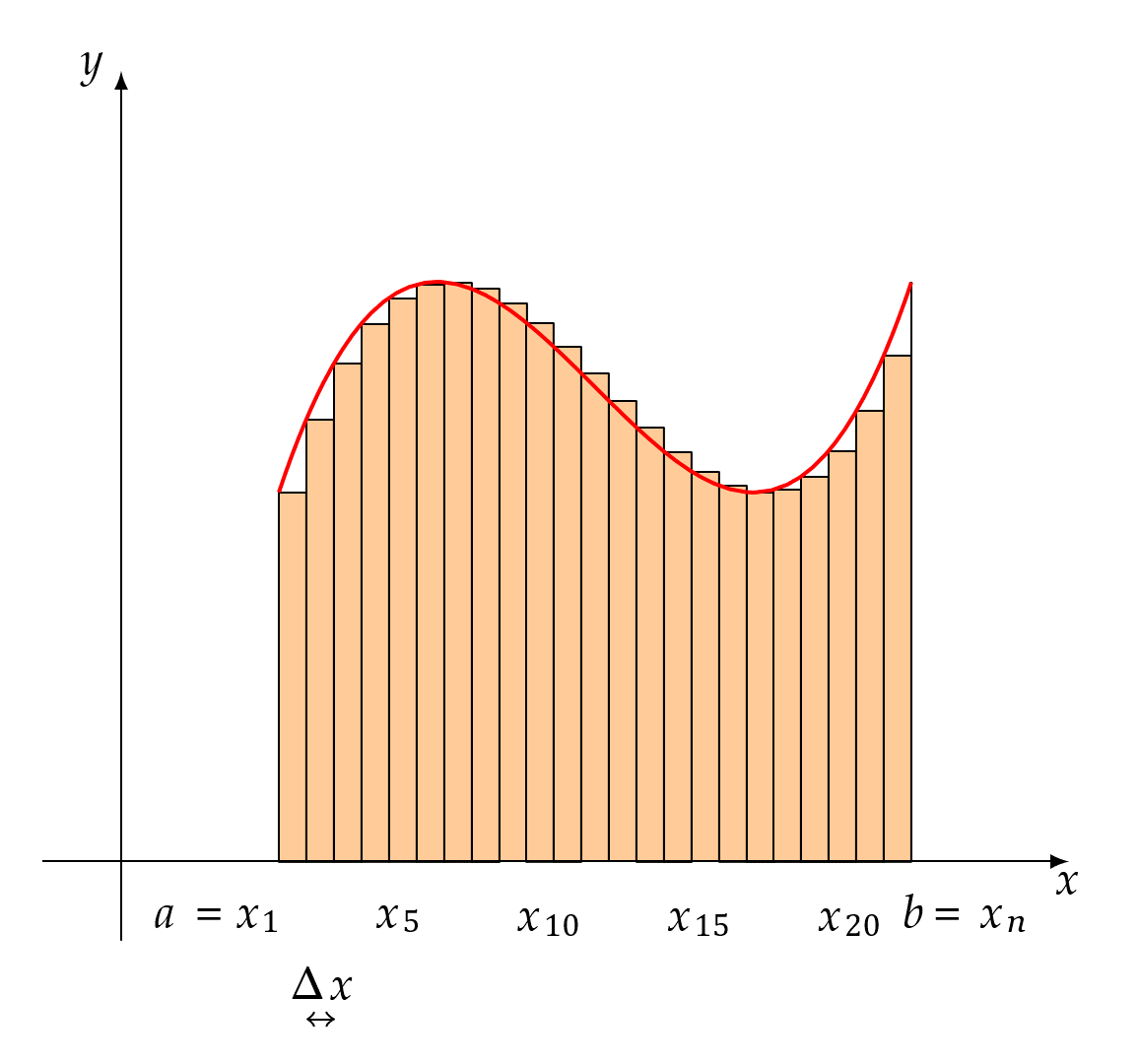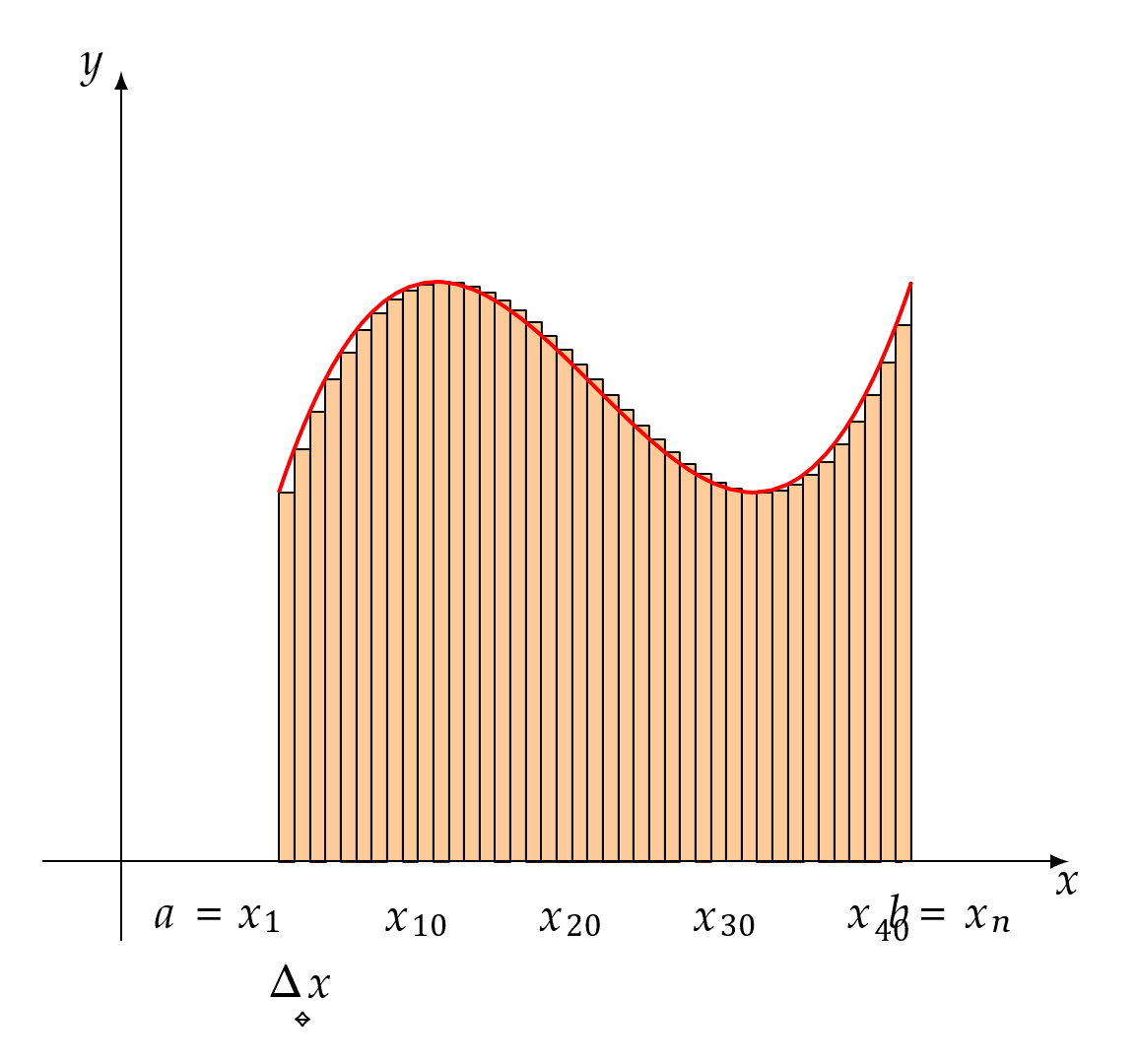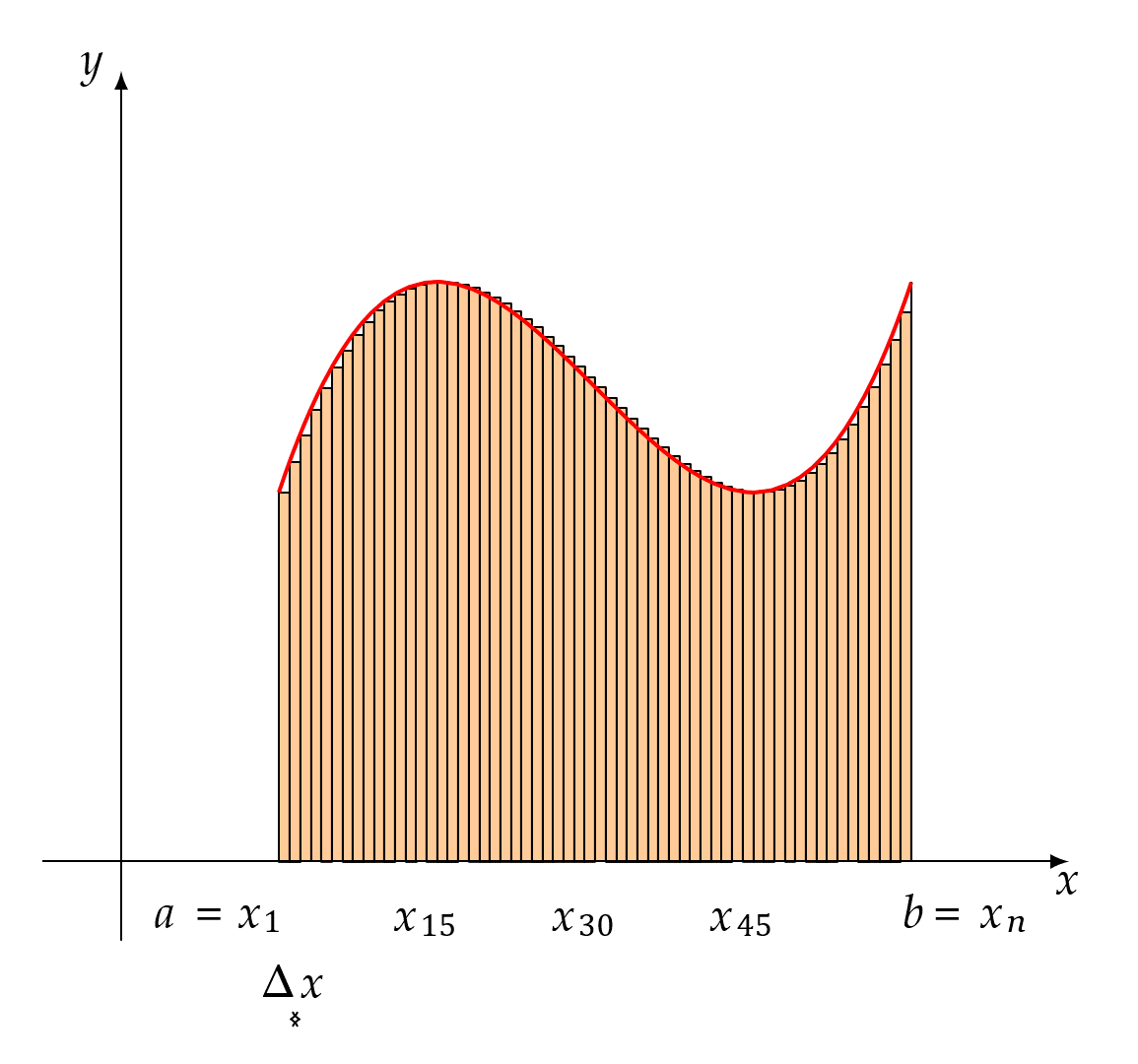
当n足够大的时候，每个这种小区间的长度就会足够小，以至于小区间内任意一点ξ_i对应的函数值f(ξ_i)和里面其它x对应的函数值的差别也就不会很大，这时就可用f(ξ_i)来代表该小区间内点的高度，当n越大，f(ξ_i)就越能代表该小区间内点的高度，我们就定在不断等分过程中这n个点的平均高度的极限

$$\lim_{n \rightarrow \infty}\frac{f\left( \xi_{1} \right) + f\left( \xi_{2} \right) + \cdots + f\left( \xi_{n} \right)}{n}$$

为连续曲线f(x)于[a,b]上所有点的平均高度。又因为连续曲线f(x)于[a,b]上构成的曲边梯形面积是

$$\begin{matrix} \lim_{\lambda \rightarrow 0}\left( f\left( \xi_{1} \right)\text{Δx} + f\left( \xi_{2} \right)\text{Δx} + \cdots + f\left( \xi_{n} \right)\text{Δx} \right) = \lim_{\lambda \rightarrow 0}{\sum_{i = 1}^{n}{f\left( \xi_{i} \right)\text{Δx} = S}} \\ \end{matrix}$$

其中Δx是每个小区间的长度$\frac{b - a}{n}$，借助这个条件上述平均高度可以有进一步的计算结果²，

$${\displaystyle {\begin{aligned}\lim _{n \rightarrow \infty} \frac{f\left(\xi_{1}\right)+f\left(\xi_{2}\right)+\cdots+f\left(\xi_{n}\right)}{n}&=\lim _{n \rightarrow \infty} \frac{f\left(\xi_{1}\right) \Delta x+f\left(\xi_{2}\right) \Delta x+\cdots+f\left(\xi_{n}\right) \Delta x}{n \Delta x}\\&=\frac{\lim _{n \rightarrow \infty}\left(f\left(\xi_{1}\right) \Delta x+f\left(\xi_{2}\right) \Delta x+\cdots+f\left(\xi_{n}\right) \Delta x\right)}{\lim _{n \rightarrow \infty}(n \Delta x)}\\&=\frac{S}{\lim _{n \rightarrow \infty}\left(n \times \frac{b-a}{n}\right)}\\&=\frac{S}{b-a}\end{aligned}}}$$

S是曲边梯形的面积，而b − a是曲边梯形的底边长度，所以求出来的连续曲线f(x)于[a,b]上所有点的平均高度$\frac{S}{b - a}$就相当于是与曲边梯形面积相等且共底的矩形的高度。

下面举三个例子来看看这个方法求出来的连续曲线上所有点的平均高度与我们的直觉的关系：

1. 常数函数c于[a,b]上所有点的平均高度显然是$\lim_{n \rightarrow \infty}\frac{f(\xi_{1}) + f(\xi_{2}) + \cdots + f(\xi_{n})}{n} = c$，这与我们的直觉一致；

2. y=2x于[1,5]上的所有点的平均高度

   

   从直观上来看我们极有可能认为这个平均高度是$\frac{左端点的高度 + 右端点的高度}{2} = \frac{2 \times 1 + 2 \times 5}{2} = 6$，用我们计算平均高度的方法得到这个值等于梯形的面积$\frac{(2 + 10) \cdot 4}{2} = 24$除以区间[1,5]的长度4结果是$6 = \frac{24}{4}$，也和我们的直觉一致；

3. 我们可能会从直觉上认为$\frac{1}{4}$圆的图像于第一象限内所有点的平均高度是$\frac{1}{2}$，

   

   但根据我们上面的方法其平均高度是$\frac{\int_{0}^{1}{\sqrt{1 - x^{2}}\text{dx}}}{1} = \int_{0}^{1}{\sqrt{1 - x^{2}}\text{dx}} = \frac{\pi}{4} \approx 0.79 > \frac{1}{2}$，那么我们的直觉错在哪里呢？$y = \sqrt{1 - x^{2}} = \frac{1}{2}$时，$x = \frac{\sqrt{3}}{2} \approx 87\%$，所以$\sqrt{1 - x^{2}}$于[0,$\ \frac{\sqrt{3}}{2}$]的图像上每个点的高度都大于等于$\frac{1}{2}$，这大约占了函数图像的87%，但我们还认为整个（100%）函数图像上所有点的高度是$\frac{1}{2}$，这就低估了这个平均高度了。

所以上述求连续曲线上所有点的平均高度的方法有符合直觉的地方，有时虽不符合直觉但也有其合理性。最后，通过本文的方法我们把坐标系上一条连续曲线的平均高度给计算出来了，这是不是很不可思议呢？

---

1. 由于本人不擅长数学绘图，所以本动图和情景有点不太符合，有能力者可联系我一起出更好的图↩

2. Introduction to Calculus and Analysis Volume I, Reprint of the 1989 edition, Richard Courant, Fritz John, p141↩