【题解】CF522D Closest Equals

题面

我的老师讲这种类型的题时用了一个很直观的方法。先%我的老师

观察发现本题可以用 map 将所有临近的相同的点预处理出来，得到若干条线段，于是问题转化为询问一个区间内完整线段的最小长度。

假如坐标轴上有这些线段：

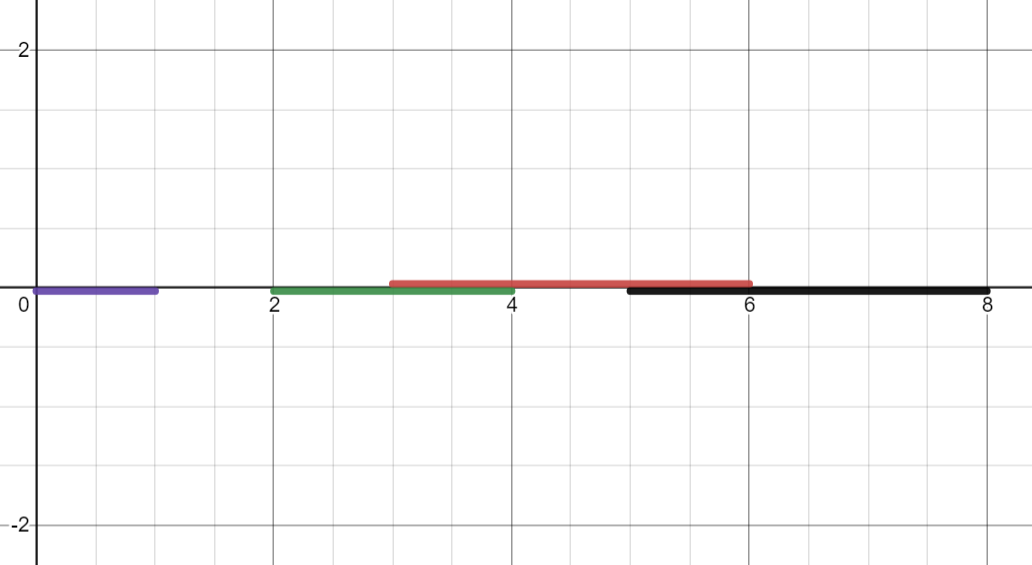
我们不妨将线段转化为平面中的一些点，其中左端点为横坐标，右端点为纵坐标：

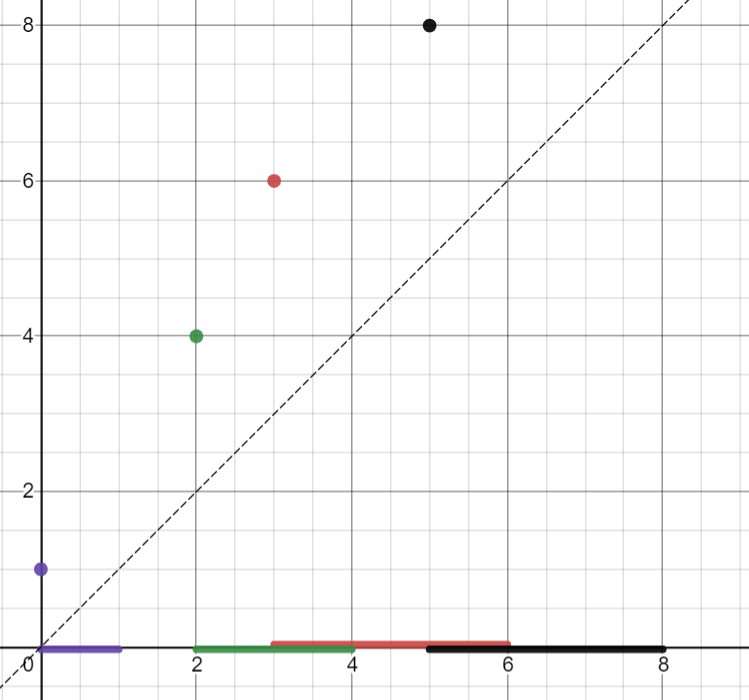
那么当我们求如图所示的区间时：

也就是求下图这个平面中阴影部分的点中 \(r-l\) 最小的那个点。

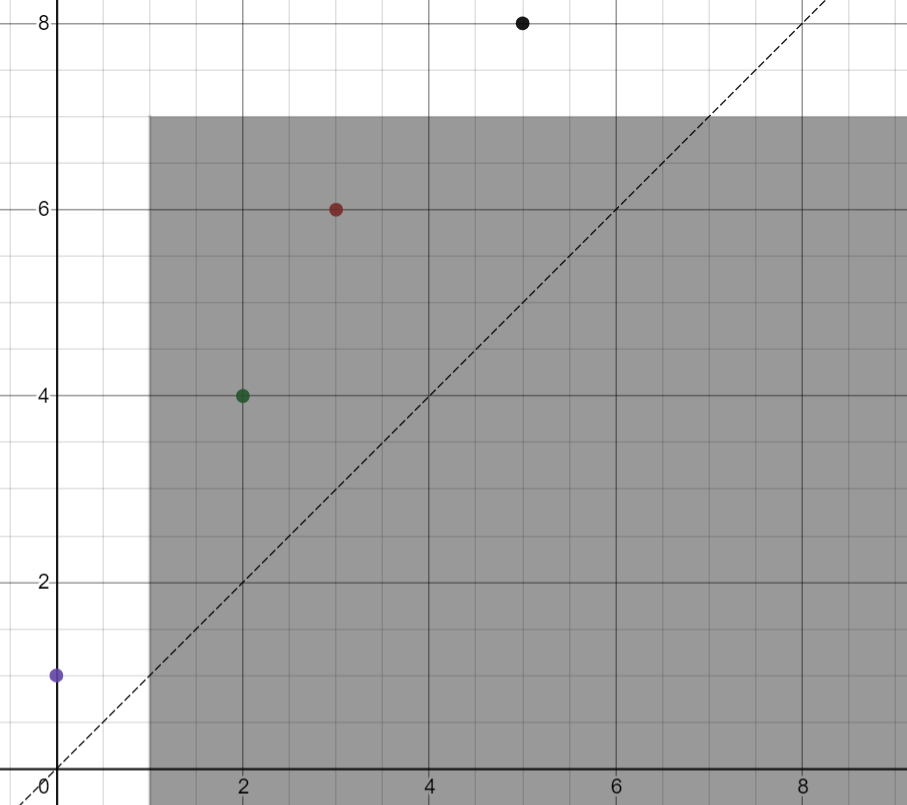
答案是不是呼之欲出了？我们可以用扫描线求解。

首先预处理出所有的线段，用 vector 存入平面中所有的x对应的纵坐标 y ，也就是所有的点；将扫描线从右向左扫描横坐标，用树状数组维护纵坐标为 \(1\) 到 \(y\) 中 \(y-x\) 的最小值，每次离线回答询问时便可以保证 \(x\geq l_j ,y\leq r_j\)。

代码：

#include <bits/stdc++.h>
using namespace std;

const int maxn=5e5+5;
map<int,int> last;
vector<int> g[maxn];
int n,a[maxn],m;
int C[maxn],id[maxn];
int l[maxn],r[maxn];
int ret[maxn];

bool cmp(int i,int j){
	return l[i]>l[j];
}

int update(int x,int p){
	while(x<=n){
		C[x]=min(C[x],p);
		x+=x&-x;
	}
}

int query(int x){
	int ret=0x3f3f3f3f;
	while(x){
		ret=min(C[x],ret);
		x-=x&-x;
	}
	return ret;
}//本题只需要维护小于等于x的最小值，故可以使用树状数组 

int main(){
	scanf("%d%d",&n,&m);
	memset(C,0x3f,sizeof C);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		if(last.count(a[i])){
			int x=last[a[i]];
			g[x].push_back(i);
		}
		last[a[i]]=i;
	}//寻找临近的点，预处理线段 
	for(int i=1;i<=m;i++){
		scanf("%d%d",&l[i],&r[i]);
		id[i]=i;
	}
	sort(id+1,id+m+1,cmp);//准备离线询问 
	int x=n;//扫描线 
	for(int k=1;k<=m;k++){
		int i=id[k];
		while(x>=l[i]){//向左扫，更新答案 
			for(int j=0;j<g[x].size();j++){
				int y=g[x][j];
				update(y,y-x);
			}
			x--;
		}
		ret[i]=query(r[i]);//回答询问 
	}
	for(int j=1;j<=m;j++){
		if(ret[j]==0x3f3f3f3f) printf("-1\n");
		else printf("%d\n",ret[j]);
	}
	return 0;
}