轻松易懂的莫队算法
莫队算法是一个可以离线处理区间信息的算法,通过离线+分块的方法将区间问题高效处理,在OI竞赛中十分常用。
一、基本思想
已经说过了,基本思想就是离线加分块。那么我们该如何通过莫队算法处理离线的询问呢?
对于一个我们已经处理好信息的区间 \([l,r]\) ,假如我们可以逐步移动左右端点更新信息,那么一个新区间 \([l',r']\) 的信息就可以通过若干次移动左右端点处理出来。
单次移动更新的代码示意:
while(L<l[i]) erase(a[L++]);
while(L>l[i]) add(a[--L]);
while(R<r[i]) add(a[++R]);
while(R>r[i]) erase(a[R--]);
//L,R为当前已经处理好的区间,l[i],r[i]为某一次的询问。
//在拓展L,R左右端点的同时,增加/删除信息。
为了可视化这一过程,我们将区间转化为平面内的一个点,用横坐标表示左端点,纵坐标表示区间右端点。区间的更新可以看作为平面内一个点的移动,从一个点移动到另一个点的代价为这两点的曼哈顿距离。
假如我们有若干个待处理区间,那么在平面内就是:
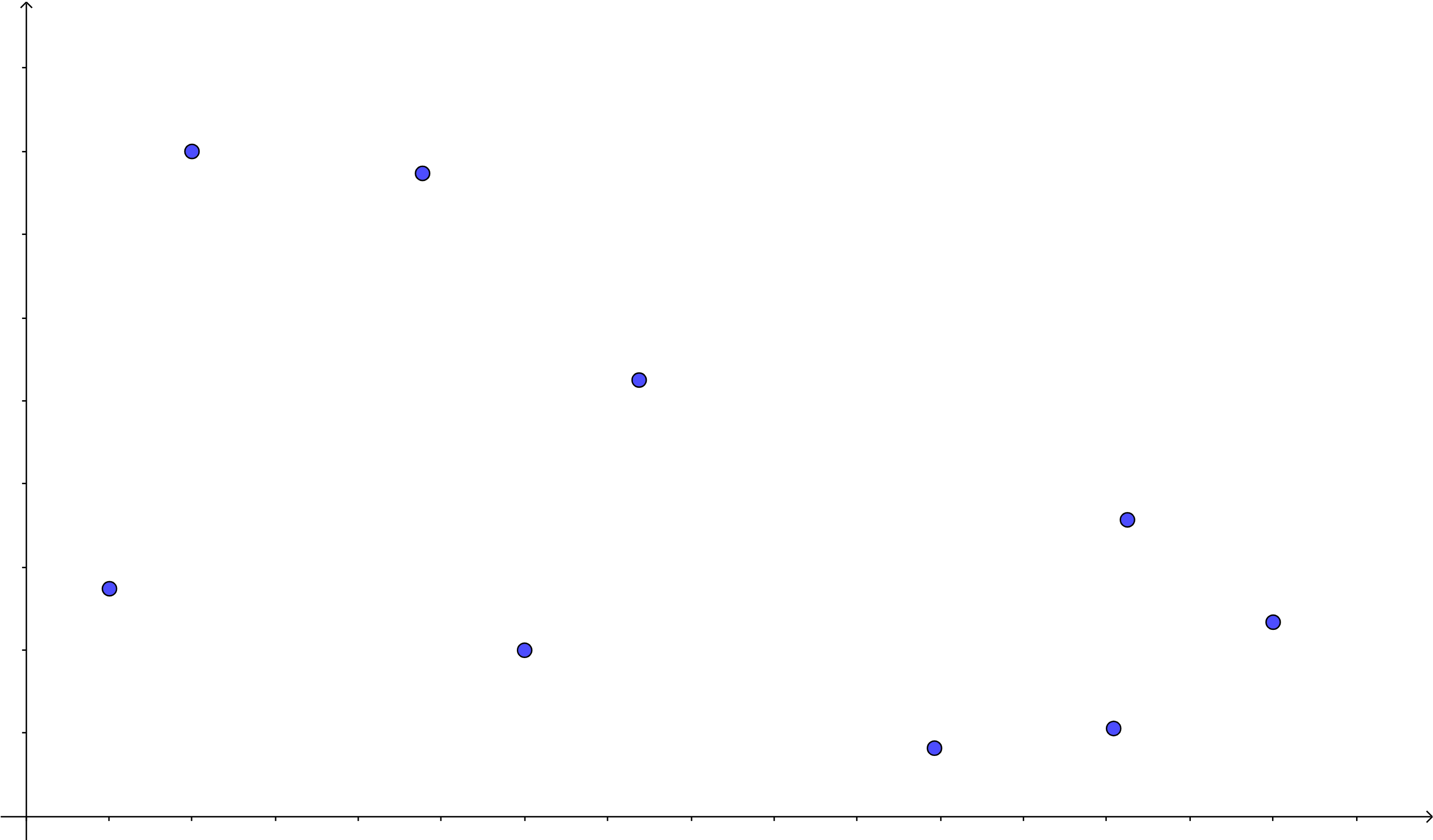
我们要处理所有的区间,也就是要找到一条路径把所有点串起来。我们就要考虑如何规划移动路线使得移动的代价尽量小。
这样,我们可以考虑按照点的横坐标均分成若干块,
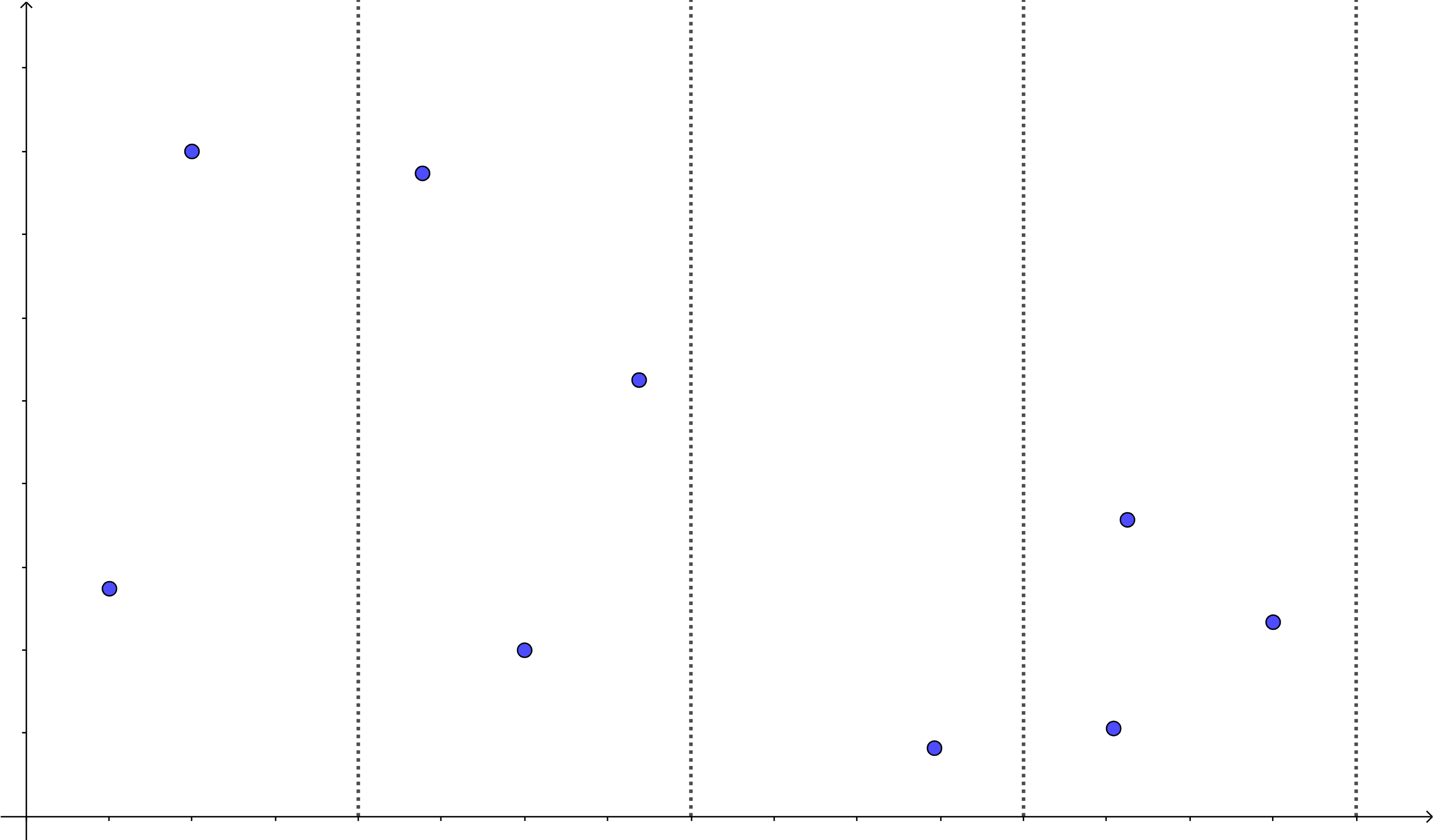
我们按照次序依次处理每个块内的点,对于每个块的点,我们按照纵坐标从小到大处理。也就是,不同块按横坐标排序,同一块按纵坐标升序排序。
bool cmp(int i,int j){
if(l[i]/k==l[j]/k) return r[i]<r[j];
return l[i]<l[j];
}//k是块的大小。
将这个过程可视化,就是这样的:
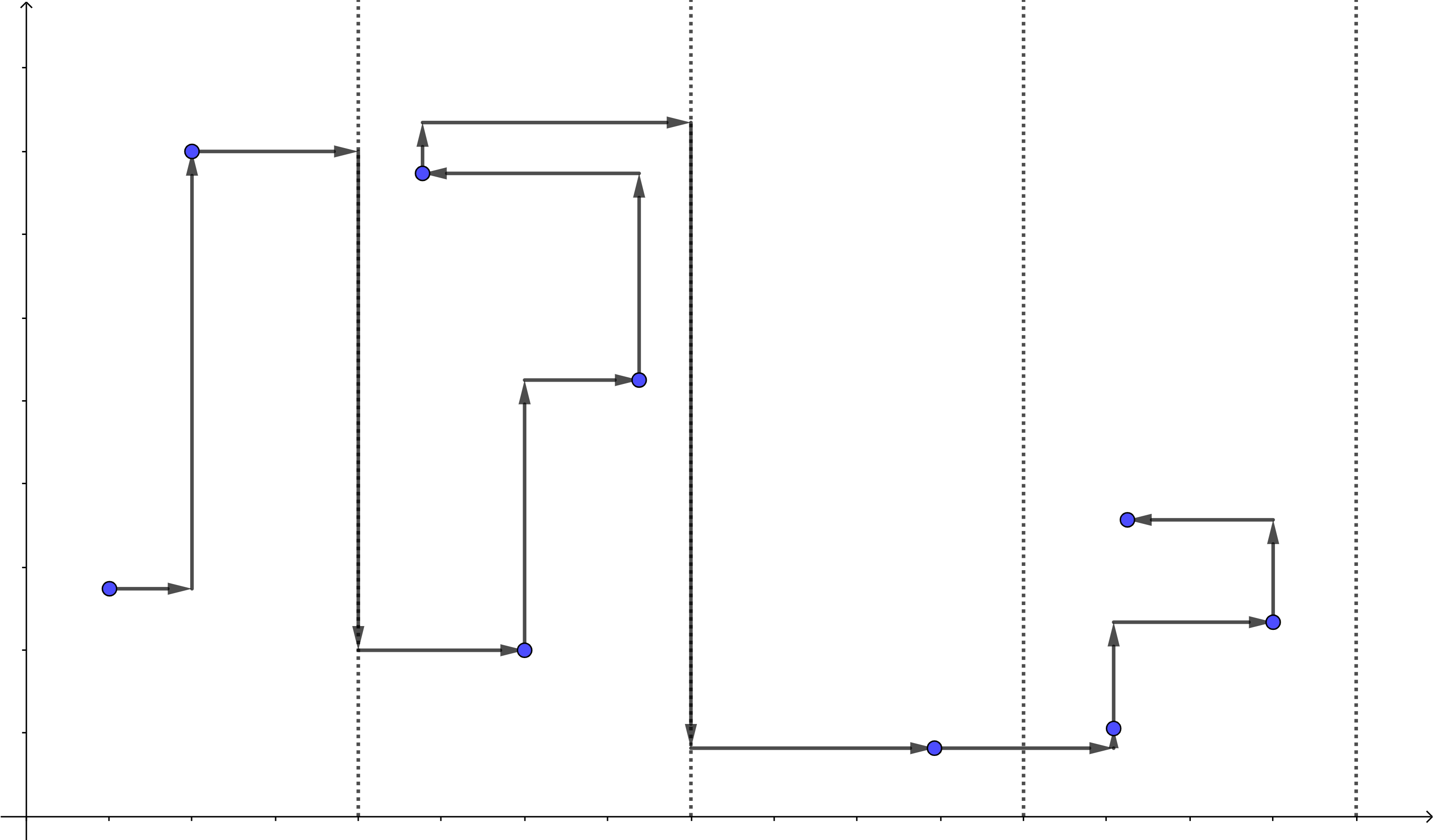
看上去不错,但是这样做的效率如何?又该怎么分块合适?
我们不妨设横坐标分块的大小为 \(k\) ,序列长度为 \(n\) ,有 \(m\) 个询问。分别考虑横坐标和纵坐标移动的时间复杂度。
对横坐标而言,我们已经分好了块,于是两个询问之间横坐标的移动复杂度一定不超过 \(O(k)\) 。故移动横坐标的复杂度为 \(O(mk)\)。
至于纵坐标的移动,单块内移动复杂度不会超过 \(O(n)\) ,所以纵坐标移动的复杂度为 \(O(n\frac{n}{k})=O(\frac{n^2}{k})\)。
于是莫队算法总的时间复杂度为
根据均值不等式,当且仅当 \(mk=\frac{n^2}{k}\) 即 \(k=\frac{n}{\sqrt m}\) 时等号成立。一般来说 \(n\),\(m\) 同阶,所以块的大小取 \(\sqrt n\) 时,莫队算法复杂度为 \(O(n \sqrt n)\)。这个复杂度在大多数情况下相当优秀。
此外普通莫队还有一个小优化:对于奇数块询问按右端点升序排序,偶数块按右端点降序排序。结合示意图,应该能明白其背后原理。
这只是莫队的最基本思想。在 OI 界,莫队算法随着 OIer 们的探索不断衍生出各种变体。接下来我们来看看莫队算法有哪些强力的拓展版本吧。
二、衍生算法
(1)带修莫队
来看一个例题:
有一个序列,\(m\) 个操作,包括:
- 修改序列上某一位的数字
- 询问区间 \([l,r]\) 中不同数字的个数。
这个和普通莫队相比,多了修改的操作。莫队算法该如何处理这样的修改询问呢?
啊其实很简单,这个修改其实是随着时间进行的,那么我们只要对修改和询问标记上一个时间维度,在询问间移动时同时移动时间,更新时间信息。
这样就有三个维度了,一个询问的信息为 \((l,r,t)\) 。我们以左端点为横坐标,右端点为纵坐标,时间为竖坐标。同样地,我们对三维空间中的点进行分块:
bool cmp(int i,int j){
if(l[i]/k!=l[j]/k) return l[i]<l[j];
if(r[i]/k!=r[j]/k) return r[i]<r[j];
return t[i]<t[j];
}//l,r,t分别为左端点、右端点与时间。k是分块大小。
这样分块起到了一个什么效果?我们把 \(xOy\) 面分为了若干个大小为 \(k^2\) 的块,整个空间被我们分为了若干个底面面积为 \(k^2\) 的柱体。我们以横坐标为第一关键字、纵坐标为第二关键字处理这些空间块。对于每个柱体,按竖坐标从小到大处理每个点。
分析一下这个算法的复杂度:
为了简便计算,序列长度为 \(n\)、询问个数记为 \(m\) ,时间记为 \(t\) ,分块大小为 \(k\) 。
横坐标的移动:\(O(mk)\)
纵坐标的移动:\(O(k\frac{n^2}{k^2}+mk)=O(\frac{n^2}{k}+mk)\)
竖坐标的移动:\(O(\frac{n^2t}{k^2})\)
我们来分析一下如何分块:记 \(k=n^\alpha\),认为 \(n\),\(m\),\(t\) 同阶,均为 \(n\)。
总时间复杂度为:
当 \(\max\{1+\alpha,2-\alpha,3-2\alpha\}\) 最小时,\(\alpha=\frac{2}{3}\)。故分块大小应为 \(\sqrt[3]{n^2}\)。此时时间复杂度为 \(O(n\sqrt[3]{n^2})\)。
(2)树上莫队
普通莫队只能处理序列上的区间问题。假如把问题放到树上,那么还怎么解决呢?
给出一棵节点数为 \(n\) 的树。每个点有一个颜色 \(a_i\) ,给出 \(m\) 个询问,求 \(u\),\(v\) 两点路径上有多少种不同的颜色。
很自然地,我们会想把一棵树转变为一个序列,以便莫队算法处理。
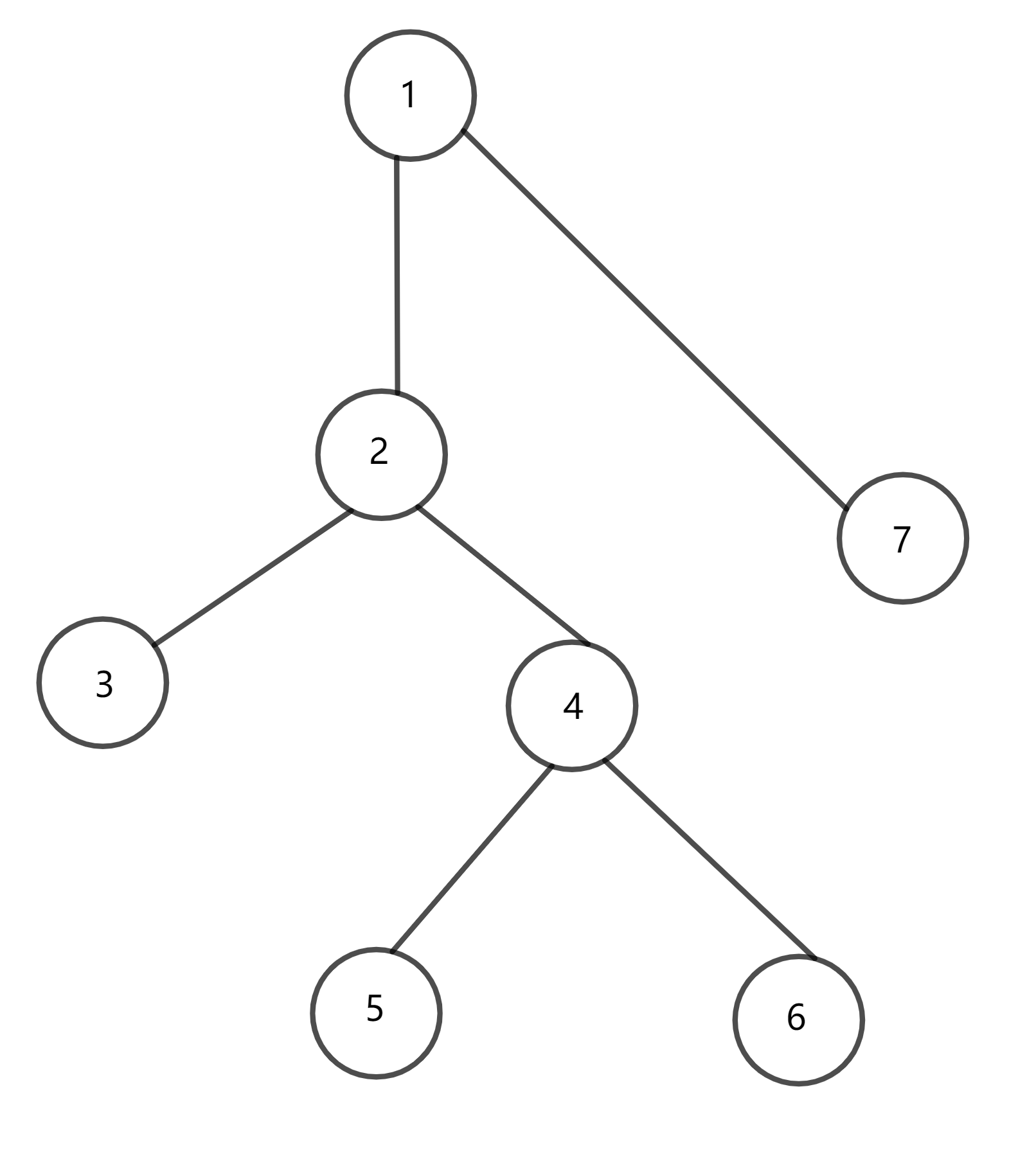
这是一棵树,我们可以用欧拉序将其转变为一个序列。欧拉序就是从根结点出发,按深度优先搜索的顺序时经过所有点的顺序。与dfs序不同,一个点会分别在进入和退出时加入序列。
比如上面这棵树,它的dfs序为1 2 3 4 5 6 7,
欧拉序却为1 2 3 3 4 5 5 6 6 4 2 7 7 1。
将结点 \(u\) 的进入、退出时间分别记为 \(in_u\) ,\(out_u\) 。我们可以发现任意两点之间的路径只有两种情况(下文的讨论保证保证 \(u\) 比 \(v\) 先被遍历):
1、\(u,v\) 为祖先/子孙关系。那么 \(u\) \(v\) 之间的路径是一条自上而下的链。以从 \(1\) 到 \(4\) 的路径为例,我们观察一下 \(in_1\) 到 \(in4\) 之间的欧拉序:1 2 3 3 4。发现 \(3\) 出现了两次,因为 \(3\) 并不在路径上,中途退出了。对于这种情况,我们处理 \([in_u,in_v]\) 这个区间的信息即可。
2、\(u\),\(v\) 在同一棵子树里。那么它们之间的路径会经过 \(lca(u,v)\)。以 \(3\) 和 \(6\) 为例,观察 \(out_3\) 到 \(in_6\) 之间的欧拉序:3 4 5 5 6。\(5\) 不在路径上,所以出现了两次。但有没有发现少了点啥?\(lca(3,6)\) 也就是 \(2\) 不见惹。所以处理询问时要把 \(lca(u,v)\) 的信息加上。
综合以上两种情况,我们发现,对于已经询问了的区间,假如新加入区间的点已经被统计过,那么将该点的信息去掉;反之加入信息。我们可以这样写 update 函数:
void update(int u) {
int x=lst[u];
vis[x]?erase(c[x]):add(c[x]);
vis[x]^=1;
}//lst是欧拉序。vis记录某个点是否出现过。
其它和普通莫队没什么区别了。
(3)回滚莫队
上述问题都有着区间可自由拓展的特性,但有些问题让区间只能单向操作。
来看这道题:
给出一个长度为 \(n\) 的序列,有 \(m\) 个询问,每次询问一个区间 \([l,r]\) ,求其中出现次数最多的数字个数。
容易发现,当区间向外拓展时,答案是很容易维护的;然而区间向内回退时却不能更新答案。这要求莫队在运行时只能 add 不能 erase。但这个难不倒 OIer 们,他们设计出了如下算法:
1、首先将所有询问按照左端点分块、右端点升序排序(同普通莫队)。假如 \(l,r\) 在同一个块内那就单独拎出来暴力算,因为怎么样也不会超过 \(O(k)\)。
2、假如一个新的询问的左端点在不同的块内了(也就是左端点在上一个块内的询问已经处理完),假如新的块为 \(A\),我们将左端点 \(L\) 重置为 \(A\) 的右端点加 \(1\) ,右端点 \(R\) 设置为 \(A\) 的右端点,并清除区间信息。此时区间为空。
3、右端点是升序,可以无脑拓展。右端点拓展出的信息要单独维护。每次询问之前,我们先把左端点重置为 \(A\) 的右端点加 \(1\) 并清空左端点拓展的信息,再作更新,回答询问。这就是回滚。
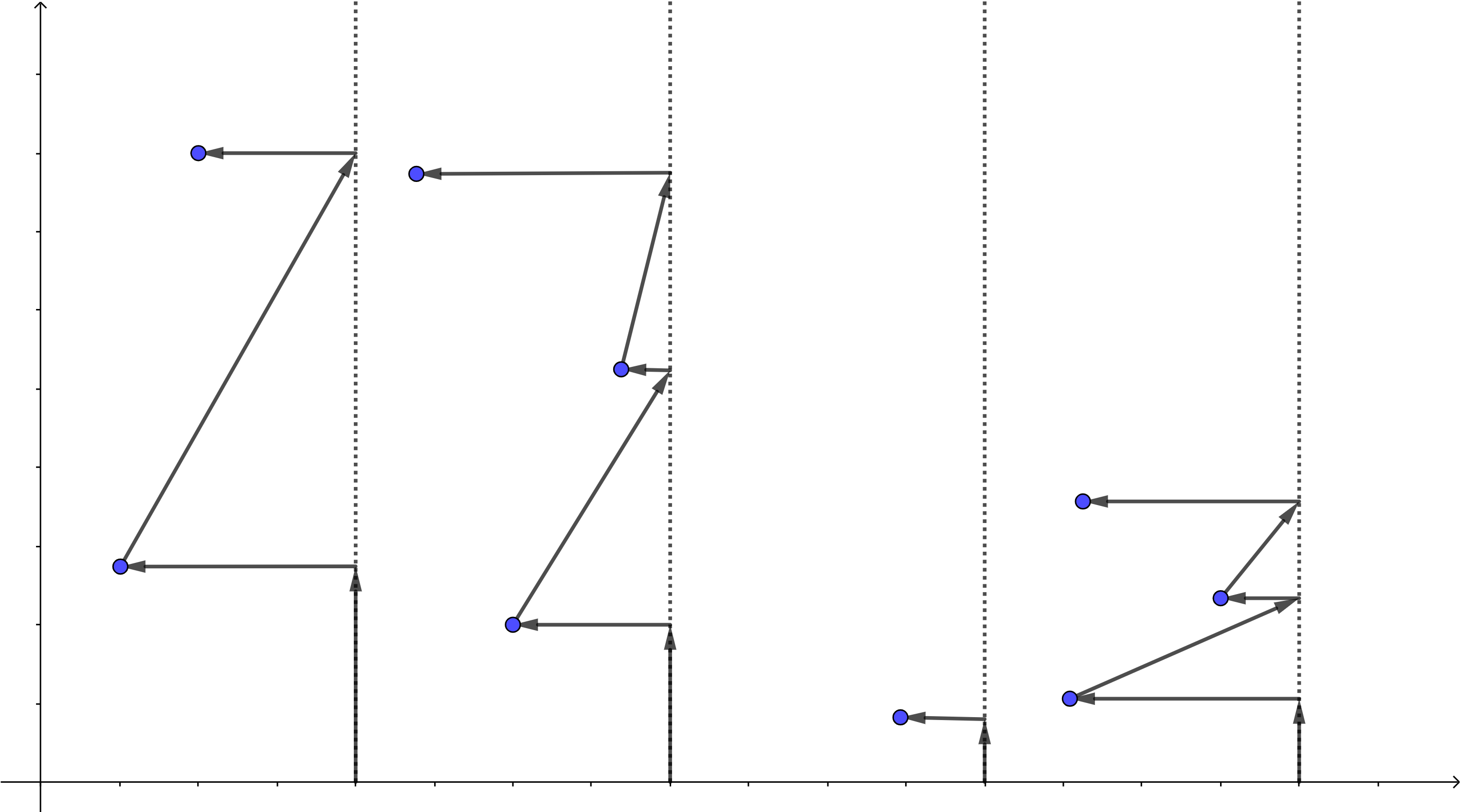
可以发现,每次询问后左端点都会回到块的右端。看样子多了很多操作,但仔细思考一下,其复杂度与普通莫队是一致的。分块大小也与普通莫队一致。所以回滚莫队复杂度依然为 \(O(n\sqrt n)\)。
三、强制在线
在线是不可能在线的,这辈子都不可能在线的。
感谢阅读!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号