LSTM学习
使用RNN预测文本
- 独热码:数量大,过于稀疏,映射之间是独立的,没有表现出关联性
- Embedding:一种单词编码方法,以低维向量实现了编码,这种编码通过神经网络训练优化,能表达出单词的相关性。
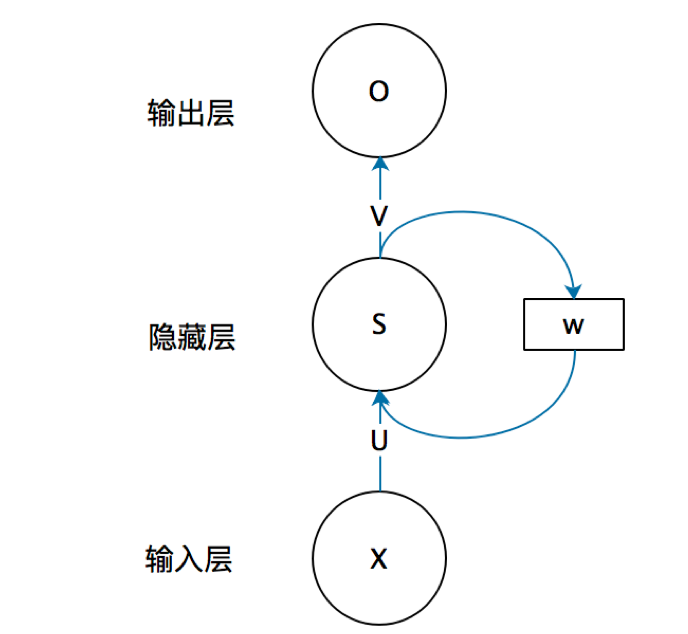
把上面有W的那个带箭头的圈去掉,它就变成了最普通的全连接神经网络。x是一个向量,它表示输入层的值(这里面没有画出来表示神经元节点的圆圈);s是一个向量,它表示隐藏层的值(这里隐藏层面画了一个节点,你也可以想象这一层其实是多个节点,节点数与向量s的维度相同);
U是输入层到隐藏层的权重矩阵,o也是一个向量,它表示输出层的值;V是隐藏层到输出层的权重矩阵。
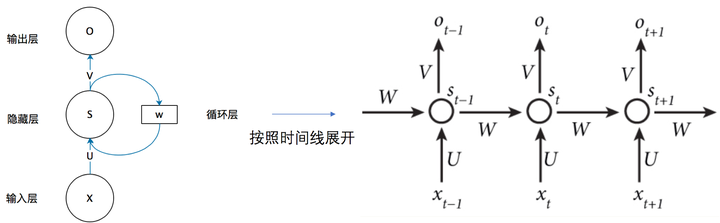
那么,现在我们来看看W是什么。循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x,还取决于上一次隐藏层的值s。权重矩阵 W就是隐藏层上一次的值作为这一次的输入的权重,给出这个抽象图对应的具体图
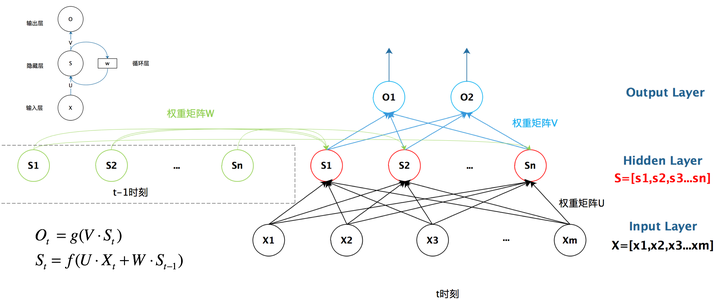
我们从上图就能够很清楚的看到,上一时刻的隐藏层是如何影响当前时刻的隐藏层的。
如果我们把上面的图展开,循环神经网络也可以画成下面这个样子:

import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN, Embedding
import matplotlib.pyplot as plt
import os
单词映射到数值id的词典
input_word='abcdefghijklmnopqrstuvwxyz'
w_to_id={
'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4,
'f': 5, 'g': 6, 'h': 7, 'i': 8, 'j': 9,
'k': 10, 'l': 11, 'm': 12, 'n': 13, 'o': 14,
'p': 15, 'q': 16, 'r': 17, 's': 18, 't': 19,
'u': 20, 'v': 21, 'w': 22, 'x': 23, 'y': 24, 'z': 25
}
training_set_scaled = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25]
x_train=[]
y_train=[]
for i in range(4,26):
x_train.append(training_set_scaled[i-4:i])
y_train.append(training_set_scaled[i])
x_train
[[0, 1, 2, 3],
[1, 2, 3, 4],
[2, 3, 4, 5],
[3, 4, 5, 6],
[4, 5, 6, 7],
[5, 6, 7, 8],
[6, 7, 8, 9],
[7, 8, 9, 10],
[8, 9, 10, 11],
[9, 10, 11, 12],
[10, 11, 12, 13],
[11, 12, 13, 14],
[12, 13, 14, 15],
[13, 14, 15, 16],
[14, 15, 16, 17],
[15, 16, 17, 18],
[16, 17, 18, 19],
[17, 18, 19, 20],
[18, 19, 20, 21],
[19, 20, 21, 22],
[20, 21, 22, 23],
[21, 22, 23, 24]]
y_train
[4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25]
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
np.random.seed(7)
x_train = np.reshape(x_train, (len(x_train), 4))
y_train = np.array(y_train)
x_train
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 2, 3, 4, 5],
[21, 22, 23, 24],
[19, 20, 21, 22],
[12, 13, 14, 15],
[11, 12, 13, 14],
[ 0, 1, 2, 3],
[20, 21, 22, 23],
[ 6, 7, 8, 9],
[18, 19, 20, 21],
[16, 17, 18, 19],
[13, 14, 15, 16],
[10, 11, 12, 13],
[17, 18, 19, 20],
[ 9, 10, 11, 12],
[ 8, 9, 10, 11],
[14, 15, 16, 17],
[ 7, 8, 9, 10],
[ 3, 4, 5, 6],
[ 4, 5, 6, 7],
[15, 16, 17, 18]])
建立rnn模型
model=tf.keras.Sequential([
Embedding(26,2),
SimpleRNN(10),
Dense(26,activation='softmax')
])
模型编译
model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
history = model.fit(x_train, y_train, batch_size=32, epochs=100)
Epoch 1/100
1/1 [==============================] - 4s 4s/step - loss: 3.2611 - sparse_categorical_accuracy: 0.0455
Epoch 2/100
1/1 [==============================] - 0s 11ms/step - loss: 3.2386 - sparse_categorical_accuracy: 0.0909
Epoch 3/100
1/1 [==============================] - 0s 9ms/step - loss: 3.2155 - sparse_categorical_accuracy: 0.0909
Epoch 4/100
1/1 [==============================] - 0s 8ms/step - loss: 3.1902 - sparse_categorical_accuracy: 0.0909
Epoch 5/100
1/1 [==============================] - 0s 7ms/step - loss: 3.1620 - sparse_categorical_accuracy: 0.0909
Epoch 6/100
1/1 [==============================] - 0s 9ms/step - loss: 3.1302 - sparse_categorical_accuracy: 0.0909
Epoch 7/100
1/1 [==============================] - 0s 9ms/step - loss: 3.0940 - sparse_categorical_accuracy: 0.0909
Epoch 8/100
1/1 [==============================] - 0s 7ms/step - loss: 3.0527 - sparse_categorical_accuracy: 0.1364
Epoch 9/100
1/1 [==============================] - 0s 8ms/step - loss: 3.0052 - sparse_categorical_accuracy: 0.2273
Epoch 10/100
1/1 [==============================] - 0s 8ms/step - loss: 2.9505 - sparse_categorical_accuracy: 0.3182
Epoch 11/100
1/1 [==============================] - 0s 6ms/step - loss: 2.8885 - sparse_categorical_accuracy: 0.3182
Epoch 12/100
1/1 [==============================] - 0s 6ms/step - loss: 2.8197 - sparse_categorical_accuracy: 0.3636
Epoch 13/100
1/1 [==============================] - 0s 7ms/step - loss: 2.7458 - sparse_categorical_accuracy: 0.3636
Epoch 14/100
1/1 [==============================] - 0s 7ms/step - loss: 2.6691 - sparse_categorical_accuracy: 0.3182
Epoch 15/100
1/1 [==============================] - 0s 11ms/step - loss: 2.5921 - sparse_categorical_accuracy: 0.3182
Epoch 16/100
1/1 [==============================] - 0s 16ms/step - loss: 2.5163 - sparse_categorical_accuracy: 0.3182
Epoch 17/100
1/1 [==============================] - 0s 12ms/step - loss: 2.4423 - sparse_categorical_accuracy: 0.3182
Epoch 18/100
1/1 [==============================] - 0s 11ms/step - loss: 2.3698 - sparse_categorical_accuracy: 0.3182
Epoch 19/100
1/1 [==============================] - 0s 9ms/step - loss: 2.2987 - sparse_categorical_accuracy: 0.3636
Epoch 20/100
1/1 [==============================] - 0s 10ms/step - loss: 2.2291 - sparse_categorical_accuracy: 0.4545
Epoch 21/100
1/1 [==============================] - 0s 15ms/step - loss: 2.1612 - sparse_categorical_accuracy: 0.4545
Epoch 22/100
1/1 [==============================] - 0s 7ms/step - loss: 2.0950 - sparse_categorical_accuracy: 0.4091
Epoch 23/100
1/1 [==============================] - 0s 19ms/step - loss: 2.0304 - sparse_categorical_accuracy: 0.4545
Epoch 24/100
1/1 [==============================] - 0s 10ms/step - loss: 1.9671 - sparse_categorical_accuracy: 0.5455
Epoch 25/100
1/1 [==============================] - 0s 13ms/step - loss: 1.9046 - sparse_categorical_accuracy: 0.5455
Epoch 26/100
1/1 [==============================] - 0s 9ms/step - loss: 1.8428 - sparse_categorical_accuracy: 0.5455
Epoch 27/100
1/1 [==============================] - 0s 8ms/step - loss: 1.7819 - sparse_categorical_accuracy: 0.5909
Epoch 28/100
1/1 [==============================] - 0s 8ms/step - loss: 1.7221 - sparse_categorical_accuracy: 0.5909
Epoch 29/100
1/1 [==============================] - 0s 8ms/step - loss: 1.6639 - sparse_categorical_accuracy: 0.6818
Epoch 30/100
1/1 [==============================] - 0s 8ms/step - loss: 1.6077 - sparse_categorical_accuracy: 0.7727
Epoch 31/100
1/1 [==============================] - 0s 8ms/step - loss: 1.5537 - sparse_categorical_accuracy: 0.7727
Epoch 32/100
1/1 [==============================] - 0s 7ms/step - loss: 1.5021 - sparse_categorical_accuracy: 0.7273
Epoch 33/100
1/1 [==============================] - 0s 12ms/step - loss: 1.4527 - sparse_categorical_accuracy: 0.7273
Epoch 34/100
1/1 [==============================] - 0s 8ms/step - loss: 1.4053 - sparse_categorical_accuracy: 0.7727
Epoch 35/100
1/1 [==============================] - 0s 8ms/step - loss: 1.3595 - sparse_categorical_accuracy: 0.8182
Epoch 36/100
1/1 [==============================] - 0s 8ms/step - loss: 1.3150 - sparse_categorical_accuracy: 0.8636
Epoch 37/100
1/1 [==============================] - 0s 9ms/step - loss: 1.2715 - sparse_categorical_accuracy: 0.8636
Epoch 38/100
1/1 [==============================] - 0s 10ms/step - loss: 1.2291 - sparse_categorical_accuracy: 0.8636
Epoch 39/100
1/1 [==============================] - 0s 8ms/step - loss: 1.1876 - sparse_categorical_accuracy: 0.8636
Epoch 40/100
1/1 [==============================] - 0s 11ms/step - loss: 1.1471 - sparse_categorical_accuracy: 0.9545
Epoch 41/100
1/1 [==============================] - 0s 17ms/step - loss: 1.1075 - sparse_categorical_accuracy: 0.9545
Epoch 42/100
1/1 [==============================] - 0s 18ms/step - loss: 1.0689 - sparse_categorical_accuracy: 0.9545
Epoch 43/100
1/1 [==============================] - 0s 17ms/step - loss: 1.0310 - sparse_categorical_accuracy: 0.9545
Epoch 44/100
1/1 [==============================] - 0s 16ms/step - loss: 0.9940 - sparse_categorical_accuracy: 0.9545
Epoch 45/100
1/1 [==============================] - 0s 17ms/step - loss: 0.9578 - sparse_categorical_accuracy: 0.9545
Epoch 46/100
1/1 [==============================] - 0s 18ms/step - loss: 0.9225 - sparse_categorical_accuracy: 0.9545
Epoch 47/100
1/1 [==============================] - 0s 9ms/step - loss: 0.8883 - sparse_categorical_accuracy: 0.9545
Epoch 48/100
1/1 [==============================] - 0s 10ms/step - loss: 0.8553 - sparse_categorical_accuracy: 0.9545
Epoch 49/100
1/1 [==============================] - 0s 9ms/step - loss: 0.8237 - sparse_categorical_accuracy: 0.9545
Epoch 50/100
1/1 [==============================] - 0s 8ms/step - loss: 0.7933 - sparse_categorical_accuracy: 0.9545
Epoch 51/100
1/1 [==============================] - 0s 10ms/step - loss: 0.7641 - sparse_categorical_accuracy: 0.9545
Epoch 52/100
1/1 [==============================] - 0s 12ms/step - loss: 0.7362 - sparse_categorical_accuracy: 0.9545
Epoch 53/100
1/1 [==============================] - 0s 14ms/step - loss: 0.7096 - sparse_categorical_accuracy: 0.9545
Epoch 54/100
1/1 [==============================] - 0s 8ms/step - loss: 0.6840 - sparse_categorical_accuracy: 0.9545
Epoch 55/100
1/1 [==============================] - 0s 9ms/step - loss: 0.6594 - sparse_categorical_accuracy: 0.9545
Epoch 56/100
1/1 [==============================] - 0s 10ms/step - loss: 0.6359 - sparse_categorical_accuracy: 0.9545
Epoch 57/100
1/1 [==============================] - 0s 12ms/step - loss: 0.6132 - sparse_categorical_accuracy: 0.9545
Epoch 58/100
1/1 [==============================] - 0s 9ms/step - loss: 0.5915 - sparse_categorical_accuracy: 0.9545
Epoch 59/100
1/1 [==============================] - 0s 8ms/step - loss: 0.5705 - sparse_categorical_accuracy: 0.9545
Epoch 60/100
1/1 [==============================] - 0s 15ms/step - loss: 0.5502 - sparse_categorical_accuracy: 0.9545
Epoch 61/100
1/1 [==============================] - 0s 11ms/step - loss: 0.5307 - sparse_categorical_accuracy: 0.9545
Epoch 62/100
1/1 [==============================] - 0s 9ms/step - loss: 0.5119 - sparse_categorical_accuracy: 1.0000
Epoch 63/100
1/1 [==============================] - 0s 9ms/step - loss: 0.4939 - sparse_categorical_accuracy: 1.0000
Epoch 64/100
1/1 [==============================] - 0s 10ms/step - loss: 0.4767 - sparse_categorical_accuracy: 1.0000
Epoch 65/100
1/1 [==============================] - 0s 10ms/step - loss: 0.4602 - sparse_categorical_accuracy: 1.0000
Epoch 66/100
1/1 [==============================] - 0s 12ms/step - loss: 0.4444 - sparse_categorical_accuracy: 1.0000
Epoch 67/100
1/1 [==============================] - 0s 12ms/step - loss: 0.4293 - sparse_categorical_accuracy: 1.0000
Epoch 68/100
1/1 [==============================] - 0s 18ms/step - loss: 0.4147 - sparse_categorical_accuracy: 1.0000
Epoch 69/100
1/1 [==============================] - 0s 10ms/step - loss: 0.4007 - sparse_categorical_accuracy: 1.0000
Epoch 70/100
1/1 [==============================] - 0s 8ms/step - loss: 0.3873 - sparse_categorical_accuracy: 1.0000
Epoch 71/100
1/1 [==============================] - 0s 10ms/step - loss: 0.3745 - sparse_categorical_accuracy: 1.0000
Epoch 72/100
1/1 [==============================] - 0s 9ms/step - loss: 0.3622 - sparse_categorical_accuracy: 1.0000
Epoch 73/100
1/1 [==============================] - 0s 7ms/step - loss: 0.3505 - sparse_categorical_accuracy: 1.0000
Epoch 74/100
1/1 [==============================] - 0s 9ms/step - loss: 0.3393 - sparse_categorical_accuracy: 1.0000
Epoch 75/100
1/1 [==============================] - 0s 7ms/step - loss: 0.3285 - sparse_categorical_accuracy: 1.0000
Epoch 76/100
1/1 [==============================] - 0s 9ms/step - loss: 0.3182 - sparse_categorical_accuracy: 1.0000
Epoch 77/100
1/1 [==============================] - 0s 12ms/step - loss: 0.3083 - sparse_categorical_accuracy: 1.0000
Epoch 78/100
1/1 [==============================] - 0s 10ms/step - loss: 0.2988 - sparse_categorical_accuracy: 1.0000
Epoch 79/100
1/1 [==============================] - 0s 9ms/step - loss: 0.2898 - sparse_categorical_accuracy: 1.0000
Epoch 80/100
1/1 [==============================] - 0s 12ms/step - loss: 0.2811 - sparse_categorical_accuracy: 1.0000
Epoch 81/100
1/1 [==============================] - 0s 11ms/step - loss: 0.2728 - sparse_categorical_accuracy: 1.0000
Epoch 82/100
1/1 [==============================] - 0s 9ms/step - loss: 0.2649 - sparse_categorical_accuracy: 1.0000
Epoch 83/100
1/1 [==============================] - 0s 13ms/step - loss: 0.2572 - sparse_categorical_accuracy: 1.0000
Epoch 84/100
1/1 [==============================] - 0s 22ms/step - loss: 0.2498 - sparse_categorical_accuracy: 1.0000
Epoch 85/100
1/1 [==============================] - 0s 13ms/step - loss: 0.2428 - sparse_categorical_accuracy: 1.0000
Epoch 86/100
1/1 [==============================] - 0s 15ms/step - loss: 0.2360 - sparse_categorical_accuracy: 1.0000
Epoch 87/100
1/1 [==============================] - 0s 15ms/step - loss: 0.2295 - sparse_categorical_accuracy: 1.0000
Epoch 88/100
1/1 [==============================] - 0s 11ms/step - loss: 0.2233 - sparse_categorical_accuracy: 1.0000
Epoch 89/100
1/1 [==============================] - 0s 11ms/step - loss: 0.2173 - sparse_categorical_accuracy: 1.0000
Epoch 90/100
1/1 [==============================] - 0s 12ms/step - loss: 0.2115 - sparse_categorical_accuracy: 1.0000
Epoch 91/100
1/1 [==============================] - 0s 16ms/step - loss: 0.2060 - sparse_categorical_accuracy: 1.0000
Epoch 92/100
1/1 [==============================] - 0s 20ms/step - loss: 0.2007 - sparse_categorical_accuracy: 1.0000
Epoch 93/100
1/1 [==============================] - 0s 15ms/step - loss: 0.1956 - sparse_categorical_accuracy: 1.0000
Epoch 94/100
1/1 [==============================] - 0s 15ms/step - loss: 0.1907 - sparse_categorical_accuracy: 1.0000
Epoch 95/100
1/1 [==============================] - 0s 18ms/step - loss: 0.1859 - sparse_categorical_accuracy: 1.0000
Epoch 96/100
1/1 [==============================] - 0s 15ms/step - loss: 0.1814 - sparse_categorical_accuracy: 1.0000
Epoch 97/100
1/1 [==============================] - 0s 17ms/step - loss: 0.1770 - sparse_categorical_accuracy: 1.0000
Epoch 98/100
1/1 [==============================] - 0s 13ms/step - loss: 0.1728 - sparse_categorical_accuracy: 1.0000
Epoch 99/100
1/1 [==============================] - 0s 10ms/step - loss: 0.1687 - sparse_categorical_accuracy: 1.0000
Epoch 100/100
1/1 [==============================] - 0s 16ms/step - loss: 0.1648 - sparse_categorical_accuracy: 1.0000
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
embedding (Embedding) (None, None, 2) 52
_________________________________________________________________
simple_rnn (SimpleRNN) (None, 10) 130
_________________________________________________________________
dense (Dense) (None, 26) 286
=================================================================
Total params: 468
Trainable params: 468
Non-trainable params: 0
_________________________________________________________________
模型结果可视化
acc = history.history['sparse_categorical_accuracy']
loss = history.history['loss']
plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.title('Training Accuracy')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.title('Training Loss')
plt.legend()
plt.show()

preNum = int(input("input the number of test alphabet:"))
for i in range(preNum):
alphabet1 = input("input test alphabet:")
alphabet = [w_to_id[a] for a in alphabet1]
# 使alphabet符合Embedding输入要求:[送入样本数, 时间展开步数]。
# 此处验证效果送入了1个样本,送入样本数为1;输入4个字母出结果,循环核时间展开步数为4。
alphabet = np.reshape(alphabet, (1, 4))
result = model.predict([alphabet])
pred = tf.argmax(result, axis=1)
pred = int(pred)
tf.print(alphabet1 + '->' + input_word[pred])
input the number of test alphabet:5
input test alphabet:abcd
abcd->e
input test alphabet:defg
defg->h
input test alphabet:asdf
asdf->f
input test alphabet:dsew
dsew->h
input test alphabet:fdfw
fdfw->f
用RNN实现股票预测
pip install tushare
Collecting tushare
Downloading tushare-1.2.64-py3-none-any.whl (214 kB)
[K |████████████████████████████████| 214 kB 8.3 MB/s
[?25hCollecting websocket-client>=0.57.0
Downloading websocket_client-1.1.0-py2.py3-none-any.whl (68 kB)
[K |████████████████████████████████| 68 kB 7.6 MB/s
[?25hCollecting simplejson>=3.16.0
Downloading simplejson-3.17.3-cp37-cp37m-manylinux_2_5_x86_64.manylinux1_x86_64.manylinux_2_12_x86_64.manylinux2010_x86_64.whl (129 kB)
[K |████████████████████████████████| 129 kB 13.7 MB/s
[?25hRequirement already satisfied: requests>=2.0.0 in /usr/local/lib/python3.7/dist-packages (from tushare) (2.23.0)
Requirement already satisfied: lxml>=3.8.0 in /usr/local/lib/python3.7/dist-packages (from tushare) (4.2.6)
Requirement already satisfied: bs4>=0.0.1 in /usr/local/lib/python3.7/dist-packages (from tushare) (0.0.1)
Requirement already satisfied: beautifulsoup4 in /usr/local/lib/python3.7/dist-packages (from bs4>=0.0.1->tushare) (4.6.3)
Requirement already satisfied: chardet<4,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from requests>=2.0.0->tushare) (3.0.4)
Requirement already satisfied: certifi>=2017.4.17 in /usr/local/lib/python3.7/dist-packages (from requests>=2.0.0->tushare) (2021.5.30)
Requirement already satisfied: idna<3,>=2.5 in /usr/local/lib/python3.7/dist-packages (from requests>=2.0.0->tushare) (2.10)
Requirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in /usr/local/lib/python3.7/dist-packages (from requests>=2.0.0->tushare) (1.24.3)
Installing collected packages: websocket-client, simplejson, tushare
Successfully installed simplejson-3.17.3 tushare-1.2.64 websocket-client-1.1.0
import tushare as ts
import matplotlib.pyplot as plt
df1 = ts.get_k_data('600519', ktype='D', start='2010-06-22', end='2020-06-22')
datapath1 = "./BSH600519.csv"
df1.to_csv(datapath1)
本接口即将停止更新,请尽快使用Pro版接口:https://waditu.com/document/2
读取股票文件
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dropout, Dense, SimpleRNN
import matplotlib.pyplot as plt
import os
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
maotai = pd.read_csv('./BSH600519.csv') # 读取股票文件
maotai.head()
| Unnamed: 0 | date | open | close | high | low | volume | code | |
|---|---|---|---|---|---|---|---|---|
| 0 | 109 | 2010-06-22 | 85.039 | 84.356 | 85.473 | 83.852 | 20779.10 | 600519 |
| 1 | 110 | 2010-06-23 | 84.235 | 84.043 | 84.796 | 83.865 | 12812.76 | 600519 |
| 2 | 111 | 2010-06-24 | 84.177 | 82.939 | 84.535 | 82.754 | 24344.03 | 600519 |
| 3 | 112 | 2010-06-25 | 82.831 | 83.290 | 83.597 | 82.212 | 19011.35 | 600519 |
| 4 | 113 | 2010-06-28 | 83.086 | 81.689 | 83.099 | 81.561 | 14816.98 | 600519 |
划分训练集与测试集
training_set = maotai.iloc[0:2426 - 300, 2:3].values # 前(2426-300=2126)天的开盘价作为训练集,表格从0开始计数,2:3 是提取[2:3)列,前闭后开,故提取出C列开盘价
test_set = maotai.iloc[2426 - 300:, 2:3].values # 后300天的开盘价作为测试集
training_set
array([[ 85.039],
[ 84.235],
[ 84.177],
...,
[788. ],
[788.22 ],
[786. ]])
test_set.shape
(303, 1)
归一化
sc=MinMaxScaler(feature_range=(0,1))
training_set_scaled=sc.fit_transform(training_set)
test_set=sc.fit_transform(test_set)
x_train = []
y_train = []
x_test = []
y_test = []
x_test[0]
array([[0. ],
[0.00152648],
[0.02050069],
[0.08395665],
[0.12211876],
[0.1221035 ],
[0.09177225],
[0.09158907],
[0.18317814],
[0.18775759],
[0.18775759],
[0.2564494 ],
[0.1969165 ],
[0.23049916],
[0.19065791],
[0.24118455],
[0.2524958 ],
[0.2502824 ],
[0.27400397],
[0.26102885],
[0.30511372],
[0.28818501],
[0.25385437],
[0.25186994],
[0.28697909],
[0.2221035 ],
[0.17292016],
[0.12211876],
[0.14501603],
[0.14602351],
[0.18143795],
[0.16028087],
[0.16827965],
[0.21218135],
[0.22442375],
[0.18317814],
[0.16028087],
[0.17551519],
[0.15417494],
[0.12975118],
[0.15127461],
[0.14958022],
[0.16487559],
[0.19844299],
[0.18398718],
[0.17096626],
[0.17554572],
[0.15875439],
[0.14596245],
[0.11903526],
[0.14654251],
[0.19267287],
[0.19844299],
[0.19996947],
[0.19386353],
[0.20912838],
[0.24423752],
[0.23278889],
[0.28998626],
[0.30270188]])
model = tf.keras.Sequential([
SimpleRNN(80, return_sequences=True),
Dropout(0.2),
SimpleRNN(100),
Dropout(0.2),
Dense(1)
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss='mean_squared_error') # 损失函数用均方误差
# 该应用只观测loss数值,不观测准确率,所以删去metrics选项,一会在每个epoch迭代显示时只显示loss值
history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test))
Epoch 1/50
33/33 [==============================] - 4s 96ms/step - loss: 0.1104 - val_loss: 0.0105
Epoch 2/50
33/33 [==============================] - 3s 92ms/step - loss: 0.0264 - val_loss: 0.0259
Epoch 3/50
33/33 [==============================] - 3s 92ms/step - loss: 0.0155 - val_loss: 0.0063
Epoch 4/50
33/33 [==============================] - 3s 90ms/step - loss: 0.0125 - val_loss: 0.0043
Epoch 5/50
33/33 [==============================] - 3s 91ms/step - loss: 0.0086 - val_loss: 0.0042
Epoch 6/50
33/33 [==============================] - 3s 94ms/step - loss: 0.0077 - val_loss: 0.0069
Epoch 7/50
33/33 [==============================] - 3s 90ms/step - loss: 0.0066 - val_loss: 0.0036
Epoch 8/50
33/33 [==============================] - 3s 91ms/step - loss: 0.0061 - val_loss: 0.0071
Epoch 9/50
33/33 [==============================] - 3s 89ms/step - loss: 0.0052 - val_loss: 0.0025
Epoch 10/50
33/33 [==============================] - 3s 91ms/step - loss: 0.0052 - val_loss: 0.0024
Epoch 11/50
33/33 [==============================] - 3s 92ms/step - loss: 0.0039 - val_loss: 0.0022
Epoch 12/50
33/33 [==============================] - 3s 86ms/step - loss: 0.0041 - val_loss: 0.0021
Epoch 13/50
33/33 [==============================] - 3s 86ms/step - loss: 0.0043 - val_loss: 0.0020
Epoch 14/50
33/33 [==============================] - 3s 87ms/step - loss: 0.0037 - val_loss: 0.0018
Epoch 15/50
33/33 [==============================] - 3s 91ms/step - loss: 0.0031 - val_loss: 0.0026
Epoch 16/50
33/33 [==============================] - 3s 91ms/step - loss: 0.0030 - val_loss: 0.0020
Epoch 17/50
33/33 [==============================] - 3s 90ms/step - loss: 0.0031 - val_loss: 0.0018
Epoch 18/50
33/33 [==============================] - 3s 88ms/step - loss: 0.0030 - val_loss: 0.0022
Epoch 19/50
33/33 [==============================] - 3s 88ms/step - loss: 0.0027 - val_loss: 0.0016
Epoch 20/50
33/33 [==============================] - 3s 85ms/step - loss: 0.0026 - val_loss: 0.0022
Epoch 21/50
33/33 [==============================] - 3s 87ms/step - loss: 0.0026 - val_loss: 0.0014
Epoch 22/50
33/33 [==============================] - 3s 87ms/step - loss: 0.0025 - val_loss: 0.0018
Epoch 23/50
33/33 [==============================] - 3s 86ms/step - loss: 0.0020 - val_loss: 0.0015
Epoch 24/50
33/33 [==============================] - 3s 91ms/step - loss: 0.0024 - val_loss: 0.0020
Epoch 25/50
33/33 [==============================] - 3s 91ms/step - loss: 0.0022 - val_loss: 0.0014
Epoch 26/50
33/33 [==============================] - 3s 94ms/step - loss: 0.0019 - val_loss: 0.0013
Epoch 27/50
33/33 [==============================] - 3s 93ms/step - loss: 0.0019 - val_loss: 0.0013
Epoch 28/50
33/33 [==============================] - 3s 94ms/step - loss: 0.0021 - val_loss: 0.0015
Epoch 29/50
33/33 [==============================] - 3s 94ms/step - loss: 0.0019 - val_loss: 0.0013
Epoch 30/50
33/33 [==============================] - 3s 90ms/step - loss: 0.0018 - val_loss: 0.0013
Epoch 31/50
33/33 [==============================] - 3s 100ms/step - loss: 0.0017 - val_loss: 0.0018
Epoch 32/50
33/33 [==============================] - 3s 96ms/step - loss: 0.0018 - val_loss: 0.0012
Epoch 33/50
33/33 [==============================] - 3s 87ms/step - loss: 0.0016 - val_loss: 0.0013
Epoch 34/50
33/33 [==============================] - 3s 87ms/step - loss: 0.0014 - val_loss: 0.0014
Epoch 35/50
33/33 [==============================] - 3s 91ms/step - loss: 0.0017 - val_loss: 0.0013
Epoch 36/50
33/33 [==============================] - 3s 86ms/step - loss: 0.0016 - val_loss: 0.0015
Epoch 37/50
33/33 [==============================] - 3s 86ms/step - loss: 0.0017 - val_loss: 0.0016
Epoch 38/50
33/33 [==============================] - 3s 86ms/step - loss: 0.0014 - val_loss: 0.0012
Epoch 39/50
33/33 [==============================] - 3s 84ms/step - loss: 0.0015 - val_loss: 0.0012
Epoch 40/50
33/33 [==============================] - 3s 87ms/step - loss: 0.0013 - val_loss: 0.0013
Epoch 41/50
33/33 [==============================] - 3s 85ms/step - loss: 0.0013 - val_loss: 0.0013
Epoch 42/50
33/33 [==============================] - 3s 94ms/step - loss: 0.0015 - val_loss: 0.0012
Epoch 43/50
33/33 [==============================] - 3s 91ms/step - loss: 0.0014 - val_loss: 0.0012
Epoch 44/50
33/33 [==============================] - 3s 90ms/step - loss: 0.0015 - val_loss: 0.0013
Epoch 45/50
33/33 [==============================] - 3s 90ms/step - loss: 0.0014 - val_loss: 0.0014
Epoch 46/50
33/33 [==============================] - 3s 88ms/step - loss: 0.0013 - val_loss: 0.0012
Epoch 47/50
33/33 [==============================] - 3s 93ms/step - loss: 0.0012 - val_loss: 0.0011
Epoch 48/50
33/33 [==============================] - 3s 95ms/step - loss: 0.0014 - val_loss: 0.0020
Epoch 49/50
33/33 [==============================] - 3s 95ms/step - loss: 0.0012 - val_loss: 0.0011
Epoch 50/50
33/33 [==============================] - 3s 93ms/step - loss: 0.0012 - val_loss: 0.0012
model.summary()
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
simple_rnn_5 (SimpleRNN) (None, 60, 80) 6560
_________________________________________________________________
dropout_4 (Dropout) (None, 60, 80) 0
_________________________________________________________________
simple_rnn_6 (SimpleRNN) (None, 100) 18100
_________________________________________________________________
dropout_5 (Dropout) (None, 100) 0
_________________________________________________________________
dense_3 (Dense) (None, 1) 101
=================================================================
Total params: 24,761
Trainable params: 24,761
Non-trainable params: 0
_________________________________________________________________
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()

predicted_stock_price = model.predict(x_test)
# 对预测数据还原---从(0,1)反归一化到原始范围
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
# 对真实数据还原---从(0,1)反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='MaoTai Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted MaoTai Stock Price')
plt.title('MaoTai Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('MaoTai Stock Price')
plt.legend()
plt.show()
mse = mean_squared_error(predicted_stock_price, real_stock_price)
# calculate RMSE 均方根误差--->sqrt[MSE] (对均方误差开方)
rmse = math.sqrt(mean_squared_error(predicted_stock_price, real_stock_price))
# calculate MAE 平均绝对误差----->E[|预测值-真实值|](预测值减真实值求绝对值后求均值)
mae = mean_absolute_error(predicted_stock_price, real_stock_price)
print('均方误差: %.6f' % mse)
print('均方根误差: %.6f' % rmse)
print('平均绝对误差: %.6f' % mae)

均方误差: 494.772715
均方根误差: 22.243487
平均绝对误差: 16.893783
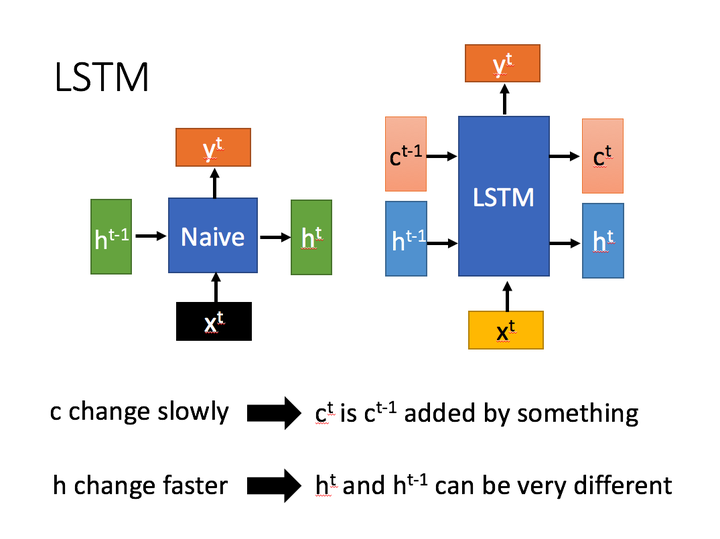
https://zhuanlan.zhihu.com/p/32085405
# 用LSTM实现股票预测
# 传统的RNN网络可以通过记忆体实现短期记忆,进行连续数据的预测,但是当连续数据过长时,会使展开的时间步过长,在反向传播更新参数时,梯度要按时间步连续相乘会导致梯度消失。
from tensorflow.keras.layers import Dropout, Dense, LSTM
model = tf.keras.Sequential([
LSTM(80, return_sequences=True),
Dropout(0.2),
LSTM(100),
Dropout(0.2),
Dense(1)
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss='mean_squared_error')
history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test), validation_freq=1,
)
Epoch 1/50
33/33 [==============================] - 7s 29ms/step - loss: 0.0186 - val_loss: 0.0085
Epoch 2/50
33/33 [==============================] - 0s 10ms/step - loss: 0.0016 - val_loss: 0.0044
Epoch 3/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0012 - val_loss: 0.0049
Epoch 4/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0013 - val_loss: 0.0043
Epoch 5/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0011 - val_loss: 0.0041
Epoch 6/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0011 - val_loss: 0.0039
Epoch 7/50
33/33 [==============================] - 0s 10ms/step - loss: 0.0011 - val_loss: 0.0039
Epoch 8/50
33/33 [==============================] - 0s 9ms/step - loss: 9.5742e-04 - val_loss: 0.0044
Epoch 9/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0010 - val_loss: 0.0038
Epoch 10/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0011 - val_loss: 0.0038
Epoch 11/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0011 - val_loss: 0.0036
Epoch 12/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0012 - val_loss: 0.0037
Epoch 13/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0012 - val_loss: 0.0037
Epoch 14/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0010 - val_loss: 0.0035
Epoch 15/50
33/33 [==============================] - 0s 9ms/step - loss: 9.8173e-04 - val_loss: 0.0038
Epoch 16/50
33/33 [==============================] - 0s 9ms/step - loss: 9.8285e-04 - val_loss: 0.0036
Epoch 17/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0011 - val_loss: 0.0034
Epoch 18/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0011 - val_loss: 0.0035
Epoch 19/50
33/33 [==============================] - 0s 9ms/step - loss: 9.6086e-04 - val_loss: 0.0032
Epoch 20/50
33/33 [==============================] - 0s 9ms/step - loss: 9.6718e-04 - val_loss: 0.0032
Epoch 21/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0013 - val_loss: 0.0032
Epoch 22/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0010 - val_loss: 0.0032
Epoch 23/50
33/33 [==============================] - 0s 9ms/step - loss: 9.2470e-04 - val_loss: 0.0033
Epoch 24/50
33/33 [==============================] - 0s 9ms/step - loss: 8.9740e-04 - val_loss: 0.0039
Epoch 25/50
33/33 [==============================] - 0s 9ms/step - loss: 9.1009e-04 - val_loss: 0.0039
Epoch 26/50
33/33 [==============================] - 0s 9ms/step - loss: 8.7304e-04 - val_loss: 0.0029
Epoch 27/50
33/33 [==============================] - 0s 9ms/step - loss: 9.7182e-04 - val_loss: 0.0036
Epoch 28/50
33/33 [==============================] - 0s 9ms/step - loss: 8.6223e-04 - val_loss: 0.0030
Epoch 29/50
33/33 [==============================] - 0s 10ms/step - loss: 8.3734e-04 - val_loss: 0.0030
Epoch 30/50
33/33 [==============================] - 0s 10ms/step - loss: 8.3925e-04 - val_loss: 0.0036
Epoch 31/50
33/33 [==============================] - 0s 9ms/step - loss: 8.1819e-04 - val_loss: 0.0028
Epoch 32/50
33/33 [==============================] - 0s 9ms/step - loss: 7.6080e-04 - val_loss: 0.0028
Epoch 33/50
33/33 [==============================] - 0s 9ms/step - loss: 6.7988e-04 - val_loss: 0.0029
Epoch 34/50
33/33 [==============================] - 0s 9ms/step - loss: 7.7297e-04 - val_loss: 0.0027
Epoch 35/50
33/33 [==============================] - 0s 9ms/step - loss: 8.6007e-04 - val_loss: 0.0027
Epoch 36/50
33/33 [==============================] - 0s 9ms/step - loss: 7.1354e-04 - val_loss: 0.0026
Epoch 37/50
33/33 [==============================] - 0s 9ms/step - loss: 7.9805e-04 - val_loss: 0.0028
Epoch 38/50
33/33 [==============================] - 0s 9ms/step - loss: 7.4727e-04 - val_loss: 0.0026
Epoch 39/50
33/33 [==============================] - 0s 10ms/step - loss: 7.5746e-04 - val_loss: 0.0036
Epoch 40/50
33/33 [==============================] - 0s 9ms/step - loss: 8.6356e-04 - val_loss: 0.0030
Epoch 41/50
33/33 [==============================] - 0s 9ms/step - loss: 6.8185e-04 - val_loss: 0.0025
Epoch 42/50
33/33 [==============================] - 0s 11ms/step - loss: 7.8925e-04 - val_loss: 0.0025
Epoch 43/50
33/33 [==============================] - 0s 10ms/step - loss: 6.6461e-04 - val_loss: 0.0025
Epoch 44/50
33/33 [==============================] - 0s 9ms/step - loss: 8.1635e-04 - val_loss: 0.0027
Epoch 45/50
33/33 [==============================] - 0s 9ms/step - loss: 7.7723e-04 - val_loss: 0.0025
Epoch 46/50
33/33 [==============================] - 0s 10ms/step - loss: 7.4206e-04 - val_loss: 0.0027
Epoch 47/50
33/33 [==============================] - 0s 9ms/step - loss: 6.8740e-04 - val_loss: 0.0037
Epoch 48/50
33/33 [==============================] - 0s 9ms/step - loss: 8.9900e-04 - val_loss: 0.0024
Epoch 49/50
33/33 [==============================] - 0s 9ms/step - loss: 7.5526e-04 - val_loss: 0.0025
Epoch 50/50
33/33 [==============================] - 0s 9ms/step - loss: 6.8012e-04 - val_loss: 0.0024
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()
################## predict ######################
# 测试集输入模型进行预测
predicted_stock_price = model.predict(x_test)
# 对预测数据还原---从(0,1)反归一化到原始范围
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
# 对真实数据还原---从(0,1)反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='MaoTai Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted MaoTai Stock Price')
plt.title('MaoTai Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('MaoTai Stock Price')
plt.legend()
plt.show()
##########evaluate##############
# calculate MSE 均方误差 ---> E[(预测值-真实值)^2] (预测值减真实值求平方后求均值)
mse = mean_squared_error(predicted_stock_price, real_stock_price)
# calculate RMSE 均方根误差--->sqrt[MSE] (对均方误差开方)
rmse = math.sqrt(mean_squared_error(predicted_stock_price, real_stock_price))
# calculate MAE 平均绝对误差----->E[|预测值-真实值|](预测值减真实值求绝对值后求均值)
mae = mean_absolute_error(predicted_stock_price, real_stock_price)
print('均方误差: %.6f' % mse)
print('均方根误差: %.6f' % rmse)
print('平均绝对误差: %.6f' % mae)


均方误差: 1046.218086
均方根误差: 32.345295
平均绝对误差: 25.770339
# 用GRU实现股票预测
from tensorflow.keras.layers import Dropout, Dense, GRU
model = tf.keras.Sequential([
GRU(80, return_sequences=True),
Dropout(0.2),
GRU(100),
Dropout(0.2),
Dense(1)
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss='mean_squared_error')
history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test), validation_freq=1,
)
Epoch 1/50
33/33 [==============================] - 4s 28ms/step - loss: 0.0215 - val_loss: 0.0044
Epoch 2/50
33/33 [==============================] - 0s 10ms/step - loss: 0.0017 - val_loss: 0.0021
Epoch 3/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0012 - val_loss: 0.0021
Epoch 4/50
33/33 [==============================] - 0s 9ms/step - loss: 0.0011 - val_loss: 0.0017
Epoch 5/50
33/33 [==============================] - 0s 9ms/step - loss: 9.3049e-04 - val_loss: 0.0017
Epoch 6/50
33/33 [==============================] - 0s 9ms/step - loss: 9.9081e-04 - val_loss: 0.0017
Epoch 7/50
33/33 [==============================] - 0s 9ms/step - loss: 8.6785e-04 - val_loss: 0.0017
Epoch 8/50
33/33 [==============================] - 0s 9ms/step - loss: 8.3467e-04 - val_loss: 0.0021
Epoch 9/50
33/33 [==============================] - 0s 9ms/step - loss: 9.4968e-04 - val_loss: 0.0016
Epoch 10/50
33/33 [==============================] - 0s 9ms/step - loss: 8.0756e-04 - val_loss: 0.0017
Epoch 11/50
33/33 [==============================] - 0s 9ms/step - loss: 8.5001e-04 - val_loss: 0.0016
Epoch 12/50
33/33 [==============================] - 0s 8ms/step - loss: 0.0010 - val_loss: 0.0017
Epoch 13/50
33/33 [==============================] - 0s 9ms/step - loss: 8.7025e-04 - val_loss: 0.0016
Epoch 14/50
33/33 [==============================] - 0s 9ms/step - loss: 7.5788e-04 - val_loss: 0.0016
Epoch 15/50
33/33 [==============================] - 0s 9ms/step - loss: 8.2795e-04 - val_loss: 0.0017
Epoch 16/50
33/33 [==============================] - 0s 9ms/step - loss: 7.7878e-04 - val_loss: 0.0016
Epoch 17/50
33/33 [==============================] - 0s 9ms/step - loss: 7.9201e-04 - val_loss: 0.0019
Epoch 18/50
33/33 [==============================] - 0s 9ms/step - loss: 8.2570e-04 - val_loss: 0.0017
Epoch 19/50
33/33 [==============================] - 0s 9ms/step - loss: 7.4630e-04 - val_loss: 0.0015
Epoch 20/50
33/33 [==============================] - 0s 9ms/step - loss: 7.2326e-04 - val_loss: 0.0016
Epoch 21/50
33/33 [==============================] - 0s 9ms/step - loss: 9.1477e-04 - val_loss: 0.0015
Epoch 22/50
33/33 [==============================] - 0s 9ms/step - loss: 6.9578e-04 - val_loss: 0.0015
Epoch 23/50
33/33 [==============================] - 0s 9ms/step - loss: 7.0172e-04 - val_loss: 0.0016
Epoch 24/50
33/33 [==============================] - 0s 9ms/step - loss: 6.8265e-04 - val_loss: 0.0018
Epoch 25/50
33/33 [==============================] - 0s 10ms/step - loss: 7.3948e-04 - val_loss: 0.0024
Epoch 26/50
33/33 [==============================] - 0s 9ms/step - loss: 7.1338e-04 - val_loss: 0.0015
Epoch 27/50
33/33 [==============================] - 0s 9ms/step - loss: 7.1968e-04 - val_loss: 0.0015
Epoch 28/50
33/33 [==============================] - 0s 9ms/step - loss: 7.2262e-04 - val_loss: 0.0014
Epoch 29/50
33/33 [==============================] - 0s 8ms/step - loss: 6.7821e-04 - val_loss: 0.0014
Epoch 30/50
33/33 [==============================] - 0s 8ms/step - loss: 6.4962e-04 - val_loss: 0.0018
Epoch 31/50
33/33 [==============================] - 0s 8ms/step - loss: 6.8530e-04 - val_loss: 0.0014
Epoch 32/50
33/33 [==============================] - 0s 9ms/step - loss: 6.5112e-04 - val_loss: 0.0015
Epoch 33/50
33/33 [==============================] - 0s 8ms/step - loss: 5.4305e-04 - val_loss: 0.0020
Epoch 34/50
33/33 [==============================] - 0s 8ms/step - loss: 6.6791e-04 - val_loss: 0.0014
Epoch 35/50
33/33 [==============================] - 0s 8ms/step - loss: 7.0010e-04 - val_loss: 0.0017
Epoch 36/50
33/33 [==============================] - 0s 8ms/step - loss: 5.9378e-04 - val_loss: 0.0014
Epoch 37/50
33/33 [==============================] - 0s 8ms/step - loss: 6.6852e-04 - val_loss: 0.0016
Epoch 38/50
33/33 [==============================] - 0s 8ms/step - loss: 6.4256e-04 - val_loss: 0.0014
Epoch 39/50
33/33 [==============================] - 0s 8ms/step - loss: 6.8688e-04 - val_loss: 0.0030
Epoch 40/50
33/33 [==============================] - 0s 8ms/step - loss: 7.1045e-04 - val_loss: 0.0013
Epoch 41/50
33/33 [==============================] - 0s 8ms/step - loss: 6.5126e-04 - val_loss: 0.0013
Epoch 42/50
33/33 [==============================] - 0s 9ms/step - loss: 6.2815e-04 - val_loss: 0.0013
Epoch 43/50
33/33 [==============================] - 0s 8ms/step - loss: 5.6943e-04 - val_loss: 0.0013
Epoch 44/50
33/33 [==============================] - 0s 8ms/step - loss: 6.7888e-04 - val_loss: 0.0013
Epoch 45/50
33/33 [==============================] - 0s 8ms/step - loss: 6.1968e-04 - val_loss: 0.0013
Epoch 46/50
33/33 [==============================] - 0s 8ms/step - loss: 5.4166e-04 - val_loss: 0.0015
Epoch 47/50
33/33 [==============================] - 0s 8ms/step - loss: 5.6479e-04 - val_loss: 0.0019
Epoch 48/50
33/33 [==============================] - 0s 8ms/step - loss: 7.7698e-04 - val_loss: 0.0013
Epoch 49/50
33/33 [==============================] - 0s 8ms/step - loss: 6.2345e-04 - val_loss: 0.0013
Epoch 50/50
33/33 [==============================] - 0s 8ms/step - loss: 5.5486e-04 - val_loss: 0.0015
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()
################## predict ######################
# 测试集输入模型进行预测
predicted_stock_price = model.predict(x_test)
# 对预测数据还原---从(0,1)反归一化到原始范围
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
# 对真实数据还原---从(0,1)反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='MaoTai Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted MaoTai Stock Price')
plt.title('MaoTai Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('MaoTai Stock Price')
plt.legend()
plt.show()
##########evaluate##############
# calculate MSE 均方误差 ---> E[(预测值-真实值)^2] (预测值减真实值求平方后求均值)
mse = mean_squared_error(predicted_stock_price, real_stock_price)
# calculate RMSE 均方根误差--->sqrt[MSE] (对均方误差开方)
rmse = math.sqrt(mean_squared_error(predicted_stock_price, real_stock_price))
# calculate MAE 平均绝对误差----->E[|预测值-真实值|](预测值减真实值求绝对值后求均值)
mae = mean_absolute_error(predicted_stock_price, real_stock_price)
print('均方误差: %.6f' % mse)
print('均方根误差: %.6f' % rmse)
print('平均绝对误差: %.6f' % mae)


均方误差: 658.577031
均方根误差: 25.662756
平均绝对误差: 20.267645
maotai = pd.read_csv('./BSH600519.csv') # 读取股票文件
maotai.head()
| Unnamed: 0 | date | open | close | high | low | volume | code | |
|---|---|---|---|---|---|---|---|---|
| 0 | 109 | 2010-06-22 | 85.039 | 84.356 | 85.473 | 83.852 | 20779.10 | 600519 |
| 1 | 110 | 2010-06-23 | 84.235 | 84.043 | 84.796 | 83.865 | 12812.76 | 600519 |
| 2 | 111 | 2010-06-24 | 84.177 | 82.939 | 84.535 | 82.754 | 24344.03 | 600519 |
| 3 | 112 | 2010-06-25 | 82.831 | 83.290 | 83.597 | 82.212 | 19011.35 | 600519 |
| 4 | 113 | 2010-06-28 | 83.086 | 81.689 | 83.099 | 81.561 | 14816.98 | 600519 |
df1=maotai.iloc[:,2:7]
df1.head()
| open | close | high | low | volume | |
|---|---|---|---|---|---|
| 0 | 85.039 | 84.356 | 85.473 | 83.852 | 20779.10 |
| 1 | 84.235 | 84.043 | 84.796 | 83.865 | 12812.76 |
| 2 | 84.177 | 82.939 | 84.535 | 82.754 | 24344.03 |
| 3 | 82.831 | 83.290 | 83.597 | 82.212 | 19011.35 |
| 4 | 83.086 | 81.689 | 83.099 | 81.561 | 14816.98 |
# 归一化
from sklearn import preprocessing#进行归一化操作
min_max_scaler = preprocessing.MinMaxScaler()
df0=min_max_scaler.fit_transform(df1)
df = pd.DataFrame(df0, columns=df1.columns)
df.tail()
| open | close | high | low | volume | |
|---|---|---|---|---|---|
| 2424 | 0.972983 | 0.973544 | 0.977123 | 0.970387 | 0.077273 |
| 2425 | 0.982845 | 0.974368 | 0.975584 | 0.971783 | 0.042648 |
| 2426 | 0.977707 | 0.980254 | 0.976537 | 0.975538 | 0.048175 |
| 2427 | 0.988854 | 1.000000 | 1.000000 | 0.986623 | 0.111888 |
| 2428 | 1.000000 | 0.999382 | 0.999039 | 1.000000 | 0.056116 |
# 排序
order=["open","high","low","volume","close"]
df=df[order]
df.tail()
| open | high | low | volume | close | |
|---|---|---|---|---|---|
| 2424 | 0.972983 | 0.977123 | 0.970387 | 0.077273 | 0.973544 |
| 2425 | 0.982845 | 0.975584 | 0.971783 | 0.042648 | 0.974368 |
| 2426 | 0.977707 | 0.976537 | 0.975538 | 0.048175 | 0.980254 |
| 2427 | 0.988854 | 1.000000 | 0.986623 | 0.111888 | 1.000000 |
| 2428 | 1.000000 | 0.999039 | 1.000000 | 0.056116 | 0.999382 |
# 划分训练集,测试集
feanum=10#一共有多少特征
window=5#时间窗设置
stock=df
seq_len=window
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn import preprocessing
from sklearn.metrics import mean_squared_error
from math import sqrt
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.layers.recurrent import LSTM
amount_of_features
5
amount_of_features = len(stock.columns)#有几列
data = stock.values #pd.DataFrame(stock) 表格转化为矩阵
sequence_length = seq_len + 1#序列长度+1
result=[]
for index in range(len(data) - sequence_length):
result.append(data[index: index + sequence_length])
result = np.array(result)
result.shape
(2423, 6, 5)
cut=10#分训练集测试集 最后cut个样本为测试集
train = result[:-cut, :]
x_train = train[:, :-1]
y_train = train[:, -1][:,-1]
x_test = result[-cut:, :-1]
y_test = result[-cut:, -1][:,-1]
x_train.shape
(2413, 5, 5)
x_train
X_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], amount_of_features))
X_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], amount_of_features))
d = 0.0001
model = Sequential()#建立层次模型
model.add(LSTM(64, input_shape=(window, feanum), return_sequences=True))#建立LSTM层
model.add(Dropout(d))#建立的遗忘层
model.add(LSTM(16, input_shape=(window, feanum), return_sequences=False))#建立LSTM层
model.add(Dropout(d))#建立的遗忘层
model.add(Dense(4,activation='relu')) #建立全连接层
model.add(Dense(1,activation='relu'))
model.compile(loss='mse',optimizer='adam',metrics=['accuracy'])


 浙公网安备 33010602011771号
浙公网安备 33010602011771号