神经网络损失函数的理解

损失函数

目录

⭕返回主目录

1. 问题
2. 似然估计
3. 交叉熵损失

问题

在minibackward中我们知道了神经网络的梯度是如何反向传播的，之前一直有一个疑问也在这里得到了解答

就是求损失的时候将批量中的损失相加(或平均)与单独求每个损失相比有没有区别

• 相加操作在反向传播的时候是把梯度分配给每一项，结果是什么并不重要，因此是否相加求和，反向传播时起始梯度都是1
• 求均值只不过是在相加的基础上多了除法，结果也就是对起始梯度进行缩放，最终梯度会成比例减小，因此也没有影响

---

理解

最小二乘法

很直观不再赘述

似然估计

似然估计是给定现实世界的数据观测来评估不同模型的概率的方法
以抛硬币为例模型甲说正面概率为0.7，反面概率为0.3，模型乙说正面概率为0.5，反面概率为0.5，现实中我们抛出5个硬币其中3个正面两个反面，如何断定两个模型的好与坏呢？
首先，现实中得出的结果（实际应该很多）最能反映出正确模型的分布，因为是从正确模型中采样得到，因此应该以现实观测为基准计算在两个不同的模型下出现观测结果的概率是多少，很简单抛硬币是独立同分布的

\[P_甲 = 0.7^3 \times 0.3^2 = 0.03087 \]

\[P_乙 = 0.7^3 \times 0.3^2 = 0.03125 \]

显然计算得到乙的结果更好

---

因此我们就可以推出到神经网络做二分类时的损失函数可以怎么设计了

假设让神经网络判断一张图片是不是猫，那么在softmax的处理下神将网络的输出值就可以看作是是猫和不是猫的概率，因此给我一个批次的输入值，其标签分别是（x1，x2，x3）那么就可以根据模型给出的结果来判断这个模型是一个正确模型的概率，假设模型分别给出是猫的概率为（y1，y2，y3）自然地，经softmax后不是猫的概率为（1-y）,因此

\[P = \prod_{i=1}^{3} y_i^{x_i}(1-y_i)^{1-x_i} \]

其中x=1是猫，x=0不是猫，这种形式的连乘很难求导并且值也很小，因此整体进行log（单调），

\[\log_{}{(P)} = \sum_{i=1}^3 x_i\log(y_i) + (1-x_i)\log(1-y_i) \]

因此\(log(P)\)越大表示模型越精确，在神经网络中可以

\[Loss = -\log(P) \]

因此损失越小模型也就越精确

🔼返回顶部

---

交叉熵损失

要了解交叉熵损失首先要看什么是熵，而熵被定义为信息量的期望，我们得知道什么是信息量

信息量：先来看一个例子，假设你是旅行者，有四扇门A，B，C，D其中一个门后面有宝箱，起初时你什么也不知道，开一扇门有宝箱的概率是\(\frac{1}{4}\)，现在我告诉你A，B后面没有宝箱，现在你开出宝箱的概率是\(\frac{1}{2}\)，然后又告诉你C后面没有宝箱，现在你开出宝箱的概率是1。
你开始时越不确定后来获得的信息量就越大
其次，分两步告诉你，和一次性告诉你所含的信息量应该一样多，开始时有\(\frac{1}{2}\)概率在C，D门，我们告诉你不在A，B门，这条消息的信息量我们记为\(f(\frac{1}{2})\)，因为我们将不确定性从\(\frac{1}{4}\)降到了\(\frac{1}{2}\)，同理告诉你不在C门，这条消息的信息量又是\(f(\frac{1}{2})\)，而一次性告诉你在D门，不确定性从\(\frac{1}{4}\)降到了\(1\)，信息量表示为\(f(\frac{1}{4})\)，也就是说

\[f(\frac{1}{4}) = f(\frac{1}{2}) + f(\frac{1}{2}) \]

而\(\frac{1}{4}\)这个概率来自概率\(\frac{1}{2} \times \frac{1}{2}\)，也就是信息量还要满足

\[f(\frac{1}{2} \times \frac{1}{2}) = f(\frac{1}{2}) + f(\frac{1}{2}) \]

因此便定义信息量：直观上理解为一个事件的不确定性程度

\[f(x) := -\log_{2}{x} \]

熵：信息量的期望，直观上理解为一个系统的不确定性程度

相对熵（KL散度）：直观上用来衡量两个系统的概率分布的差距

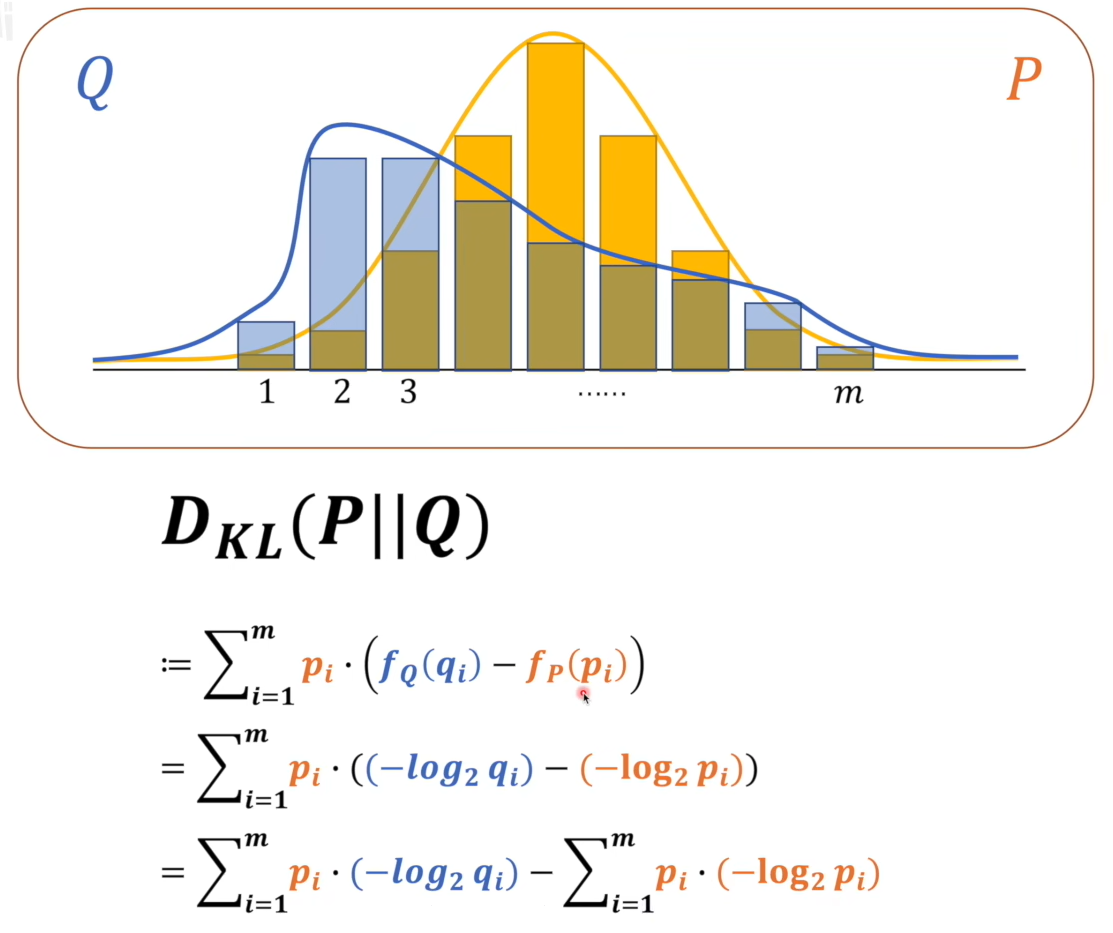
这个图一上来加上直观理解我们马上就可以联想到了多分类问题了，图中P在前面表示以P为基准来衡量Q，吉布斯不等式可以证明相对熵是大于等于0的，相对熵越大Q与P差距越大，这不就可以当损失函数了吗？因为在分类问题的标签中是其他值的概率为0（one-hot），所以后一项恒等于0，那我们的交叉熵损失就是前面那一项了

交叉熵损失：

\[Loss = \sum_{i=1}^{n} p_i(-\log_{2}{q_i}) \]

其中n是分类数，p是真实概率，q是网络的预测概率
设r是正确的那一类那么实际上交叉熵损失就是

\[Loss = p_r(-\log_{2}{q_r}) = -\log_{2}{q_r} \]

🔼返回顶部

---

在torch中的交叉熵损失似乎是用的ln函数，验证如下

a = torch.tensor([0, 1]).long()
b = torch.tensor([[1,1.0],
                  [11, 11]])
c = torch.nn.functional.cross_entropy(b,a)

这里b经过softmax后得出概率都是0.5，target a 指定第一个预测答案是1，第二个预测答案是2，结果

\[c = (-\ln \frac{1}{2} + -\ln \frac{1}{2}) / 2 = 0.6931 \]

🔼返回顶部

---