神经网络的理解
神经网络
目录
感知机
感知机是在很早之前提出来的现代神经网络的雏形,当时提出的时候引起了很大的关注,那么他有什么特性能够让人们关注它呢?
首先我们要知道感知机解决的问题,二分类问题。对于二维平面我们可以画条线将两类点分开,对于三维是一个平面,而对于更高的维度也同理。
下面以二维为例子,图上的所有点是输入给感知机的数据,颜色代表他们的分类,开始时假设感知机的直线就是 \(y = 0\) 而随着输入数据的增加我们可以不断调整感知机的参数使得让其能够完美分类图上的点,图中方程为 \(3x + 4b - 5 = 0\) (而感知机的线性层就是一个函数 \(3x + 4b - 5 = y\) ),而分类是用激活函数,显然线性层中 \(y>0\) 是一类 \(y<0\) 是另一类,所以说感知机的数学公式如下:
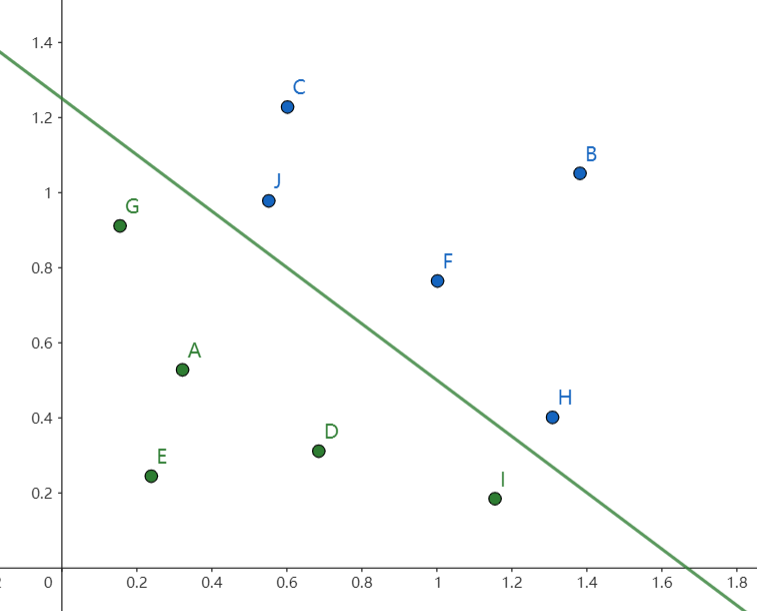
也就是说不论输入是多少个,不理论具体的分类规则有多详细,只要将数据输入给感知机,经过训练后就能得出最终的分类规则,也许就是感知机的这种模板性、通用性引起了人们的关注。
但是,不久后就有人提出感知机没法对异或进行分类,这一问题的发现使得感知机没落了几十年。
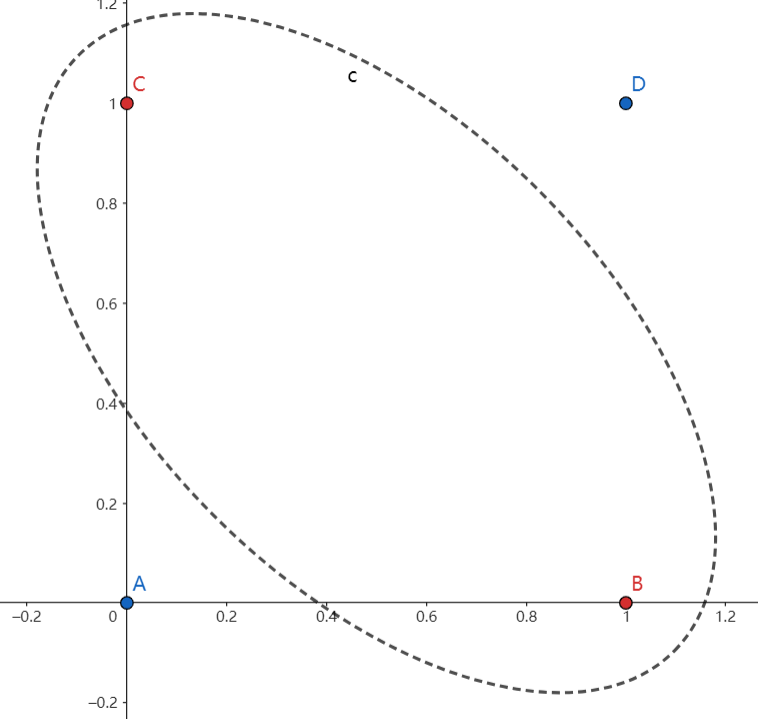
既然现在神经网络如此流行,那么肯定找出了解决方法。
-
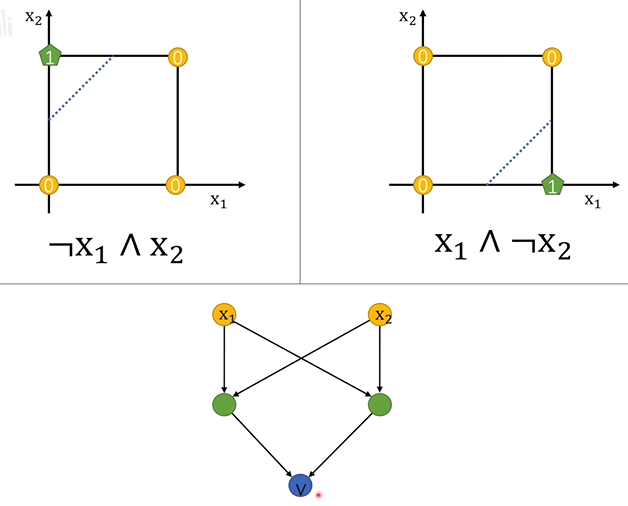
多个感知机嵌套,将两个感知机的输入输入到第三个感知机,确实解决了抑或问题,而且每层感知机还是线性层加上激活函数,也开始看到了现在网络的雏形。
-
升维,这种方法是在数据输入到的神经网络做一个变换,具体肯定要在感知机前面加一层
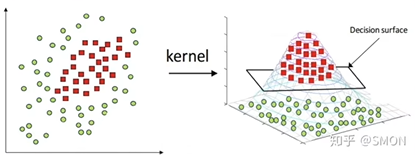
多层感知机
在感知机中我们讲了将多个感知机叠加就可以解决异或问题,那么有研究表明,只要神经网络含有隐藏层他就可以逼近任何函数。
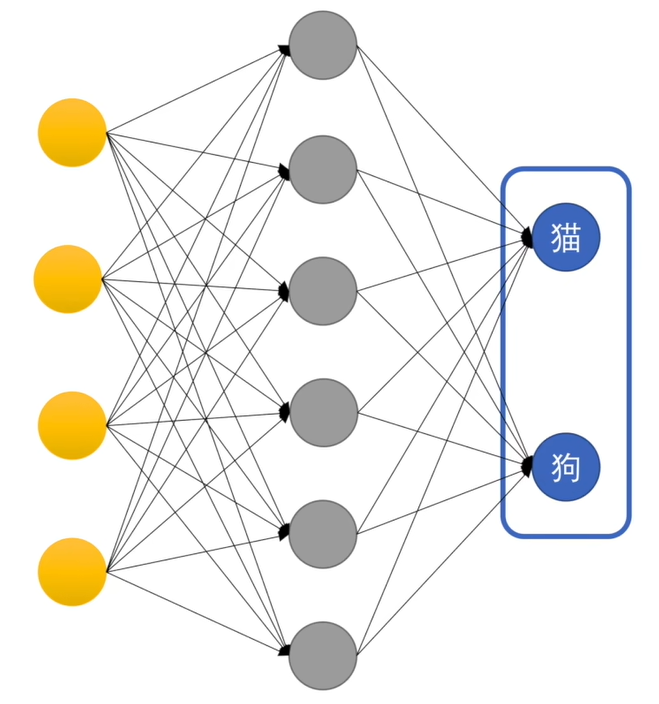
图中黄色部分是输入,灰色是一层感知机也是隐藏层,蓝色又是一层感知机也叫输出层。图中的神经网络做了二分类,当然也可以进行多分类。
如何理解多层感知机可以判断复杂的问题?我们知道感知机是在做一个二分类的问题,那么多层感知机就像是对输入的数据做出多次提问,让后将提问又输入给下一层接着问,再不断地逼问中最终确定是不是。而神经网络具体问的是什么问题,我们不得而知,这是在训练过程中网络自己总结的经验。
在多层感知机中激活函数不再是简单的阶跃函数,而是变成了具有平滑度的函数,这就意味着询问过程不再是简单的是不是,而是是的程度是多少,就成为了一个概率的问题,最后在集合了众多可能性之后做出最终判断。
如何理解训练出来的模型?可以将训练结果看作是泛化的猫和狗的样子,在理想世界可能存在一个最泛化的猫或狗的模型,而神经网络训练出来的模型要去逼近这个理想模型。
损失函数
我们在多层感知机里提到了如何去理解神经网络训练出来的模型,那么我们应该如何评估一个模型对理想模型的逼近程度,也就是好坏呢?
这就是损失函数存在的意义,损失函数越小意味着我们的模型越接近理想。
那么损失函数是怎么设计出来的呢?
梯度下降
损失函数是我们衡量模型质量的一个指标,那么如何让损失函数变小呢?
我们知道梯度指向的是函数增长速度最快的方向,对于损失函数这整个计算过程,所有神经元的权重和偏置都是变量,对所有这些参数求偏导得出的值就是损失函数值上升的方向,如果加上这个数值损失函数就会更大,减去这个数值,损失函数就会减小,我们只要求出所有参数的偏导并减去它们就可以使损失函数减小了。
学习率就是在下坡的方向上走多长的距离,学习率过大可能会越过极小值点,学习率过小学习会很慢。
我们不得不考虑一个问题,神经网络的参数初始是随机的,进行梯度下降我们得出的最终结果是一个局部最小值,并不是最优解,为什么可以呢?事实证明即使是局部最小值神经网络也可以出色的完成任务。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号